
第三章 化学平衡在滴定分析法中的应用 滴定分析法是滴定剂与被测组分反应,按反应类 型分为两大类: 生成反应 沉淀,配合物 转移反应 质子,电子 涉及的平衡问题:滴定曲线,滴定误差,滴定突跃, 可行性判据 §3-1生成反应型的滴定 T+D.K-TD (省去电荷) 滴定剂 被测物 TD K=月 络合滴定 [T][D]= 沉淀滴定 K
第三章 化学平衡在滴定分析法中的应用 化学平衡在滴定分析法中的应用 滴定分析法是滴定剂与被测组分反应,按反应类 型分为两大类: 生成反应 沉淀,配合物 转移反应 质子,电子 涉及的平衡问题:滴定曲线,滴定误差,滴定突跃, 可行性判据 §3-1 生成反应型的滴定 T + D TD (省去电荷) Kt 滴定剂 被测物 沉淀滴定 络合滴定 sp t t 1 1 [T][D] [T][D] [TD] K K K = = = = β

一滴定曲线 pT(或pD)~0(滴定分数)的关系曲线 0= np 滴定剂初始浓度c,加入体积 被测物初始浓度c。,体积o。 通常在理论分析时令c4=c,则0= 滴定至任一点 g92 c40 Cr=V+Vo 1+0 CD= V+Vo 1+0
一 .滴定曲线 pT (或 pD) ~ θ(滴定分数)的关系曲线 D T n n θ = 滴定剂初始浓度 0Tc ,加入体积 V; 被测物初始浓度 0Dc ,体积 V0。 通常在理论分析时令 0 0 D 0 T , V V c = c 则θ = 滴定至任一点 θ θ+ = + = 1 0T 0 0T T c V V c V c +θ = + = 1 0 D 0 0 0 D D c V V c V c

当TD是配合物 er [T]+[TD] cp [D]+[TD] 当TD是沉淀 c=T]+ nTD V+Vo co=[D]+-"D V+Vo 因此cr-co=T]-[D]
当 TD 是配合物 [ ] [ ] [ ] [ ] c D TD c T TD D T = + = + 当 TD 是沉淀 0 0 [ ] [ ] V V n c D V V n c T TD D TD T + = + + = + 因此 c cD [ D T] [ ] T − = −

当0>[T] D1=c-G,=c6-9-80-0 1+0 1+0 当8>1时,T]>D] m=g-cn-0-0-n 1+0 1+0 当0=1时,[T]=[D] 根据平衡常数的关系式,[T]、[D]相互换算, 即可作出pT(pD)~B的曲线
当θ > [T] θ θ θ θ + − = + − = − = 1 (1 ) 1 [D] 0 D 0 T 0 D D T c c c c c 当θ > 1 时,[T] >> [D] θ θ θ θ + − = + − = − = 1 ( 1) 1 [T] 0 T 0 D 0 T T D c c c c c 当θ = 1 时,[T] = [D] 根据平衡常数的关系式, [T]、[D]相互换算, 即可作出 pT (pD) ~ θ 的曲线

(例〉0.1 mol/L AgNO滴定0.1mo/L NaCl,计算0=0.1,0.5, 1,1.5时pAg。 c-0-0 解: 0<1 [CI]= 1+0 0=0.1 [CI]= 0.1X1-0.1) =0.082 1+0.1 [Ag]= K23209 =3.9×09 [ci] 0.082 pAg=8.41 0=05 pAg=8.01 0=1 [Ag"]=[CI ]=Ksp pAg2Pkp2949=474 1 0=1.5 [Ag']= £9-D_01X15-D=0.02 1+0 1+1.5 pAg=1.70
1.70 0.02 1 1.5 0.1 (1.5 1) 1 ( 1) 1.5 [ ] 0 = = + × − = + − = = + + pAg c Ag Ag θ θ θ 〈例〉0.1 mol/L AgNO3滴定0.1 mol/L NaCl,计算θ = 0.1, 0.5, 1, 1.5时pAg。 9.49 4.74 2 1 2 1 1 [ ] [ ] = = × = = = = + − sp sp pAg pK θ Ag Cl K 0.5 8.01 8.41 3.9 10 0.082 3.2 10 [ ] [ ] 0.082 1 0.1 0.1 (1 0.1) 0.1 [ ] 1 (1 ) 1 [ ] 9 10 0 = = = = × × = = = + × − = = + − < = − − − + − − − pAg pAg Cl K Ag Cl c Cl sp Cl θ θ θ θ 解: θ
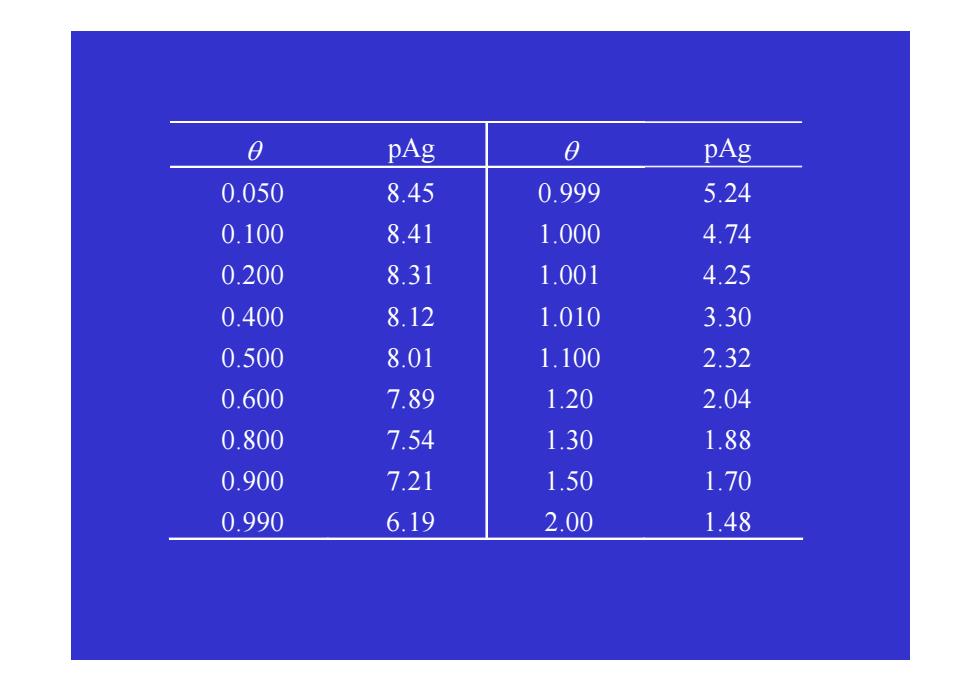
a pAg a pAg 0.050 8.45 0.999 5.24 0.100 8.41 1.000 4.74 0.200 8.31 1.001 4.25 0.400 8.12 1.010 3.30 0.500 8.01 1.100 2.32 0.600 7.89 1.20 2.04 0.800 7.54 1.30 1.88 0.900 7.21 1.50 1.70 0.990 6.19 2.00 1.48
θ pAg θ pAg 0.050 8.45 0.999 5.24 0.100 8.41 1.000 4.74 0.200 8.31 1.001 4.25 0.400 8.12 1.010 3.30 0.500 8.01 1.100 2.32 0.600 7.89 1.20 2.04 0.800 7.54 1.30 1.88 0.900 7.21 1.50 1.70 0.990 6.19 2.00 1.48
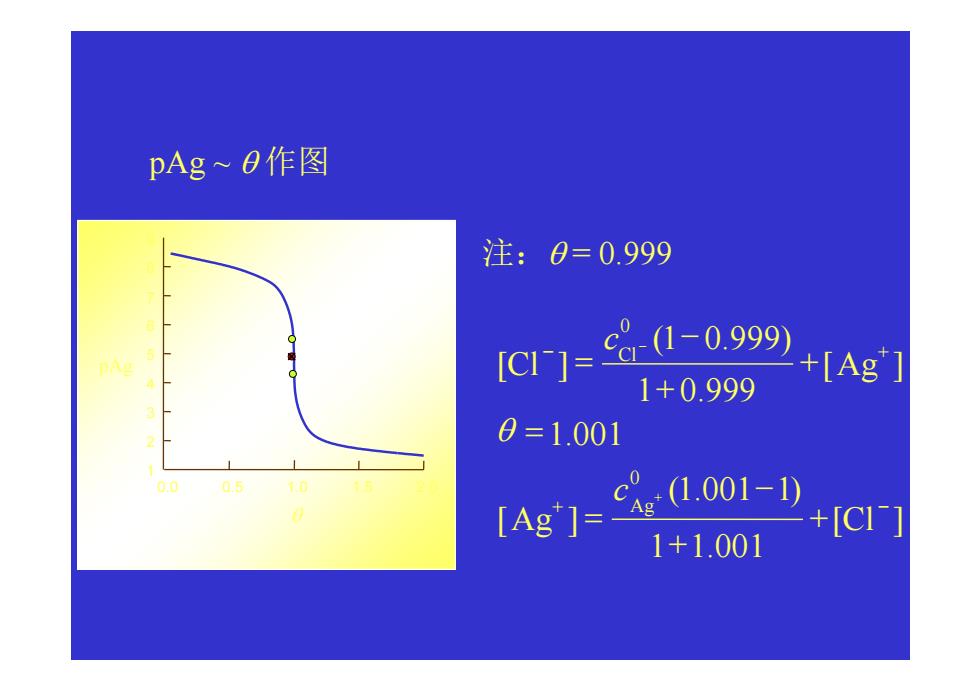
pAg~B作图 注:0=0.999 [C1]= 8-1-0.999 +[Ag] 1+0.999 0=1.001 (Ag'7=101- +[C1j 1+1.001
pAg ~ θ 作图 注:θ = 0.999 1+1.001 [ ] (1.001 1) [ ] 1.001 [ ] 1 0.999 (1 0.999) [ ] 0 0 + − − + + − = = + + − = + − Cl c Ag Ag c Cl Ag Cl θ 0.0 0.5 1.0 1.5 2.0 1 2 3 4 5 6 7 8 9 pAg θ

(例)pH=12,c&。=c=0.02mo/L时Y滴定Ca2, 计算0=0.5,1.0,1.5时的pCa。 解:无副反应,Ca+Y=CaY Ig B=10.7 0=05 Ca”1=80-0-002X0-05=667a0 1+0 1+0.5 pCa=2.18 0=1.0 [Ca2*]=[Y],[CaY]=Cca.eo =0.01 [Ca2] [CaY] 0.01 V100.7 =447107 pCa=6.35 或 ca=gB+0)=07+2)=635
〈例〉pH = 12, 0 0 Ca Y c = c = 0.02 mol/L 时 Y 滴定 Ca2+, 计算θ = 0.5, 1.0, 1.5 时的 pCa。 解:无副反应,Ca + Y CaY lg β = 10.7 (10.7 2) 6.35 21 (lg ) 21 6.35 4.47 10 10 [ ] 0.01 [ ] 1.0 [ ] [ ], [ ] 0.01 2.18 6.67 10 1 0.5 0.02 (1 0.5) 1 (1 ) 0.5 [ ] 7 10.7 2 . 2 3 0 2 = + = + = = = = = × = = = = = = × + × − = + − = = + − + + − pCa pC pCa CaY Ca Ca Y CaY c pCa c Ca eq CaY Ca eq Ca β β θ θ θ θ 或
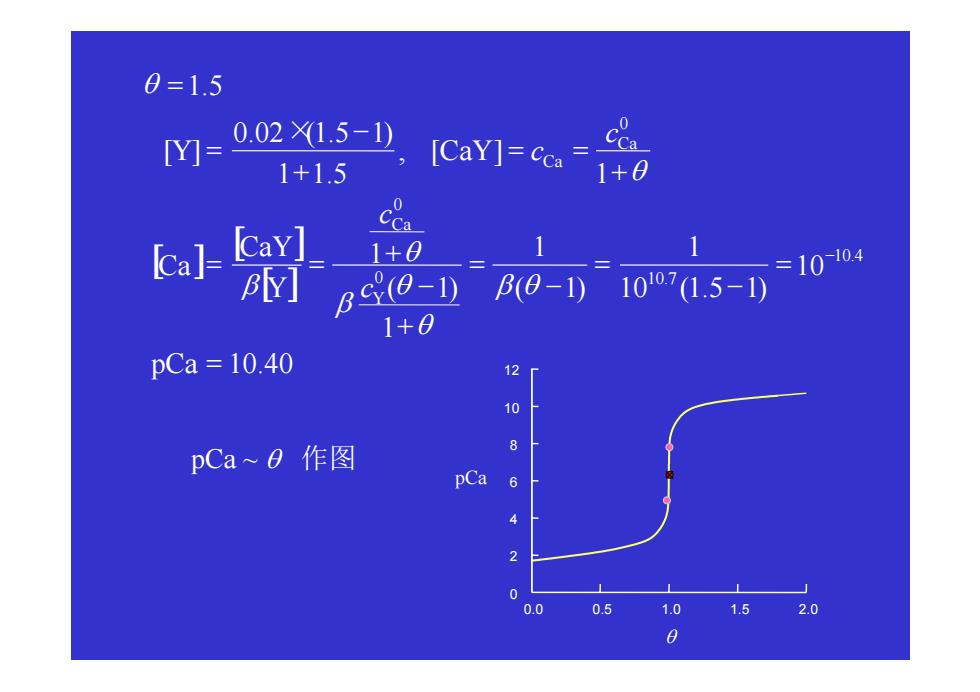
0=1.5 Y]= 0.021.5-) 1+1.5 ICaYl=co0 CCa a]上 CaY] 1+0 BY] Bs0- P0-1)10715-1) =10-104 1+0 pCa=10.40 12 10 pCa~o作图 8 pCa 6 2 0 0.0 0.5 1.0 1.5 2.0 0
[ ] [ ] [ ] 10.40 10 10 (1.5 1) 1 ( 1) 1 1 ( 1) 1 1 , [ ] 1 1.5 0.02 (1.5 1) [ ] 1.5 10.4 0 10.7 0 0 = = − = − = + − + = = + = = + × − = = − pCa c c Y CaY Ca c Y CaY c Y Ca Ca Ca β θ θ θ β θ β θ θ pCa ~ θ 作图 0.0 0.5 1.0 1.5 2.0 0 2 4 6 8 10 12 pCa θ

二.滴定误差与滴定突跃 1.滴定误差:终点与化学计量点不一致所引起的误差 TE=. iVep-CBVo c 分子、分母均除以Vep+o,由于cT=cpW+'p) TE=Cr.ep 二Cp.ep CD.ep 因为CpCp.sp=T]p-[D]p,则 E=2D2 计算误差的出发点 CD.ep
二.滴定误差与滴定突跃 1.滴定误差:终点与化学计量点不一致所引起的误差 0 0 0 0 c V c V c V TE D T ep D o − = 分子、分母均除以 Vep + V0,由于 ( ) 0 0 0 c V cep V Vep = + D ep T ep D ep c c c TE , , , − = 因为 c T ep c D ep T ep D ep [ ] [ ] , , − = − ,则 D ep ep ep c T D TE , [ ] − [ ] = 计算误差的出发点