
第三章 热力学第二定律 不可能把热从低温物 体传到高温物体,而 不引起其它变化 Clausius The Second Law of Termodynantics
第三章 热力学第二定律 不可能把热从低温物 体传到高温物体,而 不引起其它变化 Clausius

3.1 热力学第二定律 Second law of thermodynamics 3.1.1.自发过程 自然界中任一孤立系统中,不论发生什么变 化,变化前后的内能总和不变;但是不是任何内 能总和保持不变的任何变化,均能在孤立系统中 发生。 自然界中实际发生的一切变化,即自发过程 (spantaneous process),都不会在原来发生变化影响 所及的各物体所组成的孤立系统中反过来进行
3.1.1.自发过程 Second law of thermodynamics 3.1 热力学第二定律 自然界中任一孤立系统中,不论发生什么变 化,变化前后的内能总和不变;但是不是任何内 能总和保持不变的任何变化,均能在孤立系统中 发生。 自然界中实际发生的一切变化,即自发过程 (spantaneous process),都不会在原来发生变化影响 所及的各物体所组成的 孤立系统中反过来进行

自然界中任一孤立系统中所实际发生 了的变化,如果引入另外的物体加入这一弧 立系统,则原来的变化,一般可以复原,但 却引起了新引进物体的变化。这个新引进的 变化。当然还可以引进又一组新物体,使它 复原,但这又一组新物体又将发生变化。 自然界中任一孤立系统中所实际发生的 变化,都是不可逆变化,与不可逆变化的方向 相反的变化,在原弧立系统中永远不可能发 生
自然界中任—孤立系统中所实际发生 了的变化,如果引入另外的物体加入这一弧 立系统,则原来的变化,一般可以复原,但 却引起了新引进物体的变化。这个新引进的 变化。当然还可以引进又一组新物体,使它 复原,但这又一组新物体又将发生变化。 自然界中任一孤立系统中所实际发生的 变化,都是不可逆变化,与不可逆变化的方向 相反的变化,在原弧立系统中永远不可能发 生

自发变化的共同特征 自发变化某种变化有自动发生的趋势,一旦发生就 无需借助外力,可以自动进行,这种变化称为自发变 化 自发变化的共同特征一不可逆性任何自发变化的逆 过程是不能自动进行的。例如: (1) 焦耳热功当量中功自动转变成热; (2) 气体向真空膨胀; (3) 热量从高温物体传入低温物体; (4) 浓度不等的溶液混合均匀; (5) 锌片与硫酸铜的置换反应等, 它们的逆过程都不能自动进行。当借助外力,体系恢复 原状后,会给环境留下不可磨灭的影响
自发变化的共同特征 自发变化 某种变化有自动发生的趋势,一旦发生就 无需借助外力,可以自动进行,这种变化称为自发变 化。 自发变化的共同特征 —不可逆性 任何自发变化的逆 过程是不能自动进行的。例如: (1) 焦耳热功当量中功自动转变成热; (2) 气体向真空膨胀; (3) 热量从高温物体传入低温物体; (4) 浓度不等的溶液混合均匀; (5) 锌片与硫酸铜的置换反应等, 它们的逆过程都不能自动进行。当借助外力,体系恢复 原状后,会给环境留下不可磨灭的影响

3.1.2热力学第二定律的文字表述 克劳修斯(Clausius)说法: 不可能把热由低温物体传到高温物体,而 不引起其他变化。” 开尔文(Kelvin)说法: 不可能从单一热源取出热使之完全转化为 功,而不发生其它变化。 第二类永动机是不可能的。(从单一热源吸热使 之完全变为功而不留下任何影响。)
3.1.2 热力学第二定律的文字表述 克劳修斯(Clausius)说法: “不可能把热由低温物体传到高温物体,而 不引起其他变化。” 开尔文(Kelvin)说法: “不可能从单一热源取出热使之完全转化为 功,而不发生其它变化。” 第二类永动机是不可能的。(从单一热源吸热使 之完全变为功而不留下任何影响。 )

3.1.3热力学第二定律的数学式表述 热力学第一定律的本质为能量守恒原理:每 一物体都存在一状态函数称为热力学能函数U,在 孤立系统中。不管发生任何变化,各物体的热力 学能总和恒定不变。 ∑B△UB=0 热力学第二定律的本质为熵增加原理:每一 物体都存在一状态函数称为熵S。在孤立系统中, 不管发生任何变化,各物质的熵总和永不降低。 ∑B△SB≥0
3.1.3 热力学第二定律的数学式表述 热力学第一定律的本质为能量守恒原理:每 一物体都存在一状态函数称为热力学能函数U,在 孤立系统中。不管发生任何变化,各物体的热力 学能总和恒定不变。 ∑B △UB=0 热力学第二定律的本质为熵增加原理:每一 物体都存在一状态函数称为熵S 。 在孤立系统中, 不管发生任何变化,各物质的熵总和永不降低。 ∑B△SB≥0
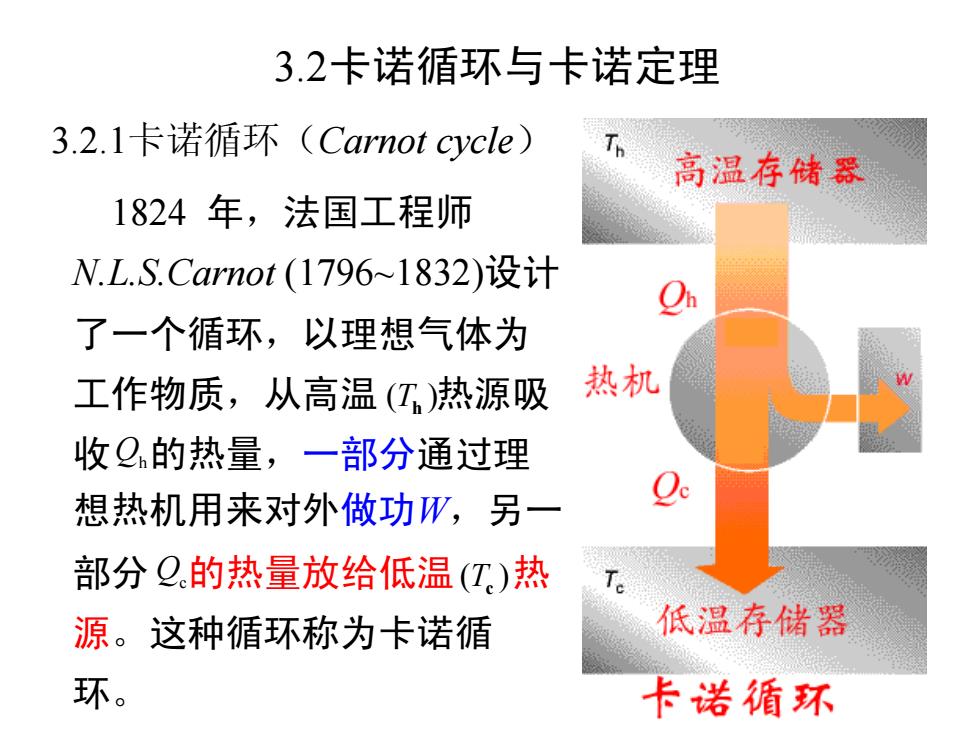
3.2卡诺循环与卡诺定理 3.2.1卡诺循环(Carnot cycle) 高温存储器 1824年,法国工程师 N.L.S.Carnot(1796~1832)设计 了一个循环,以理想气体为 工作物质,从高温(工)热源吸 热机 收Q的热量,一部分通过理 想热机用来对外做功W,另一 部分Q的热量放给低温(T)热 源。这种循环称为卡诺循 低温存储器 环。 卡诺循环
3.2卡诺循环与卡诺定理 3.2.1卡诺循环(Carnot cycle) 1824 年,法国工程师 N.L.S.Carnot (1796~1832)设计 了一个循环,以理想气体为 工作物质,从高温 热源吸 收 的热量,一部分通过理 想热机用来对外做功W,另一 部分 的热量放给低温 热 源。这种循环称为卡诺循 环。 ( ) Th Qh Qc ( ) Tc
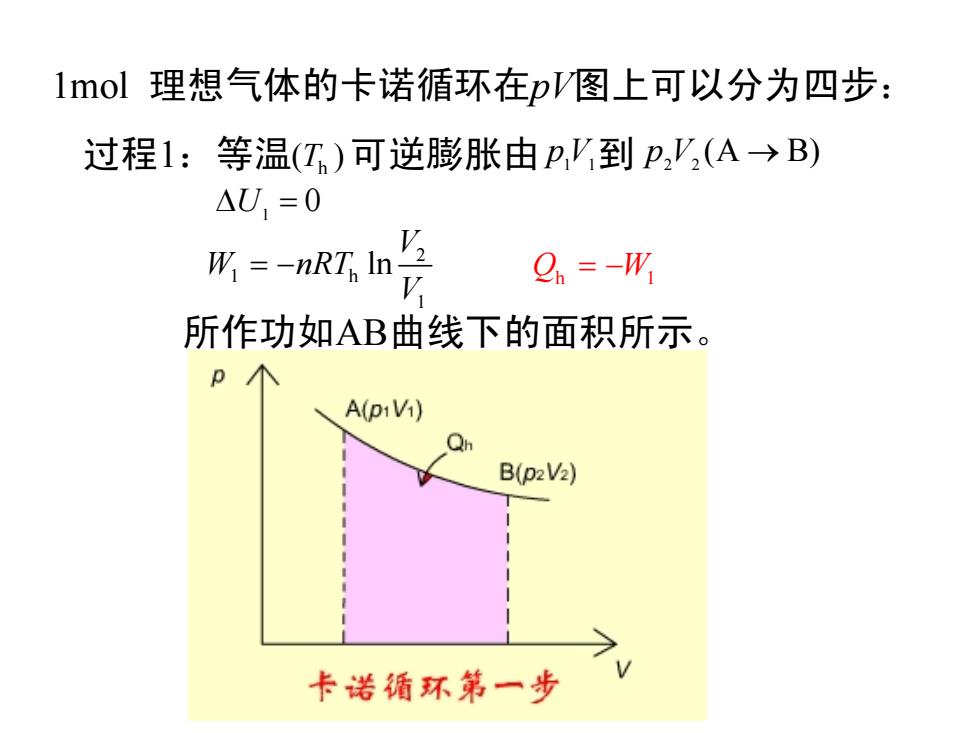
lmol理想气体的卡诺循环在pV图上可以分为四步: 过程1:等温(T)可逆膨胀由p,V到p,'(A→B) △U=0 形=-nRn点 Q.=-W 所作功如AB曲线下的面积所示。 A(piVi) B(p2V2) 卡诺循环第一步
1mol 理想气体的卡诺循环在pV图上可以分为四步: 过程1:等温( ) Th 可逆膨胀由 p1V1到 (A B) p2V2 → 0 ∆U1 = 2 1 h 1 ln V W nRT V = − 所作功如AB曲线下的面积所示。 Q W h 1 = −
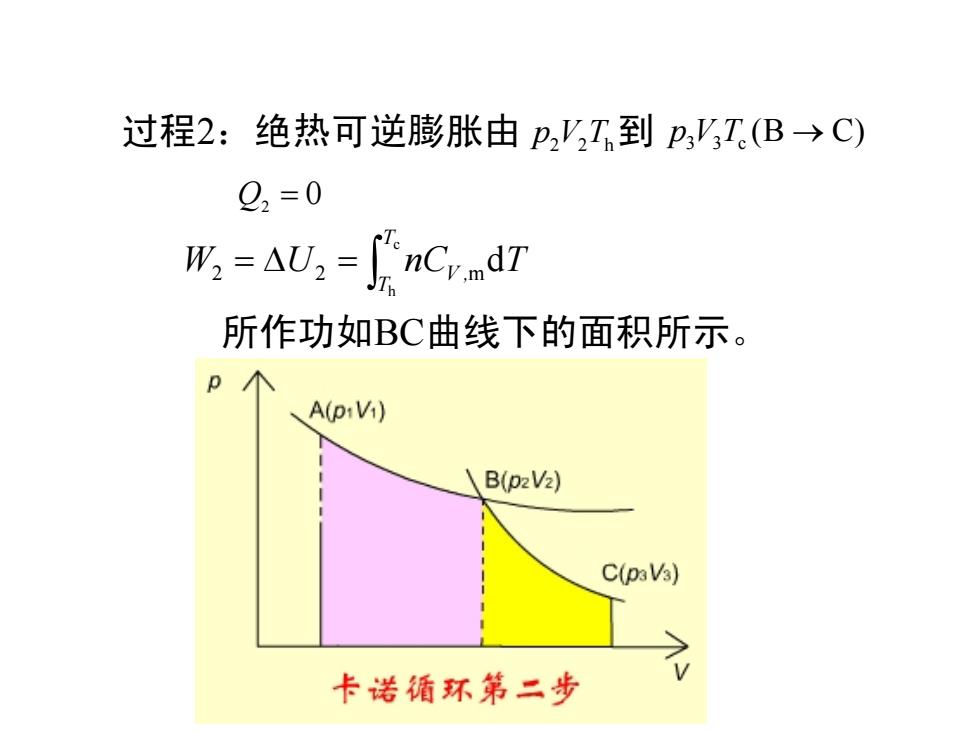
过程2:绝热可逆膨胀由p,V,I,到pVT(B→C) 92=0 所=A,=nCrndT 所作功如BC曲线下的面积所示。 A(piVi) B(p2V2) C(paVs) 卡诺循环第二步
过程2:绝热可逆膨胀由 p2 2 V Th到 3 3 c pVT (B → C) 0 Q2 = 所作功如BC曲线下的面积所示。 ∫ = ∆ = ch d 2 2 m TT W U nCV , T
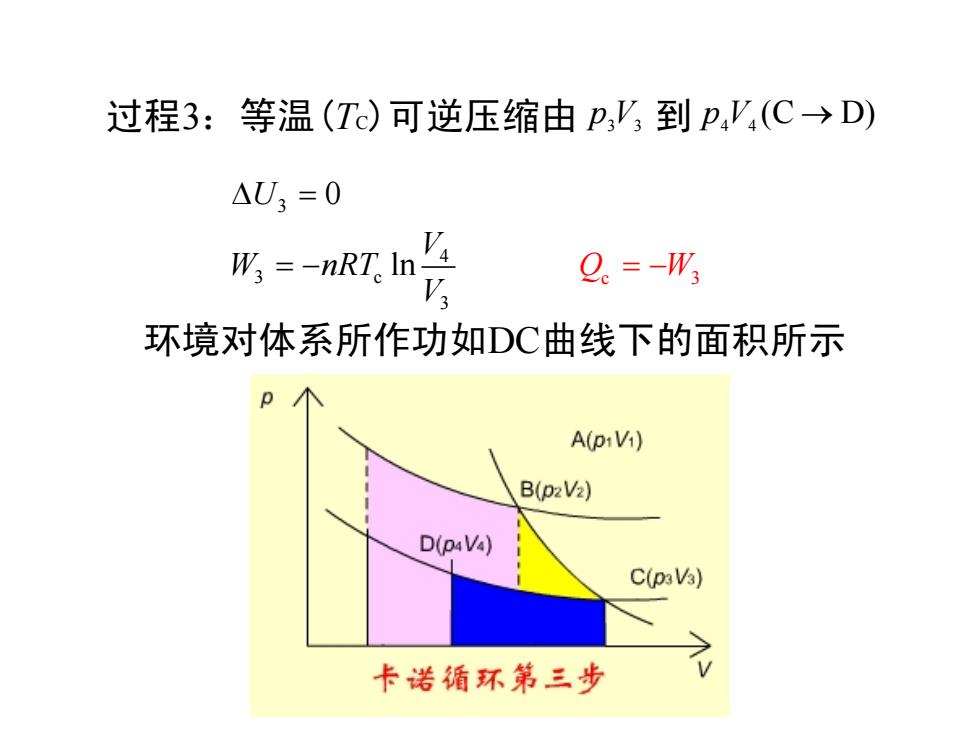
过程3:等温(Tc)可逆压缩由p,',到p'(C→D) △U3=0 W=-nRT。ln Q。=-W 环境对体系所作功如DC曲线下的面积所示 A(piVi) B(pzV2) D(p4Va) C(paVa) 卡诺循环第三步
过程3:等温(TC)可逆压缩由 p3V3 到 (C D) p4V4 → 3 4 3 c 3 0 ln U V W nRT V ∆ = = − 环境对体系所作功如DC曲线下的面积所示 Q W c 3 = −