
△G和△G在使用上的区别 在无机化学的学习中己经知道,严格地,必须用△G来判断 一个反应或一个过程的自发性。 △G=△G9+RTInQ,△G9=-RTInK, 当达到平衡时,其标志是△G=0,而不是△G=0(△G=0, 意味着K=1)。而且,只要反应的K1,达到平衡时,Q=K,此 时,Q≠1,RTInQ:0,即△G≠△G。 只有在极为特殊的情况下: ①标准态(Q=1), ②Q=(cC)/ccD/c9 (c(A)/c0)a(c(B)/c0)b =1(但不是标准态), 在这两种情况下,△G=-RTInK+RTInQ=△G+RTIn1= △G。这时,△G与△G才无区别。 因此,要用△G判断反应或过程的方向,必须在上述两种特殊 情况下进行,离开了这两种特殊情况而使用△G显然是不合适的
△G和△Gθ在使用上的区别 在无机化学的学习中已经知道,严格地,必须用△G来判断 一个反应或一个过程的自发性。 △G=△Gθ+RTlnQ, △Gθ=-RTlnK, 当达到平衡时,其标志是△G=0,而不是△Gθ=0(△Gθ=0, 意味着K=1)。而且,只要反应的K≠1,达到平衡时,Q=K,此 时,Q≠1,RTlnQ≠0,即△G≠△Gθ 。 只有在极为特殊的情况下: ①标准态(Q=1), ② Q= =1(但不是标准态), 在这两种情况下,△G=-RTlnK+RTlnQ=△Gθ+RTln1= △Gθ。这时,△G与△Gθ才无区别。 因此, 要用△Gθ判断反应或过程的方向, 必须在上述两种特殊 情况下进行, 离开了这两种特殊情况而使用△Gθ显然是不合适的。 (c(C)/c θ ) c (c(D)/c θ ) d (c(A)/c θ ) a (c(B)/c θ ) b

除了上述两种情况之外,就必须使用△G。 △G=△G+RTInQ=-RTInK+RTInQ=RTInQ/K 可见△G的值和符号,全取决于Q与K的值。 当 Q/K>1,Q>K,△G>0, Q/K<1,Q<K,△G<0, Q/K=1,Q=K,△G=0, 这样一来,Q对K的比值,从而也就是△G的大小和符号表 征了体系在除上述两种特殊情况之外的任意状态离平衡状态有多 远
除了上述两种情况之外,就必须使用△G。 △G=△Gθ+RTlnQ=-RTlnK+RTlnQ=RTlnQ/K 可见△G的值和符号,全取决于Q与K的值。 当 Q/K >1, Q>K, △G>0, Q/K <1, Q<K, △G<0, Q/K=1, Q=K, △G=0, 这样一来,Q对K的比值,从而也就是△G的大小和符号表 征了体系在除上述两种特殊情况之外的任意状态离平衡状态有多 远

如,对于一个反应 Zn+Cu2+→Zn2++Cu 在通常使用标准电极电势或标准电动势去进行判断时 E0(Zn2+/Zn)0 标准电极电势E上面的“”,意指(Zn2+)=(Cu2+)=1mol1-1 的情形,此时 Q= (Zn2+)/c9 (Cu2+)/c9 -=1,()为任一时刻的浓度。 反应的平衡常数 [Zn2+]/c9 [Cu2+]/c0 -=1037,[]为平衡浓度。 AGO=-2FE0=-RTInK =-211.078 kJ.mol-10w时,或Q>K, △G>0,逆向为自发,即铜置换锌便是自发的了(然而在这种情况 下,其标准电动势E仍大于0,△G仍小于0)
如,对于一个反应 Zn+Cu2+ Zn2++Cu 在通常使用标准电极电势或标准电动势去进行判断时 E θ (Zn2+/Zn) 0 标准电极电势E θ上面的“θ”,意指(Zn2+)=(Cu2+)=1mol·l-1 的情形,此时 Q= =1,( )为任一时刻的浓度。 反应的平衡常数 =1037 ,[ ]为平衡浓度。 △Gθ=-2FEθ=-RTlnK =-211.078 kJ·mol-11037时,或Q>>K, △G>0, 逆向为自发,即铜置换锌便是自发的了(然而在这种情况 下,其标准电动势 E θ仍大于0,△Gθ仍小于0)。 (Zn2+)/c θ (Cu2+)/c θ [Zn2+]/c θ [Cu2+]/c θ (Zn2+)/c θ (Cu2+)/c θ (Zn2+)/c θ (Cu2+)/c θ

由此可见,反应的自发性是和体系中各物质的起始分压或起 始浓度有关的,除了指定是上述两种特定状态可用△G去判断方 向以外,其它状态都必须使用△G去判断。 事实上,由等温方程可见△G=△G+RTnQ,对于一个给定 反应,△G是一个定值,但却可以通过调节Q值来改变△G的大小 和符号。换句话说,起始分压或浓度可以确定△G的大小和符号, 从而确定反应的自发方向。 再如: CaSO-Ca2+(aq)+SO2-(aq), Kp9-[Ca2+][S0,2-]/(cy2=9.1X10-6 AGO-RTInKsp0=28.7 kJmol-1>0 表明在标准状态下,即(Ca2+)和(S0,2-)均为1molL-1时, CaSO4的溶解是非自发的;相反,其逆过程亦即1molL-l的Ca2+ 和1molL-1的SO2-遇到一起发生沉淀却是自发的(逆过程的△G9 =一28.7 kJ.mol-1<0),这完全符合事实,这时沉淀过程将一直进 行到固液相达到平衡,亦即离子浓度积减小到等于K时为止。如 果溶液中起始离子浓度积比Kp还要小,则△G=RTInQ/KpcO,必 将引起自发的溶解,直到建立新的固液平衡,△G=0为止
由此可见,反应的自发性是和体系中各物质的起始分压或起 始浓度有关的,除了指定是上述两种特定状态可用△Gθ去判断方 向以外,其它状态都必须使用△G去判断。 事实上,由等温方程可见△G=△Gθ+RTlnQ,对于一个给定 反应,△Gθ是一个定值,但却可以通过调节Q值来改变△G的大小 和符号。换句话说,起始分压或浓度可以确定△G的大小和符号, 从而确定反应的自发方向。 再如: CaSO4 Ca2+(aq)+SO4 2-(aq), Ksp θ=[Ca2+][SO4 2-]/(cθ ) 2=9.1×10-6 △Gθ=-RTlnKsp θ=28.7 kJ·mol-1 > 0 表明在标准状态下, 即(Ca2 +)和(SO4 2-)均为1mol·L-1时, CaSO4的溶解是非自发的;相反,其逆过程亦即1 mol·L-1的Ca2+ 和1 mol·L-1的SO4 2-遇到一起发生沉淀却是自发的(逆过程的△Gθ =-28.7 kJ·mol-1< 0),这完全符合事实, 这时沉淀过程将一直进 行到固液相达到平衡,亦即离子浓度积减小到等于Ksp时为止。如 果溶液中起始离子浓度积比Ksp还要小,则△G=RTlnQ/Ksp θ< 0,必 将引起自发的溶解, 直到建立新的固液平衡,△G=0为止

对通常条件下的反应,亦即各物质的起始浓 度并非全处于标准状态时的反应,既然应该用△G 去判别其反应的自发性,而且这又需要知道各物 质的起始分压或起始浓度,这颇感不便。此外, 由热力学数据表中查得的热力学数据都是标准态 下的热力学数据,如果能用△G去代替△G进行判 别,那该是多么方便呀。于是人们就探讨在什么 样的情况下可以用△G代替△G来判别的问题
对通常条件下的反应,亦即各物质的起始浓 度并非全处于标准状态时的反应,既然应该用△G 去判别其反应的自发性,而且这又需要知道各物 质的起始分压或起始浓度,这颇感不便。此外, 由热力学数据表中查得的热力学数据都是标准态 下的热力学数据,如果能用△Gθ去代替△G进行判 别,那该是多么方便呀。于是人们就探讨在什么 样的情况下可以用△Gθ代替△G来判别的问题

若某反应,其△G负值很大,如等于一500 kJ-mol-1,则 -500×103 1gk=-2.303×8.314×29888,K=108>1 表明该反应达到平衡时,生成物远远多于反应物,其相差的 倍数已经达到了无法改变的程度,纵然是开始时该体系只有生成 物,但只要逆反应一进行,反应就很快达到平衡。如果体系中生成 物的浓度很大,但与反应物相比,其相差的倍数还不象K值那么 巨大,Q>1088,Q57, Q>K,△G>0。逆向反应反而是自发的,前面的判断便成了错误
若某反应,其△Gθ负值很大,如等于-500 kJ·mol-1,则 lgK=- ≈88,K=1088>>1 表明该反应达到平衡时,生成物远远多于反应物,其相差的 倍数已经达到了无法改变的程度,纵然是开始时该体系只有生成 物, 但只要逆反应一进行, 反应就很快达到平衡。如果体系中生成 物的浓度很大,但与反应物相比,其相差的倍数还不象K值那么 巨大,Q>1088 ,Q57, Q>K, △G > 0。逆向反应反而是自发的, 前面的判断便成了错误。 -500×103 2.303×8.314×298 -10×103 2.303×8.314×298

相反,若一反应的△G正值很大,则K值极小(K40 kJ.mol-1或 K>10?和K<10-7作为反应实际上是自发和非自发的判断依据; 而当一40<△G<40 kJ.mol-1、10-7<K<107时,用△G判别会带 来错误的可能,因为此时各物质的起始分压或浓度所起的作用 较大之故,此时,就应该用△G去判别反应的自发性
相反,若一反应的△Gθ正值很大,则K值极小(K 40 kJ·mol-1或 K>107和K<10-7作为反应实际上是自发和非自发的判断依据; 而当-40<△Gθ< 40 kJ·mol-1 、10-7<K<107时,用△Gθ判别会带 来错误的可能,因为此时各物质的起始分压或浓度所起的作用 较大之故,此时,就应该用△G去判别反应的自发性

焓变及熵变在△G中的贡献 根据吉布斯一吉姆霍斯方程△G=△H一T△S,可以发现,吉 布斯自由能变化包括两个方面的贡献,即焓变项和熵变项。 很显然,如果在反应过程中,熵变较小、或者是同类反应有 类似的熵变的话,显然可以用△H代替△G去判断反应的自发性。 根据方程式,如果△H与△S的符号相同,即都为正或都为负, 则焓变项和熵变项对自由能变化分别作出相反的贡献。但是,在 化学反应中,通常的熵变△只有几十到几百JK-1mol-1,而△H 通常为几十到几百kJmol-1。在298K时,3JK-1mol-1的熵变对 自由能的贡献小于1 kJ.mol-1的焓变对自由能的贡献(3J·K-1mol-1 ×298K=0.894 kJ.mol-)。这样一来,在低温时,△S不管是正 还是负,△G的符号总是由△H的符号来决定,因此,在低温时, 唯有放热反应(△H0→△G<0的过 程中,有一个△G=0的时刻,此时△H=T△S,T=△H/△S, 这个温度称为转折温度。过了这个温度,反应方向就逆转了
焓变及熵变在△G中的贡献 根据吉布斯—吉姆霍斯方程△G=△H-T△S,可以发现,吉 布斯自由能变化包括两个方面的贡献,即焓变项和熵变项。 很显然,如果在反应过程中,熵变较小、或者是同类反应有 类似的熵变的话,显然可以用△H代替△G去判断反应的自发性。 根据方程式,如果△H与△S的符号相同,即都为正或都为负, 则焓变项和熵变项对自由能变化分别作出相反的贡献。但是,在 化学反应中,通常的熵变△S只有几十到几百J·K-1·mol-1 ,而△H 通常为几十到几百kJ·mol-1 。在298K时,3 J·K-1·mol-1的熵变对 自由能的贡献小于1kJ·mol-1的焓变对自由能的贡献(3 J·K-1·mol-1 ×298 K=0.894 kJ·mol-1 )。这样一来,在低温时,△S不管是正 还是负,△G的符号总是由△H的符号来决定,因此,在低温时, 唯有放热反应(△H 0 △G < 0 的过 程中,有一个△G=0的时刻,此时△H=T△S,T=△H/△S, 这个温度称为转折温度。过了这个温度,反应方向就逆转了
下面列出几种化合物的标准生成焓和标准生成自由能。 化合物 S02 C02 FeS S03 S证4 MgO △Hme/kJ.mol-1 -297 -394 -95 -395 1548 -602 △Gm9/kJ.mol-1 -300 -395 98 -370 1506 -569 前三种化合物,由指定单质生成这些物种的过程中气态物 的摩尔数没有发生变化。如 C(S)+O2(g)→C02(g) △ng为0,△s变化很小,T△S项数值不大,所以△Hm与 △Gm值甚为接近, △H=△Hm≈△Gm9 而右边三种,由指定单质生成该物种时,气体物质的摩尔 数发生了变化,如 Si(s)+2F2 (g)SiF4(g) △ng=-1,熵变(减小)使得△Hm与△Gm相差较大,此时 △S<0,T△S<0,△G 尽管如此,焓变项数值仍然优势地超过了熵变项,△G的符 号由△H决定
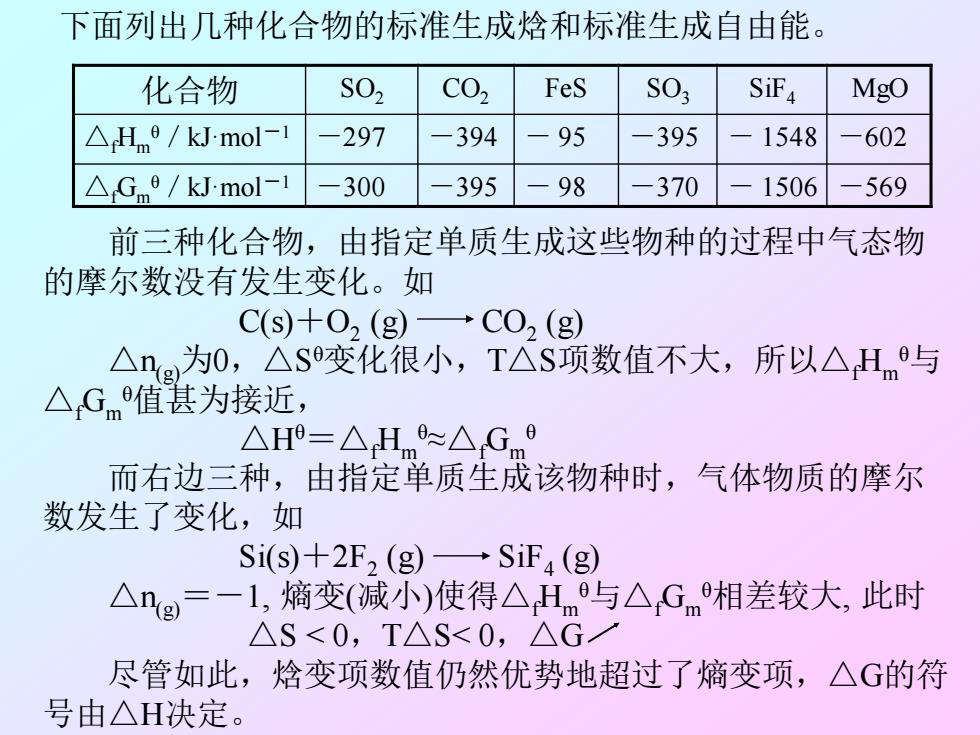
化合物 SO2 CO2 FeS SO3 SiF4 MgO △fHm θ/kJ·mol-1 -297 -394 - 95 -395 - 1548 -602 △fGm θ/kJ·mol-1 -300 -395 - 98 -370 - 1506 -569 下面列出几种化合物的标准生成焓和标准生成自由能。 前三种化合物,由指定单质生成这些物种的过程中气态物 的摩尔数没有发生变化。如 C(s)+O2 (g) CO2 (g) △n(g)为0,△S θ变化很小,T△S项数值不大,所以△fHm θ与 △fGm θ值甚为接近, △Hθ=△fHm θ≈△fGm θ 而右边三种,由指定单质生成该物种时,气体物质的摩尔 数发生了变化,如 Si(s)+2F2 (g) SiF4 (g) △n(g) =-1, 熵变(减小)使得△fHm θ与△fGm θ相差较大, 此时 △S < 0,T△S< 0,△G 尽管如此,焓变项数值仍然优势地超过了熵变项,△G的符 号由△H决定

如果反应有较大的熵变,特别是当温度有显著的改变时,△G 的符号就有可能由熵变项决定,如 NH CI(s)-NH3(g)+HCI(g) 反应进行时产生了气体物质,△ng=2,将伴随有明显的熵 增,△S=285J·K-1.mol-1,随着温度升高,△G将从大于0(= 21.2kJmo-)变为小于0。此时NH,C1(s)将发生自发分解。 △G=AH一8 一个相反的例子是2C0(g十C(sC02(g△ng=-1, △S=一176J·K-1·mol-1<0,反应为熵减,随着温度升高,△G9 从小于0(-120 kJ.mol-1)变为大于0。事实证明,当温度在700℃ 以上时,平衡混合物中以CO占优势,反应向逆方向进行。 若对相同类型的反应进行比较,可以发现熵变项对△G的影响 的重要性降低,此时只比较△H就可以了。如各种MCO,分解的熵 变几乎是相同的,分解反应的熵变与M无关,其热分解方式为: MCO:(s)-MO(s)+CO2(g) 在这种情况下,其分解的规律性一般就可以近似地用焓变的变 化规律来进行讨论
如果反应有较大的熵变, 特别是当温度有显著的改变时, △G 的符号就有可能由熵变项决定,如 NH4Cl(s) NH3 (g)+HCl(g) 反应进行时产生了气体物质,△n(g) =2,将伴随有明显的熵 增, △S θ=285 J·K-1·mol-1 ,随着温度升高,△Gθ将从大于0 (= 21.2 kJ·mol-1 )变为小于0。此时NH4Cl (s)将发生自发分解。 △G=△H-T△S 一个相反的例子是 2CO(g)+C(s) CO2 (g) △n(g) =-1, △S θ=-176 J·K-1·mol-1 0 高 >0 △ 若对相同类型的反应进行比较, 可以发现熵变项对△Gθ的影响 的重要性降低,此时只比较△H就可以了。如各种MCO3分解的熵 变几乎是相同的, 分解反应的熵变与M无关, 其热分解方式为: MCO3 (s) MO(s)+CO2 (g) 在这种情况下, 其分解的规律性一般就可以近似地用焓变的变 化规律来进行讨论