
对镧系元素氧化态的热力学讨论 1镧系元素十2氧化态的稳定性 以LX,的氧化反应为例: LnX2(s)+1/2X2(参考态)→LnX,(s)△Hm9 显然,反应的△Hm的绝对值越大,LnX(s)越稳定。 写出这个反应的玻恩一哈伯热化学循环: LnX,S十12X,(参考态)△L°LnX,(S L △Hm(X-,g 12 Lm2+(g十千2X-(g+X-(g5Ln+(g)十3X-(g 由此有△Hm=L3+L1一L2+△Hm(X-,g) 式中I3为镧系元素的第三电离能,L1、L2分别是LX2(S)、 LnX3(s的晶格能,对于同一类型的反应,△Hm(X-,g)为常数, 熵变也认为是常数,因此,反应的Gibbs自由能变可写为: △,Gm≈△HmA=L3十L1-L2+常数
对镧系元素氧化态的热力学讨论 1 镧系元素+2氧化态的稳定性 以LnX2的氧化反应为例: LnX2 (s)+1/2 X2 (参考态) → LnX3 (s) △rHm θ 显然,反应的△rHm θ的绝对值越大,LnX2 (s)越稳定。 写出这个反应的玻恩-哈伯热化学循环: 式中I3为镧系元素的第三电离能,L1、L2分别是LnX2 (s)、 LnX3 (s)的晶格能,对于同一类型的反应,△fHm θ (X-,g)为常数, 熵变也认为是常数,因此,反应的Gibbs自由能变可写为: △rGm θ≈△rHm θ=I3+L1-L2+常数 LnX2 (s)+1/2 X2 (参考态) ———→ LnX3 (s) Ln2+(g)+2X-(g)+X-(g) ——→ Ln3+(g)+3X-(g) L1 △fHm L2 θ (X-,g) I3 △rHm θ 由此有 △rHm θ=I3+L1-L2+ △fHm θ (X-,g)
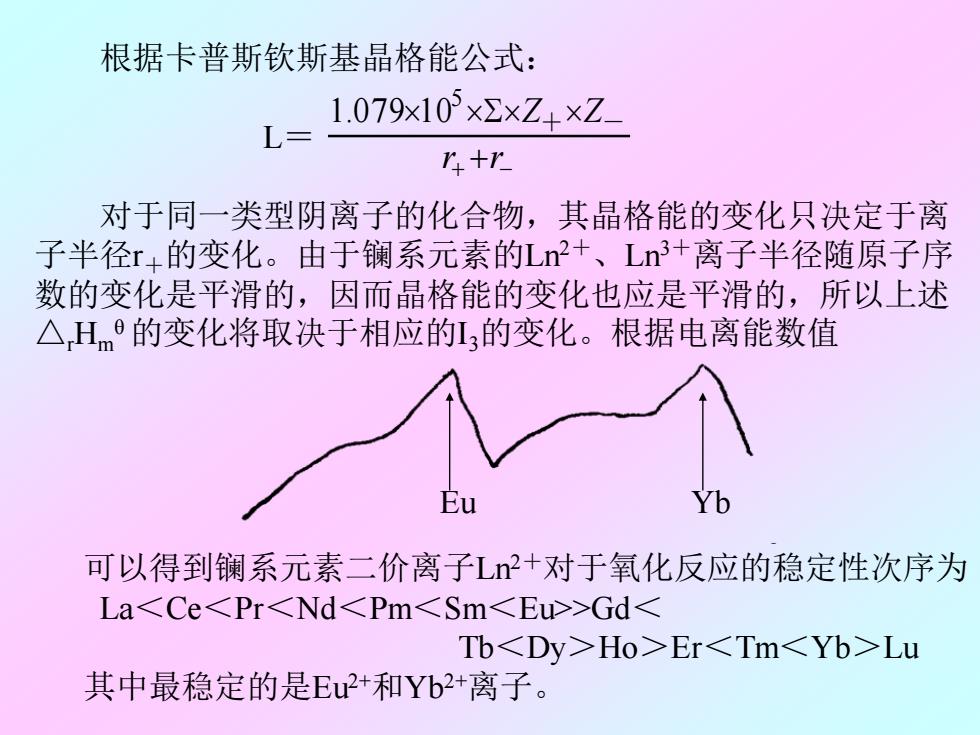
根据卡普斯钦斯基晶格能公式: 1.079x103×2×Z+×Z_ L三 八+r 对于同一类型阴离子的化合物,其晶格能的变化只决定于离 子半径r+的变化。由于镧系元素的Ln2+、Ln3+离子半径随原子序 数的变化是平滑的,因而晶格能的变化也应是平滑的,所以上述 △Hm9的变化将取决于相应的13的变化。根据电离能数值 Yb 可以得到镧系元素二价离子L+对于氧化反应的稳定性次序为 La>GdHo>ErLu 其中最稳定的是Eu2+和Yb2+离子
+ + − r r Z + Z - 5 1.079 1 0 根据卡普斯钦斯基晶格能公式: L= 对于同一类型阴离子的化合物,其晶格能的变化只决定于离 子半径r+的变化。由于镧系元素的Ln2+ 、Ln3+离子半径随原子序 数的变化是平滑的,因而晶格能的变化也应是平滑的,所以上述 △rHm θ 的变化将取决于相应的I3的变化。根据电离能数值 可以得到镧系元素二价离子Ln2+对于氧化反应的稳定性次序为 La<Ce<Pr<Nd<Pm<Sm<Eu>>Gd< Tb<Dy>Ho>Er<Tm<Yb>Lu 其中最稳定的是Eu2+和Yb2+离子。 Eu Yb

2镧系元素+4氧化态的稳定性 镧系元素+4氧化态稳定性可以用前面+2氧化态稳定性的讨 论方法进行类似的讨论。 LnX(s) △Hm6 -→LnX3(s)+1/2X2(参考态) L3 △Hm(X,g Ln+(g)千4X-(g)4Ln3+(g)千3X-(g)+X-(g) 由此有△Hm9=L4一L3一L4一△Hm(X-,g) △Gm≈△Hm9=-L4十L4-L3+常数 式中I4为镧系元素的第四电离能,L3、L4分别是LX,(S)、 LnX4(S的晶格能。△Gm的变化将由L4所决定,I4值越大,上述 反应的自发趋势就越大,意味着LX4越不稳定
2 镧系元素+4氧化态的稳定性 镧系元素+4氧化态稳定性可以用前面+2氧化态稳定性的讨 论方法进行类似的讨论。 △rGm θ≈△rHm θ=-I4+L4-L3+常数 式中I4为镧系元素的第四电离能,L3、L4分别是LnX3 (s)、 LnX4 (s)的晶格能。△rGm θ的变化将由I4所决定,I4值越大,上述 反应的自发趋势就越大,意味着LnX4越不稳定。 LnX4 (s) —————→ LnX3 (s ) + 1/2 X2 (参考态) Ln4+(g)+4X-(g)——→Ln3+(g)+3X-(g)+X-(g) L4 L3 △fHm θ (X-,g) -I4 △rHm θ 由此有 △rHm θ=L4-L3-I4-△fHm θ (X-,g)
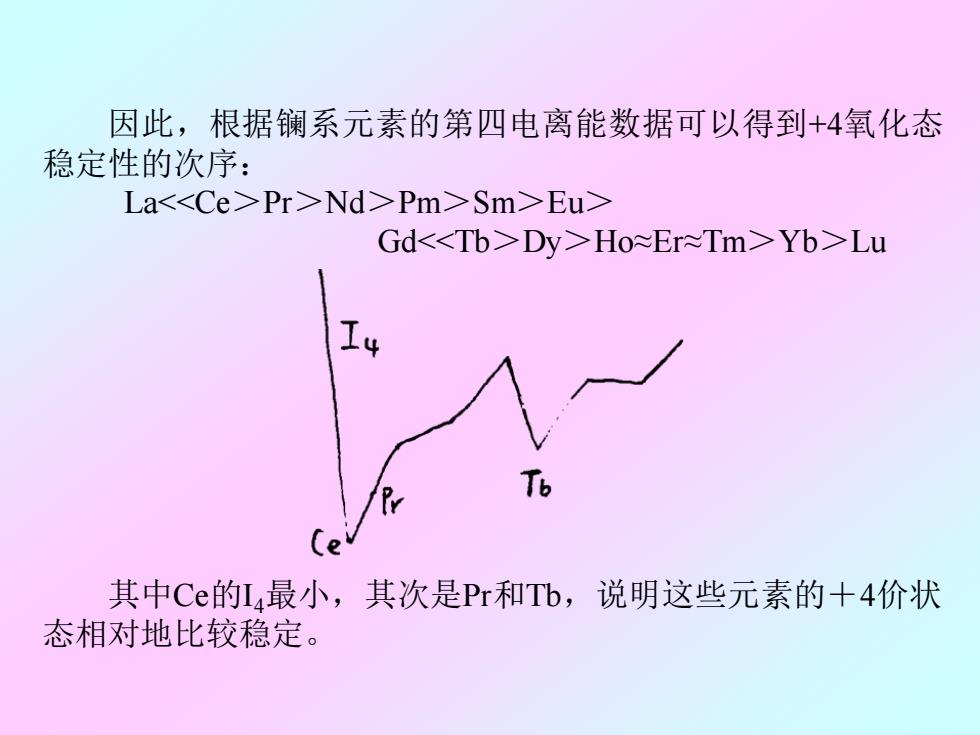
因此,根据镧系元素的第四电离能数据可以得到+4氧化态 稳定性的次序: LaPr>Nd>Pm>Sm>Eu> GdDy>Ho≈Er≈Tm>Yb>Lu Tb 其中Ce的14最小,其次是Pr和Tb,说明这些元素的+4价状 态相对地比较稳定
因此,根据镧系元素的第四电离能数据可以得到+4氧化态 稳定性的次序: La<<Ce>Pr>Nd>Pm>Sm>Eu> Gd<<Tb>Dy>Ho≈Er≈Tm>Yb>Lu 其中Ce的I4最小,其次是Pr和Tb,说明这些元素的+4价状 态相对地比较稳定