
第五章S区元素 基本要求 1复习自由能、平衡常数的概念 2辨别热力学稳定性和动力学稳定性 3能计算离子键形成时的能量变化 4能正确使用理论模型和热力学循环方法计算晶格能 5熟悉晶格能在无机化学中的应用 6能正确建立玻恩一哈伯热化学循环并用以计算各种 热力学量 7冠醚的命名和结构特征 8冠醚的配位性能和冠醚配合物的结构 9影响冠醚配合物稳定性的因素 习题:2,5,6,7,9
基 本 要 求 1 复习自由能、平衡常数的概念 2 辨别热力学稳定性和动力学稳定性 3 能计算离子键形成时的能量变化 4 能正确使用理论模型和热力学循环方法计算晶格能 5 熟悉晶格能在无机化学中的应用 6 能正确建立玻恩-哈伯热化学循环并用以计算各种 热力学量 7 冠醚的命名和结构特征 8 冠醚的配位性能和冠醚配合物的结构 9 影响冠醚配合物稳定性的因素 习题 :2, 5, 6, 7, 9 第五章 s 区 元 素

5.1自由能、化学平衡(复习)和稳定性概念 对反应A(g)十B(g))→C(g)十D(g) △G=△Ge+RTInQ =一RTInKe+RTInQ =RTIn(Q/Ke) pc/pe.Po/po pc/pe.Po/pe KO=K= Q- pe/p.Pp pepPp K为平衡常数,Q为反应商。在K表达式中,PAPB PC、PD是在平衡时刻物种A、B、C、D的分压力。在Q 表达式中的pA、PgPc、PD是任意时刻物种A、B、C、D 的分压力
5.1 自由能、化学平衡(复习)和稳定性概念 △G=△G+RTlnQ =-RTlnK+RTlnQ =RTln(Q/K) K为平衡常数,Q为反应商。在K表达式中,pA、pB、 pC、pD 是在平衡时刻物种A、B、C、D的分压力。在Q 表达式中的pA、pB、pC、pD是任意时刻物种A、B、C、D 的分压力。 对反应 A(g)+B(g) C(g)+D(g) p c p p p p p p p D B A . . = Q= . . B A D p p p p p p p c p K = K

Q是该体系偏离平衡状态的一个衡量尺度。 在已知平衡常数K的情况下,我们可以把这种偏 离定量化,并由此预测该化学体系在达到化学平衡时 向产物方向还是向反应物方向进行的自发性。 Q>K, 根据△G=RTInQ/K,△G>0, 反应向生成反应物方向进行; Q<K,△G<0,反应向生成产物的方向自发进行; Q=K,△G=0,体系处于平衡
在已知平衡常数K的情况下,我们可以把这种偏 离定量化,并由此预测该化学体系在达到化学平衡时 向产物方向还是向反应物方向进行的自发性。 Q<K,△G<0,反应向生成产物的方向自发进行; Q = K, △G = 0, 体系处于平衡。 Q>K, 根据△G=RTlnQ/K, △G>0, 反应向生成反应物方向进行; Q是该体系偏离平衡状态的一个衡量尺度

为了进行参比,对化学有用的另一特定条件是反应物 和产物都处于标准态,此时Q=1,在这种情况下, △G=△G=-RTInK △G的符号和数值的大小反映标准态体系对平衡 态偏离的方向和程度
为了进行参比,对化学有用的另一特定条件是反应物 和产物都处于标准态,此时Q=1,在这种情况下, △G=△G=-RTlnK △G的符号和数值的大小反映标准态体系对平衡 态偏离的方向和程度

另一个十分重要的热力学方程式是: △G=△H-T△S=△U+△(pV)-T△S 其中△$是产物和反应物相对混乱度的一种衡量尺度。显然, 如果气相反应增加了气体的分子数,凝聚相反应分子数增大等, 此时△S>0,将有利于反应。 对有气体参与的反应 △(pV)=△(nRT) 因此,如果对于每生成或消耗1mo的气体,比项贡献在298 K时将小于2.5 kJ-mol-1(8.314×298×10-3<2.,由此,在数 值上实验化学家常将△H和△U等同对待
因此, 如果对于每生成或消耗 1 mol的气体, 此项贡献在298 K时将小于2.5 kJmol-1 (8.314×298×10-3<2.5),由此,在数 值上实验化学家常将△H和△U 等同对待。 另一个十分重要的热力学方程式是: △G=△H-T△S=△U+△(pV)-T△S 其中△S是产物和反应物相对混乱度的一种衡量尺度。显然, 如果气相反应增加了气体的分子数,凝聚相反应分子数增大等, 此时△S>0,将有利于反应。 对有气体参与的反应 △(pV)=△(nRT)
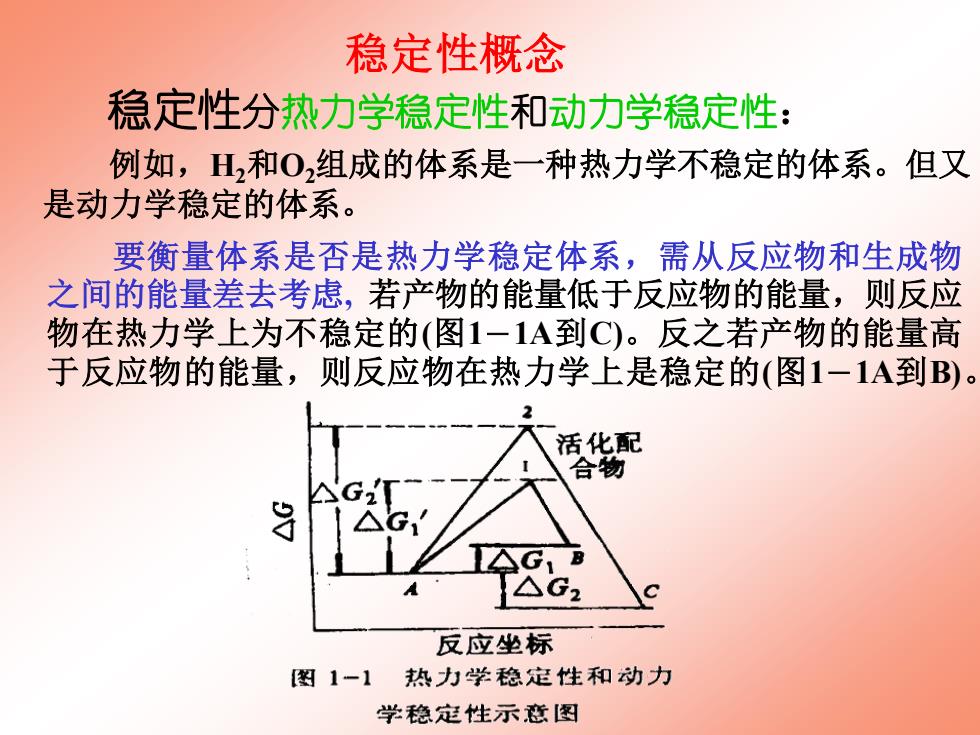
稳定性概念 稳定性分热力学稳定性和动力学稳定性: 例如,H,和0,组成的体系是一种热力学不稳定的体系。但又 是动力学稳定的体系。 要衡量体系是否是热力学稳定体系,需从反应物和生成物 之间的能量差去考虑,若产物的能量低于反应物的能量,则反应 物在热力学上为不稳定的(图1一1A到C)。反之若产物的能量高 于反应物的能量,则反应物在热力学上是稳定的(图1一1A到B)。 活化配 合物 J1 B △G2 反应坐标 图1-1热力学稳定性和动力 学稳定性示意图
稳定性分热力学稳定性和动力学稳定性: 例如,H2和O2组成的体系是一种热力学不稳定的体系。但又 是动力学稳定的体系。 稳定性概念 要衡量体系是否是热力学稳定体系,需从反应物和生成物 之间的能量差去考虑, 若产物的能量低于反应物的能量,则反应 物在热力学上为不稳定的(图1-1A到C)。反之若产物的能量高 于反应物的能量,则反应物在热力学上是稳定的(图1-1A到B)

动力学稳定性是从反应物与活化配合物之间的能量差,即反 应活化能来考虑的,若某一反应物转变为产物的趋势很大,反应 物在热力学上相当不稳定,但若实现这一反应所需的活化能也相 当大的话,则在动力学上反应物又是相当稳定的了(图1一2A到C)。 活化配 合物 AG2还G 反应坐标 图1一2由动力学控制的热 力学不稳定体系 热力学稳定性和动力学稳定性之间没有必然的联系。 催化剂可以改变反应的历程,亦即能改变反应的活化能,因此,催化 剂可以增加或降低动力学稳定性,但催化剂不能改变热力学的稳定性或 不稳定性
热力学稳定性和动力学稳定性之间没有必然的联系。 催化剂可以改变反应的历程,亦即能改变反应的活化能,因此,催化 剂可以增加或降低动力学稳定性,但催化剂不能改变热力学的稳定性或 不稳定性。 动力学稳定性是从反应物与活化配合物之间的能量差,即反 应活化能来考虑的,若某一反应物转变为产物的趋势很大,反应 物在热力学上相当不稳定,但若实现这一反应所需的活化能也相 当大的话, 则在动力学上反应物又是相当稳定的了(图1-2A到C)

5.2离子键形成中的能量 5.2.1 气相离子键形成中的能量 对于反应 Na(g)十Cl(g)一Na+(g)+CI-(g)的能量, Ea 由于反应前后熵改变甚微,△G≈△H,所以, △G≈△H≈lNa)+Ea(C) =495.7+(-348.65) =147.05 kJ-mol-1 说明上述反应的趋势很小
5.2 离子键形成中的能量 5.2.1 气相离子键形成中的能量 由于反应前后熵改变甚微,△G≈△H ,所以, △G≈△H ≈I(Na)+Ea(Cl) =495.7+(-348.65) =147.05 kJmol-1 说明上述反应的趋势很小。 对于反应 Na(g)+Cl(g) Na+(g)+Cl-(g) 的能量, Ea I

带相反电荷的两个离子,可因静电吸引而结合在一起,该 引力为: U2=-9+9 另一方面,两个离子趋近时,因电子层的穿插而导致强排斥力: U3=be-r/p 所以由Na(g)和CI(g)形成Na+CI一(g)离子对时,总能量为: 8=147.05+U2+Ug=147.05-949+ber/p
带相反电荷的两个离子,可因静电吸引而结合在一起,该 引力为: U2=- r q q+ − 另一方面,两个离子趋近时,因电子层的穿插而导致强排斥力: U3=be-r/ρ 所以由Na(g)和Cl(g)形成Na+Cl-(g)离子对时,总能量为: ε=147.05+U2+U3=147.05- +be-r / ρ r q q+ −
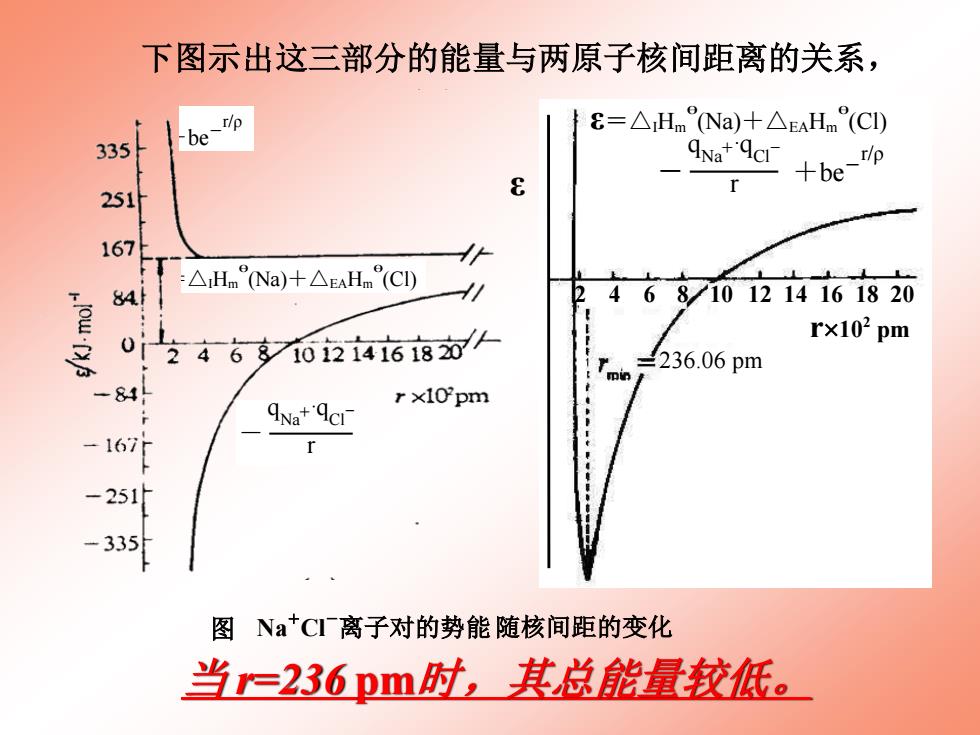
下图示出这三部分的能量与两原子核间距离的关系, be- E=△HmNa)十△EaHm(CI) 335 ANa+'qcI- r +be-p 251 e 167 :△Hm°Na)+△EAHm(CI) 84 24687101214161820 r×102pm 24 6多o2i468茹仆 236.06pm -84 r x1Opm ANat'Acr 16 -251 -335 图Na+CI离子对的势能随核间距的变化 当=236pm时,其总能量校低
当 r=236 pm时,其总能量较低。 下图示出这三部分的能量与两原子核间距离的关系, ε 236.06 pm 2 4 6 8 10 12 14 16 18 20 r102 pm ε=△IHm θ (Na)+△EAHm θ (Cl) - +be- r/ρ q Na +·qCl- r 图 5.8 Na+ Cl- 离子对的势能 随核间距的变化 ε 236.06 pm 2 4 6 8 10 12 14 16 18 20 r102 pm ε=△IHm θ (Na)+△EAHm θ (Cl) - +be- r/ρ q Na +·qCl- r 图 5.8 Na+ Cl- 离子对的势能 随核间距的变化 ε 236.06 pm 2 4 6 8 10 12 14 16 18 20 r102 pm ε=△IHm θ (Na)+△EAHm θ (Cl) - +be- r/ρ q Na +·qCl- r 图 5.8 Na+ Cl- 离子对的势能 随核间距的变化 ε 236.06 pm 2 4 6 8 10 12 14 16 18 20 r102 pm ε=△IHm θ (Na)+△EAHm θ (Cl) - +be- r/ρ q Na +·qCl- r 图 5.8 Na+ Cl- 离子对的势能 随核间距的变化 ε 236.06 pm 2 4 6 8 10 12 14 16 18 20 r102 pm ε=△IHm θ (Na)+△EAHm θ (Cl) - +be- r/ρ q Na +·q Cl - r 图 5.8 Na + Cl - 离子对的势能 随核间距的变化 ε 236.06 pm 2 4 6 8 10 12 14 16 18 20 r102 pm ε=△IHm θ (Na)+△EAHm θ (Cl) - +be- r/ρ q Na +·qCl- r 图 5.8 Na+ Cl- 离子对的势能 随核间距的变化 ε 236.06 pm 2 4 6 8 10 12 14 16 18 20 r102 pm ε=△IHm θ (Na)+△EAHm θ (Cl) - +be- r/ρ q Na +·qCl- r 图 5.8 Na + Cl- 离子对的势能 随核间距的变化