西北大学：《中级无机化学》课程教学课件（专题讲稿）11 平衡态和标准态（PPT）

平衡态和标准态 平衡态是指一个过程或反应所处的一个相对静止的状态。 这时，正反应、逆反应的速率相等，体系中各物种的压力或浓 度处于一个定值，产物的相对浓度或相对压力以其分数作为方 次的乘积与反应物的相对浓度或相对压力以其分数作为方次的 乘积之比是一个常数： aA+bB±cC+dD K=-(c(C)/c)(c(D)/cd (c(A)/c0)a(c(B)/c)b 设Q为反应商，此时（平衡时），K=Q, △G=-RTInK+RTInQ RTInQ/K =0=0

平衡态和标准态 平衡态是指一个过程或反应所处的一个相对静止的状态。 这时，正反应、逆反应的速率相等，体系中各物种的压力或浓 度处于一个定值，产物的相对浓度或相对压力以其分数作为方 次的乘积与反应物的相对浓度或相对压力以其分数作为方次的 乘积之比是一个常数： aA＋bB cC＋dD K＝ 设Q为反应商，此时(平衡时) ，K＝Q， △G＝－RTlnK＋RTlnQ ＝ RTlnQ/K ＝0＝0。 (c(C)／c θ ) c (c(D)／c θ ) d (c(A)／c θ ) a (c(B)／c θ ) b

标准态热力学对标准态有一个严格的定义： 对于纯净的液体和固体，是指一个标准态压力下该液体和固 体本身； 对于气体是指其压力或分压力为一个标准态压力： 对于溶液中的溶质，溶质的浓度为1ol·L-1的理想溶液。 这样一来，在标准态时，物质的浓度和压力只有一个值（不可 能有其它值)，此时（标准态时）， Q=1 △G=△G9+RTInQ=△G9=-RTInK 这时，△G的值和符号是处于该状态（标准态）这种特定情况 时，体系离平衡有多远的量度。 这里需要说明的是：标准态时，Q=1;但Q=1时却不一定是 标准态。 还有多种状态时Q也可能为1：在Q的表达式中，分子、分母 的值相等（不管具体值是多少，只要相等就行了）。当然这些状态不 一定是标准态

标准态热力学对标准态有一个严格的定义： 对于纯净的液体和固体，是指一个标准态压力下该液体和固 体本身； 对于气体是指其压力或分压力为一个标准态压力； 对于溶液中的溶质，溶质的浓度为1mol·L－1的理想溶液。 这样一来，在标准态时，物质的浓度和压力只有一个值(不可 能有其它值)，此时(标准态时)， Q＝1 △G＝△Gθ＋RTlnQ＝△Gθ＝－RTlnK 这时，△Gθ的值和符号是处于该状态(标准态)这种特定情况 时，体系离平衡有多远的量度。 这里需要说明的是：标准态时，Q＝1；但Q＝1时却不一定是 标准态。 还有多种状态时Q也可能为1：在Q的表达式中，分子、分母 的值相等(不管具体值是多少，只要相等就行了)。当然这些状态不 一定是标准态

所以，平衡态时， K=Q,△G=-RTInK+RTInQ RTInQ/K 三0 K不一定等于1（当然也可能为1）。△G不一定等于0（当然 也可能为0)。 标准态时， Q=1,△G=-RTInK+RTlnQ RTIn(1/K) =-RTInK=△G9 K不一定等于1（当然也可能为1）。△G不一定等于0（当然 也可能为0)

所以，平衡态时， K＝Q，△G＝－RTlnK＋RTlnQ ＝ RTlnQ/K ＝0 K不一定等于1(当然也可能为1)。 △Gθ不一定等于0(当然 也可能为0) 。 标准态时， Q＝1，△G＝－RTlnK＋RTlnQ ＝ RTln(1/K) ＝－RTlnK＝△Gθ K不一定等于1 (当然也可能为1)。△Gθ不一定等于0(当然 也可能为0)

热力学规定了纯物质的标准态，过去，纯物质的有关热力学 数据都是以1atm”作为标准态压力公布的。席卷世界的推行国 际制单位的运动已使“atm”成为一种过时的压力单位，在一些国 家中，使用“atm”已成为非法，我国已于1985年9月正式颁布并 于1986年7月1日起开始实施计量法。计量法明确规定废止“atm 压力单位，而代之以“帕斯卡(Pa)”。为此，传统的热力学标准态 压力“1atm有待于从国际制单位的角度加以重新审定。 就热力学范畴而言，当然可以用以SI单位表示的latm的 101.325kPa作为标准态压力，或改用其它压力作为标准态压力。 考虑到： 1.新的标准态压力应当与低海拔地表的实际平均大气压接近； 2.新的标准态在所选定的单位表示时数值上应等于1（如同旧标 准态压力latm); 3.新建立的标准态压力应该使原有的热力学数据表的变动最小： 4. 用新的标准态压力进行平衡常数和l(ppo)计算时应和用I旧的 latm同样方便； 5.新的标准态压力应与SI单位协调一致

热力学规定了纯物质的标准态，过去，纯物质的有关热力学 数据都是以1“atm”作为标准态压力公布的。席卷世界的推行国 际制单位的运动已使“atm”成为一种过时的压力单位，在一些国 家中，使用“atm”已成为非法，我国已于1985年9月正式颁布并 于1986年7月1日起开始实施计量法。计量法明确规定废止“atm” 压力单位，而代之以“帕斯卡(Pa)”。为此，传统的热力学标准态 压力“1atm”有待于从国际制单位的角度加以重新审定。 就热力学范畴而言，当然可以用以SI单位表示的1atm的 101.325 kPa作为标准态压力，或改用其它压力作为标准态压力。 考虑到： 1. 新的标准态压力应当与低海拔地表的实际平均大气压接近； 2. 新的标准态在所选定的单位表示时数值上应等于1(如同旧标 准态压力1atm)； 3. 新建立的标准态压力应该使原有的热力学数据表的变动最小； 4. 用新的标准态压力进行平衡常数和ln(p/p0 )计算时应和用旧的 1atm同样方便； 5. 新的标准态压力应与SI单位协调一致

于是，在众多的可供选择的新标准态压力（包括101.325kPa) 中，国际理论与应用化学联合会(IUPAC)于1982年决定以1bar(= 105Pa=0.986923atm=750.064mmHg)作为新的标准态压力(SSP, Standard State Pressure)。以bar作为新的SSP是其下属机构一热力 学委员会于1981年倡议的，IUPAC在1982年正式批准并公布。按 照这一新的S$P的热力学数据表已经问世，一些教科书也作了相 应的变更，如北京大学华彤文教授的《普通化学原理》 。 标准态压力的这一新的变动对纯物质的热力学数据将产生不 同的影响。 压力从1atm变为1bar基本上不改变纯物质的标准 生成焓数据，即△H=△H(角号“表示建立在新的SSP基 础上的热力学数据，角号“a”则代表在latm下的数据)。因为压 力由latm(1.01325bar)变为1bar,其改变甚微，故对固体与液体 的焓值都无明显影响，对于气体，标准态条件意味着理想气体行 为，而理想气体的焓与压力无关

于是，在众多的可供选择的新标准态压力(包括101.325 kPa) 中，国际理论与应用化学联合会(IUPAC)于1982年决定以1bar(＝ 105 Pa＝0.986923 atm＝750.064 mmHg)作为新的标准态压力(SSP， Standard State Pressure)。以bar作为新的SSP是其下属机构—热力 学委员会于1981年倡议的，IUPAC在1982年正式批准并公布。按 照这一新的SSP的热力学数据表已经问世，一些教科书也作了相 应的变更，如北京大学华彤文教授的《普通化学原理》。 标准态压力的这一新的变动对纯物质的热力学数据将产生不 同的影响。 压力从1 atm变为1 bar基本上不改变纯物质的标准 生成焓数据，即ΔHθ＝ΔHa (角号“θ”表示建立在新的SSP基 础上的热力学数据，角号“a”则代表在1atm下的数据)。因为压 力由1atm (1.01325 bar)变为1 bar，其改变甚微，故对固体与液体 的焓值都无明显影响，对于气体，标准态条件意味着理想气体行 为，而理想气体的焓与压力无关

对于熵值，SSP的这一变动同样不会造成固体和液体 熵值的明显变化，因为压力的变化所造成的熵值的变化远小于 固体和液体的熵值的实验误差。然而，尽管S$P的上述变化使 气体的摩尔熵值明显低于由量热法数据所得到的熵的实 验误差，但这种改变有可能不低于由光谱法所得到的实 验误差或由统计热力学所得到的值，所以应加以校正： S9=a+δ 此处，6为改变量，δ=R1n1.01325=0.10944JK-1mol-1。 气体标准摩尔熵值的改变势必会引起纯物质标准生 成自由焓和化学反应的标准自由焓变的变化。 例如，对于生成反应，可以导出 △Gm9=△rGma-δT2v(g) 式中，ω(g)为反应中各气体组份化学计量系数之代数和，对于反 应物，系数符号为负，生成物系数符号为正。 对于标准电极电势：E=Ea-δTω(g)/nF

对于熵值，SSP的这一变动同样不会造成固体和液体 熵值的明显变化，因为压力的变化所造成的熵值的变化远小于 固体和液体的熵值的实验误差。然而，尽管SSP的上述变化使 气体的摩尔熵值明显低于由量热法数据所得到的熵的实 验误差，但这种改变有可能不低于由光谱法所得到的实 验误差或由统计热力学所得到的值，所以应加以校正： S θ＝S a＋δ 此处，δ为改变量，δ＝Rln1.01325＝0.10944 J·K－1·mol－1 。 气体标准摩尔熵值的改变势必会引起纯物质标准生 成自由焓和化学反应的标准自由焓变的变化。 例如，对于生成反应，可以导出 △fGm θ＝△fGm a－δTΣυ(g) 式中，Συ(g)为反应中各气体组份化学计量系数之代数和，对于反 应物，系数符号为负，生成物系数符号为正。 对于标准电极电势：E θ＝E a－δTΣυ(g)／nF

如果要将平衡常数表达式Ka中的压力由atm改为bar,那么， 得加上一校正系数 K9=K(1.01325)(g) 下表给出了在298.15K,压力从1atm变为1bar是纯物质的 些热力学函数的变化值。对于大多数物质来说，这种变化值均明 显低于热力学的数据误差。因此，即使你粗心地将“新SSP”数据 与“I旧SSP数据完全混淆，也不致犯重大的错误。 热力学数 摩尔体积 △H-△Ha △G9-△Ga o-Cp Se-Sa 物质 据 cm3/mol J/mol J/mol J/K.mol J/K:mol 理想气体 24.7894 0 -32.630 0 0.1094 H,0 18 -0.022 -0.024 7×10-5 5.0×10 6 C6H12①) 115 -0.080 -0.152 2×10-4 2.4×10 4 *豳气体的摩体积在传统气体定律3P(标推诅瘦和4压力0 27315K和1atm)下为22.4138dm3mdl,若在1br和2731K卞为 22.7108dm/mol,若在热力学常用的参考温度298.15K和1bar下为 24.7894≈24.8dm3mol

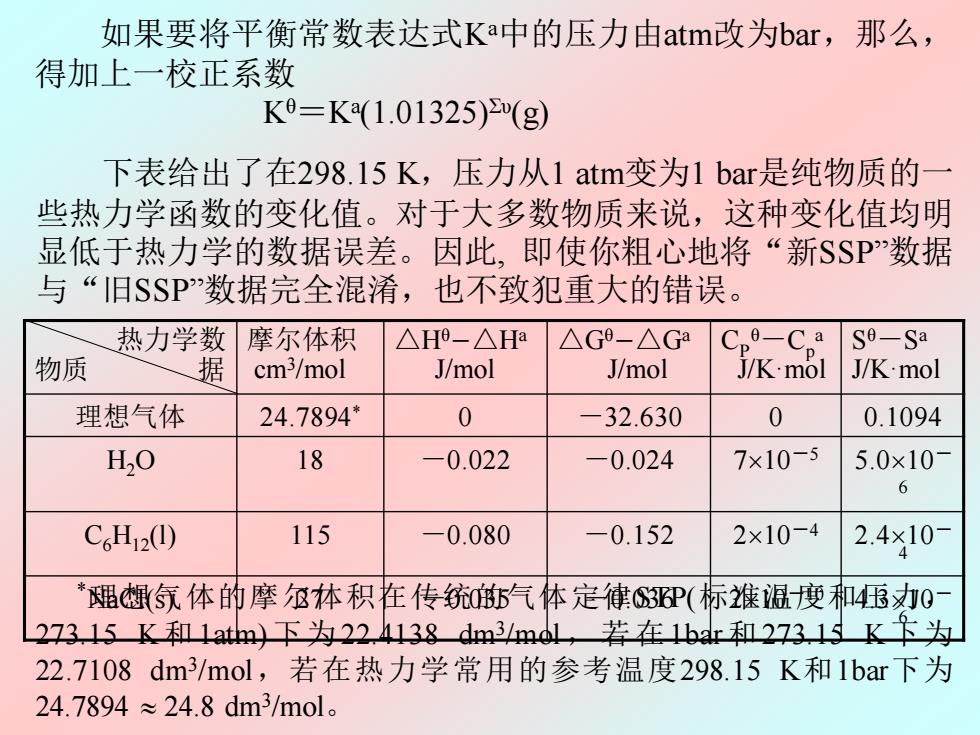
如果要将平衡常数表达式Ka中的压力由atm改为bar，那么， 得加上一校正系数 Kθ＝Ka (1.01325) Συ(g) 热力学数 物质 据 摩尔体积 cm3 /mol △Hθ－△Ha J/mol △Gθ－△Ga J/mol CP θ－Cp a J/K·mol S θ－S a J/K·mol 理想气体 24.7894* 0 －32.630 0 0.1094 H2O 18 －0.022 －0.024 710－5 5.010－ 6 C6H12(l) 115 －0.080 －0.152 210－4 2.410－ 4 NaCl(s) 27 －0.035 －0.036 210－10 4.310－ 6 *理想气体的摩尔体积在传统的气体定律STP(标准温度和压力， 273.15 K和 1atm) 下为 22.4138 dm3 /mol ， 若 在1bar和 273.15 K下为 22.7108 dm3 /mol，若在热力学常用的参考温度298.15 K和1bar下为 24.7894  24.8 dm3 /mol。 下表给出了在298.15 K，压力从1 atm变为1 bar是纯物质的一 些热力学函数的变化值。对于大多数物质来说，这种变化值均明 显低于热力学的数据误差。因此, 即使你粗心地将“新SSP”数据 与“旧SSP”数据完全混淆，也不致犯重大的错误

然而，IUPAC批准的倡议对应用在其他方面的标准压力(SP) 还没有约束力。例如，S$P的改变对物质的凝固点和熔点不会产 生明显的影响，但是，如果由1atm变到1bar,物质的沸腾和升 华的温度将有不同的改变（如，在1bar的SSP下水的沸点将是 99.975℃而不是100.00C),然而，这些常用的各种“正常 点”（如熔点、沸点、升华点等）的压力是101.325kPa,不在规定 之列。但是，已经有人建议使用大气压沸点(abp,atmospheric boiling point)和巴沸点(bbp,baric boiling point)这两个名称来代替 原来的“正常沸点”(normal boiling point)。以避免在SSP的改变 后读者对沸点（升华点）所参照的压力所发生的混淆。同样，也建 议用标准环境温度与压力(SATP,Standard ambient temperature and pressure,298.15K-IUPAC:推荐的热力学常用参考温度和Ibar) 代替气体定律传统采用的STP(标准温度和压力，273.15K和1ba)。 显然，SSP这一重要变革将对科学和技术界，对各种水平的 化学教育产生重要的影响，若对本问题感兴趣并希望更深入了解 的请参阅参考文献一4

然而，IUPAC批准的倡议对应用在其他方面的标准压力(SP) 还没有约束力。例如，SSP的改变对物质的凝固点和熔点不会产 生明显的影响，但是，如果由1 atm变到1 bar，物质的沸腾和升 华的温度将有不同的改变(如，在1bar的SSP下水的沸点将是 99.975oC 而不是 100.00oC) ，然 而 ， 这 些常 用 的 各 种“ 正 常 点”(如熔点、沸点、升华点等)的压力是101.325 kPa，不在规定 之列。但是，已经有人建议使用大气压沸点(abp，atmospheric boiling point)和巴沸点(bbp，baric boiling point)这两个名称来代替 原来的“正常沸点”(normal boiling point)。以避免在SSP的改变 后读者对沸点(升华点)所参照的压力所发生的混淆。同样，也建 议用标准环境温度与压力(SATP，Standard ambient temperature and pressure, 298.15 K－IUPAC推荐的热力学常用参考温度和1bar) 代替气体定律传统采用的STP(标准温度和压力，273.15K和1bar)。 显然，SSP这一重要变革将对科学和技术界，对各种水平的 化学教育产生重要的影响，若对本问题感兴趣并希望更深入了解 的请参阅参考文献[1－4]

[1]IUPAC,"Appendix IV",Manual of Symbols and Terminology for Physicochemical Quantities an units,Pure And Appl.Chem.,1982 54,1239,J.Chem.Thermodyn.,1982,14,805. [2]R.D.Freeman,High,Temp,Sci.,1979,11,73. [3]R.D.Freeman,J.Chem.Educ.,1985,62,681 [4]R.D.Freeman,"International Newstet Tercon Chemical Education'”,24,No.21,June(1984);方锡义译，大学化学， 1986,2,13,31-32

[1] IUPAC, “Appendix Ⅳ”, Manual of Symbols and Terminology for Physicochemical Quantities an units,Pure And Appl. Chem., 1982, 54, 1239; J. Chem. Thermodyn.,1982, 14, 805. [2] R. D. Freeman, High, Temp, Sci., 1979, 11, 73. [3] R. D. Freeman, J. Chem. Educ., 1985, 62, 681. [4] R. D. Freeman, “International Newstet Tercon Chemical Education”, 2～4, No. 21, June (1984); 方锡义译，大学化学， 1986, 2, 13, 31-32