
对第一过渡系元素的氧化还原性的讨论 1第一过渡系电对MP+M的电极电势 过渡金属电对MP+M的电极电势E(MP+M)可由下列反应的△,Gm求算。 M(s)+2H+(aq)=H2(g)+M2+(aq) 若将该反应设计成一个原电池,并忽略过程的嫡变,则 △,Gm≈△H(电池)≈-2FE(电池)=2Fφ(MP+M0 对该反应,可以设计一个玻恩-哈伯热化学循环: 2△Hm(D) 2H+(g → 2H(g) -2△waHm(Ht,g 于△bHm9(H2,g) M(s)+2H(aq) H(电池) 2(g)+M2+(aq) △atmHm9(M,s) △tydHm(M2+,g) M(g) M+(g) △1+2HmM,g △Hm(电池)=(△amHm0+△a+2)Hn9+△wdHm)M -2(△dHm9+△Hm+12△,Hma
对第一过渡系元素的氧化还原性的讨论 1 第一过渡系电对M2+/M的电极电势 过渡金属电对M2+/M的电极电势E (M2+/M)可由下列反应的△rGm θ求算。 M(s) + 2H+(aq) = H2 (g) + M2+(aq) 若将该反应设计成一个原电池,并忽略过程的熵变,则 △rGm θ≈△rHm θ (电池)≈-2FE (电池)=2Fφ (M2+/M) 对该反应,可以设计一个玻恩-哈伯热化学循环: △rHm θ (电池)=(△atmHm θ+ △I(1+2) Hm θ+ △hydHm θ )M -2(△hydHm θ+△IHm θ+1/2△bHm θ )H -2△IHm θ (H) 2H+(g) ────→ 2H(g) -2△hydHm θ (H+ , g) -△bHm θ (H2 , g) M(s) + 2H+(aq) ────→ H2 (g) + M2+(aq) △atmHm θ (M, s) △hydHm θ (M2+ , g) M(g) ───────────────→M2+(g) △Hθ (电池) △I(1+2)Hm θ (M,g)
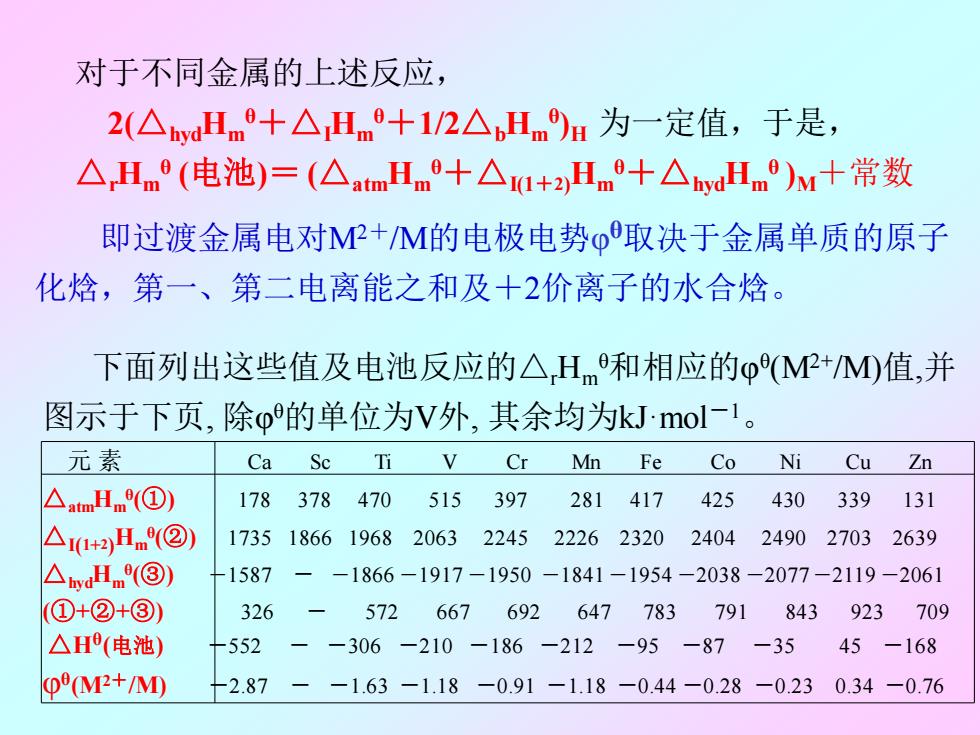
对于不同金属的上述反应, 2(△wdHm+△Hm°+1/2△Hm)u为一定值,于是, △,Hm°(电池)=(△mHm+△+2Hnm+△wdHm)+常数 即过渡金属电对MP+M的电极电势o取决于金属单质的原子 化焓,第一、第二电离能之和及十2价离子的水合焓。 下面列出这些值及电池反应的△Hm和相应的o(MP+M)值,并 图示于下页,除o的单位为V外,其余均为kJmol-1。 元素 Ca Sc Ti V Cr Mn Fe Co Ni Cu Zn △atmHm(①) 178 378470 515397 281417 425 430339 131 △+2Hm②) 17351866196820632245222623202404249027032639 △wdm③) 1587 -1866-1917-1950-1841-1954-2038-2077-2119-2061 (①+②+③) 326 572 667 692 647 783 79 843 923 709 △H(电池) +552 -306-210-186 -212 -95 -87 -35 45 -168 (M2+/M) -2.87 一 -1.63-1.18-0.91-1.18-0.44-0.28-0.230.34-0.76
对于不同金属的上述反应, 2(△hydHm θ+△IHm θ+1/2△bHm θ )H 为一定值,于是, △rHm θ (电池)= (△atmHm θ+△I(1+2)Hm θ+△hydHm θ )M+常数 即过渡金属电对M2+/M的电极电势φ θ取决于金属单质的原子 化焓,第一、第二电离能之和及+2价离子的水合焓。 下面列出这些值及电池反应的△rHm θ和相应的φ θ (M2+ /M)值,并 图示于下页, 除φ θ的单位为V外, 其余均为kJ·mol-1 。 元 素 Ca Sc Ti V Cr Mn Fe Co Ni Cu Zn △atmHm θ (①) 178 378 470 515 397 281 417 425 430 339 131 △I(1+2)Hm θ (②) 1735 1866 1968 2063 2245 2226 2320 2404 2490 2703 2639 △hydHm θ (③) -1587 - -1866 -1917 -1950 -1841 -1954 -2038 -2077 -2119 -2061 (①+②+③) 326 - 572 667 692 647 783 791 843 923 709 △Hθ (电池) -552 - -306 -210 -186 -212 -95 -87 -35 45 -168 φθ (M2+/M) -2.87 - -1.63 -1.18 -0.91 -1.18 -0.44 -0.28 -0.23 0.34 -0.76
(I)△atmHme(曲线④), 25 H8 呈双峰状。金属原子化需 2 要破坏金属键,而金属键的强 20 ⑧ 9 3 度与成单d电子的数目有关, 17 2 4 由Ca的0到Mn的5再到Zn的0, 0 破坏金属键需要消耗的能量应 100 ③ 200 有近似抛物线形式的变化规律 0 +0.5 ;但另一方面,金属原子化使 ②0 具有正常键合的相邻原子的自 -0.5 010% 旋一自旋偶合解体,使自旋平 ② -15 行的电子对数目增多,释放出 -2.0 交换能。根据交换能的概念, -2.5 未成对的电子数越多释放出的 Ca Se Ti V Cr Mn Fe Co Ni Cu Zn 交换能越多,因而这部分能量 图第一过渡系元素的一些热数据的图示 应有近似反抛物线形。将二者 (除p的单位为V外,其余各△H的单位均为kJmol) 加合将得到曲线④
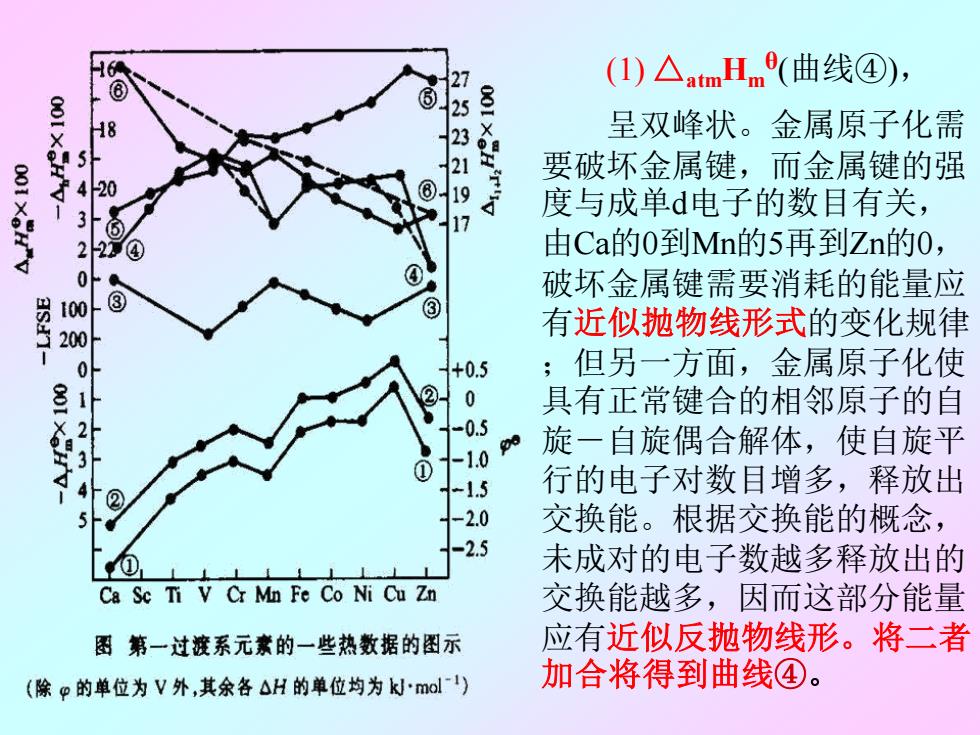
(1) △atmHm θ (曲线④), 呈双峰状。金属原子化需 要破坏金属键,而金属键的强 度与成单d电子的数目有关, 由Ca的0到Mn的5再到Zn的0, 破坏金属键需要消耗的能量应 有近似抛物线形式的变化规律 ;但另一方面,金属原子化使 具有正常键合的相邻原子的自 旋-自旋偶合解体,使自旋平 行的电子对数目增多,释放出 交换能。根据交换能的概念, 未成对的电子数越多释放出的 交换能越多,因而这部分能量 应有近似反抛物线形。将二者 加合将得到曲线④
6 H8 713231 (2)△1+2)Hm(曲线⑤) 5 总的说来是增加的,但在 1X8 4 20 Cr和Cu处出现了凸起。其总趋 2 2 0 势归因于有效核电荷的增加, 100 ③ 200 凸起则是因其余元素都是 0 +0.5 8 @ 3d4s2, 0 2 -0.5 而Cr却为3d54sl、Cu为3d104s1之 34 ① -1.09 -1.5 故。 ② -2.0 -2.5 (3)△bydHm(曲线⑥) Ca Sc Ti V Cr Mn Fe Co Ni Cu Zn 图第一过渡系元素的一些热数据的图示 呈反双峰状。反双峰形变 (除p的单位为V外,其余各△H的单位均为kmal) 化归因于配位场稳定化能(曲线 ③)的贡献
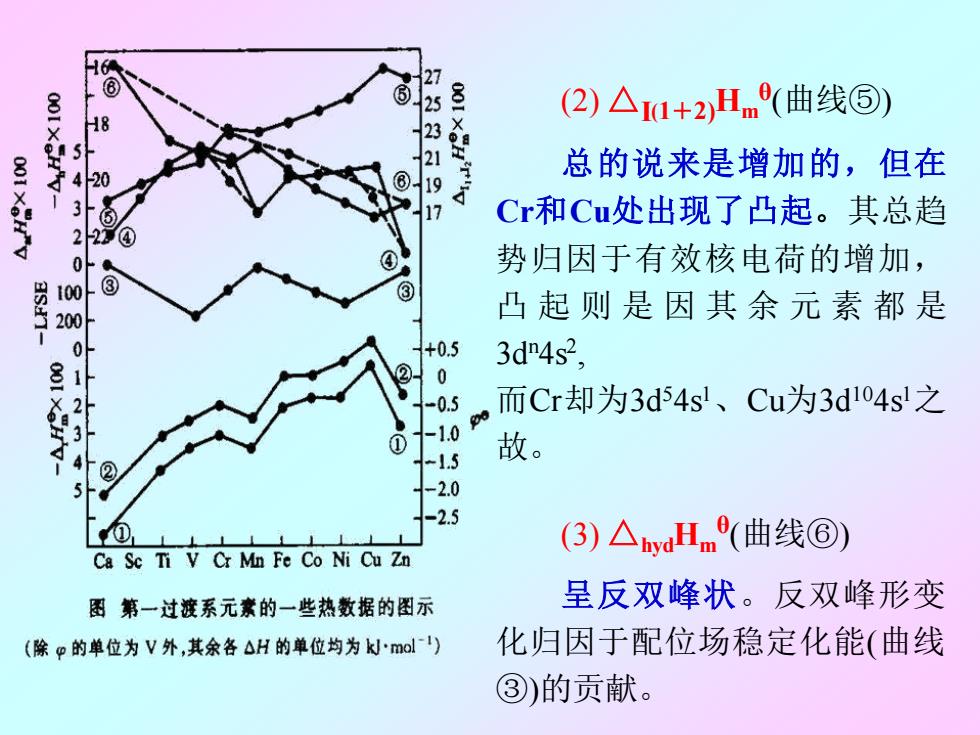
(2) △I(1+2)Hm θ (曲线⑤) 总的说来是增加的,但在 Cr和Cu处出现了凸起。其总趋 势归因于有效核电荷的增加, 凸起则是因其余元素都是 3d n4s 2 , 而Cr却为3d 54s 1 、Cu为3d 104s 1之 故。 (3) △hydHm θ (曲线⑥) 呈反双峰状。反双峰形变 化归因于配位场稳定化能(曲线 ③)的贡献
将这三条曲线加起来,再加上关于氢 25 -18 的各项得到图中表示△H的曲线②。该 001 XSH"V 20 曲线从左到右向上倾斜,很明显,这是由 17 △u+2Hm所控制的。曲线的不规则性归 100 于△mHmo和△H的变化,前者呈双 200 峰状,后者呈反双峰状,只是后者变化的 0 +0.5 0 幅度比前者小(这是因为配位场稳定化能 的贡献不是太大的缘故),二者叠加到一 ① -13 -2.0 块再加到△u+Hm之上就得到△H(曲 -2.5 线②)的变化趋势。可以看到,除个别地 Ca Se Ti V Cr Mn Fe Co Ni Cu Zn 方外,整个△H的变化都与原子化焓的变 图第一过渡系元素的一些热数据的图示 化一致,只是幅度稍小一些而已。 (除p的華位为V外,其余各△H的单位均为灯mdl) 曲线①为p(MP+M)的变化曲线,它与△Hm曲线基本平行。 从这条曲线可以看到,Fe、Co、Ni及Cu的还原性均不如Zn,这 是由于这些元素的成单d电子对强化金属键作出了贡献,Zn没有 成单的d电子,没有这种贡献,所以Zn的还原性强。Mn的还原性 大于Cr,这是由于Mn+的五个未成对d电子的特殊的稳定性和Cr 由3d54s转变为3d4要失去一个d电子需消耗较多的能量之故
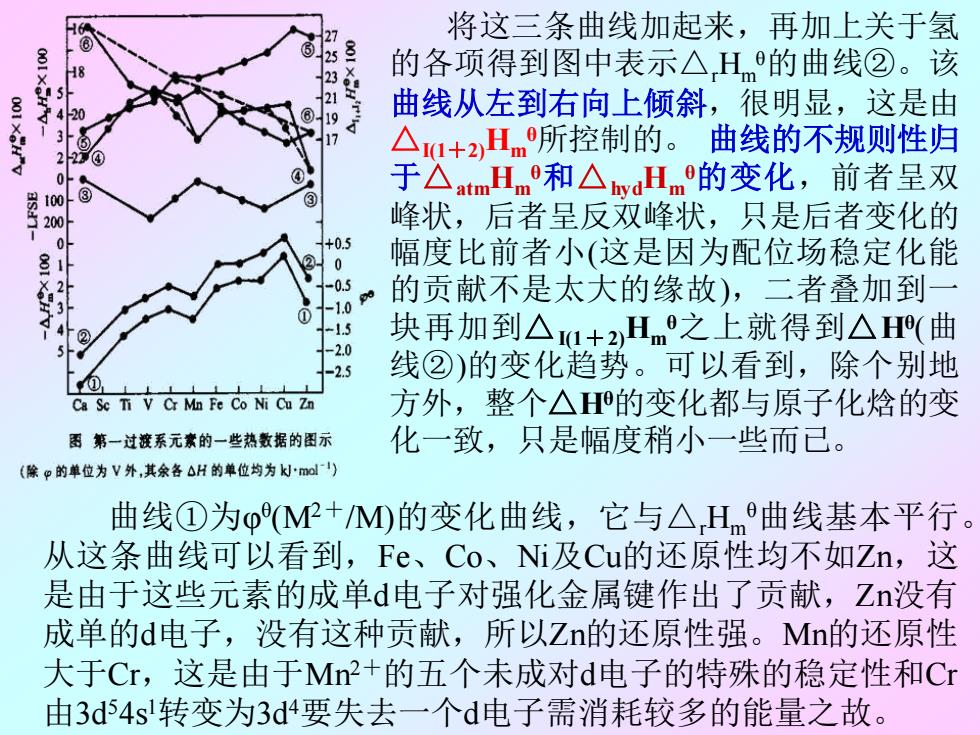
将这三条曲线加起来,再加上关于氢 的各项得到图中表示△rHm θ的曲线②。该 曲线从左到右向上倾斜,很明显,这是由 △I(1+2)Hm θ所控制的。 曲线的不规则性归 于△atmHm θ和△hydHm θ的变化,前者呈双 峰状,后者呈反双峰状,只是后者变化的 幅度比前者小(这是因为配位场稳定化能 的贡献不是太大的缘故),二者叠加到一 块再加到△I(1+2)Hm θ之上就得到△Hθ (曲 线②)的变化趋势。可以看到,除个别地 方外,整个△Hθ的变化都与原子化焓的变 化一致,只是幅度稍小一些而已。 曲线①为φ θ (M2+/M)的变化曲线,它与△rHm θ曲线基本平行。 从这条曲线可以看到,Fe、Co、Ni及Cu的还原性均不如Zn,这 是由于这些元素的成单d电子对强化金属键作出了贡献,Zn没有 成单的d电子,没有这种贡献,所以Zn的还原性强。Mn的还原性 大于Cr,这是由于Mn2+的五个未成对d电子的特殊的稳定性和Cr 由3d 54s 1转变为3d 4要失去一个d电子需消耗较多的能量之故

2第一过渡系电对M3+M2+的电极电势 过渡金属电对MB+MP+的电极电势E(MB+MP+)可由反应的△G求算。 M3+(aq)+1/2H2(g)=H+(aq)+M2+(aq) 由于反应是在溶液中进行的,因而与单质无关,不受原子化焓的影响。 若将该反应设计成一个原电池,并忽略过程的嫡变,则 △G≈△H(电池)≈一FE(电池)=一F0(M+M2+) 对该反应,可以设计一个玻恩一哈伯热化学循环: △Hm(H田 H(g) H+(g) 1/2△bHm(H2,g) △H(电池) △waHm(H+,g M3+(aq)+1/2H2(g) H+(aq)+M2+(aq) -△hdHm(M3+,g △hydHm(MP+,g M+(g) →MP+(g) -△HmM2+, △H(电池)=(1/2△,Hmf+△Hn9+△waHn)H- [△bydHm(M3+)+△BHmA-△Hm(MP+lN
2 第一过渡系电对M3+/M2+的电极电势 过渡金属电对M3+/M2+的电极电势E (M3+/M2+)可由反应的△G求算。 M3+(aq) + 1/2H2 (g) = H+(aq) + M2+(aq) 由于反应是在溶液中进行的,因而与单质无关,不受原子化焓的影响。 若将该反应设计成一个原电池,并忽略过程的熵变,则 △G ≈ △H (电池) ≈ -FE (电池) =-Fφ (M3+/M2+) 对该反应,可以设计一个玻恩-哈伯热化学循环: △Hθ (电池) = (1/2△bHm θ + △IHm θ + △hydHm θ )H - [△hydHm θ (M3+)+ △I3Hm θ-△hydHm θ (M2+)]M △IHm θ (H) H (g) ────→ H +(g) 1/2△bHm θ (H2 , g) △hydHm θ (H+ , g) M3+ (aq) +1/2H2 (g) ────→H+(aq) + M2+(aq) -△hydHm θ (M3+ ,g) △hydHm θ (M2+ , g) M3+(g) ──────────────→M2+(g) △Hθ (电池) -△I3Hm θ (M2+ ,g)

对于不同金属的上述反应, (12△Hm9+△Hm9+△aHnm)H为一定值,于是, △Hm(电池)=-△bydHm(M3+)+△gHm9-△hydHm(M2+川M十常数 即过渡金属电对M3+/MP+的电极电势E与原子的第三电离 能和两种离子的水合焓之差。 由于△3Hn值比△hydHm大得多,历以影响电对电极电赘p°的决 定因素为△3Lm,由下表可看出△3Hm和φ二者之间的关系, 元素 Ca Sc Ti Cr Mn Fe Co Ni Cu △3Hm0 49122386265228282978324829573232339335543833 φM+/MP+ -0.37-0.256-0.41+1.51+0.771+1.81 反常的情况是o(Cr3+/Cr2+)突出地低,这是由于Cr2+的t2g3eg 转变为Cr3+的2g3eg0,伴随着配位场稳定化能的增加,有额外的 能量放出之故,而其他离子,如T2+(2g2)、V2+(23)转变为M3+ 时都有配位场稳定化能的损失之故
对于不同金属的上述反应, (1/2△bHm θ+△IHm θ+△hydHm θ )H为一定值,于是, △rHm θ (电池)=-[△hydHm θ (M3+)+△I3 Hm θ-△hydHm θ (M2+)]M+常数 即过渡金属电对M3+/M2+的电极电势E θ与原子的第三电离 能和两种离子的水合焓之差。 由于△I3Hm θ值比△hydHm θ大得多,所以影响电对电极电势φ θ的决 定因素为△I3Hm θ ,由下表可看出△I3Hm θ和φ θ二者之间的关系, 反常的情况是φ θ (Cr3+/Cr2+)突出地低,这是由于Cr2+的t2g 3eg 1 转变为Cr3+的t2g 3eg 0 ,伴随着配位场稳定化能的增加,有额外的 能量放出之故,而其他离子,如Ti2+(t2g 2 )、V2+(t2g 3 )转变为M3+ 时都有配位场稳定化能的损失之故。 元 素 Ca Sc Ti V Cr Mn Fe Co Ni Cu Zn △I3 Hm θ 4912 2386 2652 2828 2978 3248 2957 3232 3393 3554 3833 φθ (M3+/M2+ ) - - -0.37 -0.256 -0.41 +1.51 +0.771 +1.81 - - -