
过渡系元素的磁性 磁性 磁矩的计算 √纯自旋磁矩 √轨道磁性对磁矩的贡献 √旋一轨偶合对磁性的影响
过渡系元素的磁性 ✓ 磁性 ✓ 磁矩的计算 ✓ 纯自旋磁矩 ✓ 轨道磁性对磁矩的贡献 ✓ 旋-轨偶合对磁性的影响
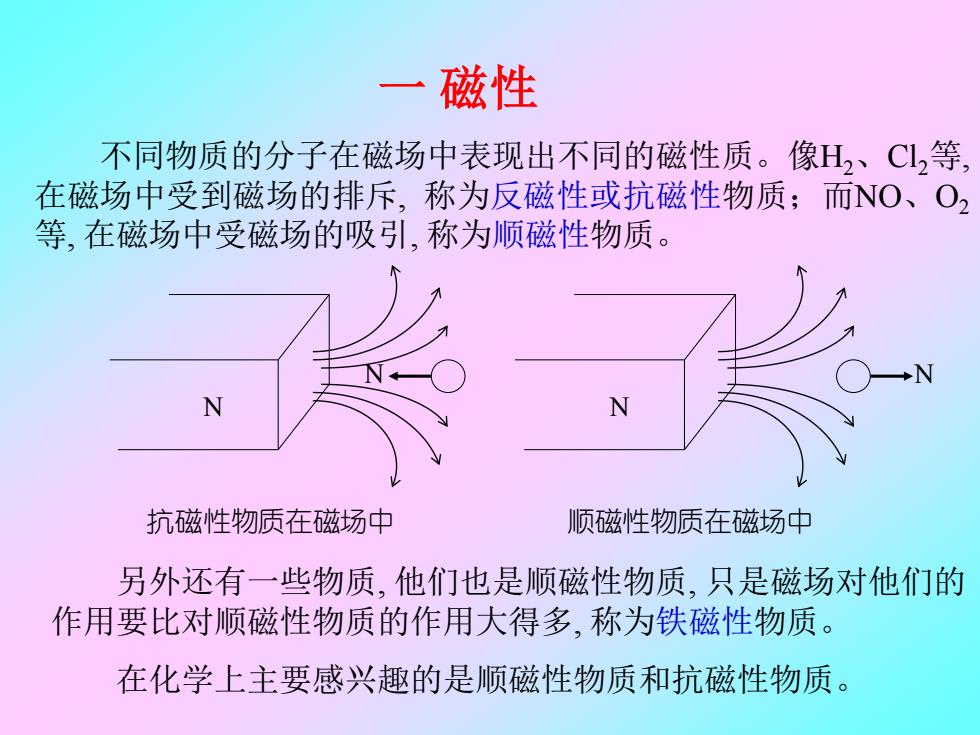
一磁性 不同物质的分子在磁场中表现出不同的磁性质。像H2、C,等, 在磁场中受到磁场的排斥,称为反磁性或抗磁性物质;而O、O2 等,在磁场中受磁场的吸引,称为顺磁性物质。 N N 抗磁性物质在磁场中 顺磁性物质在磁场中 另外还有一些物质,他们也是顺磁性物质,只是磁场对他们的 作用要比对顺磁性物质的作用大得多,称为铁磁性物质。 在化学上主要感兴趣的是顺磁性物质和抗磁性物质
一 磁性 不同物质的分子在磁场中表现出不同的磁性质。像H2、Cl2等, 在磁场中受到磁场的排斥, 称为反磁性或抗磁性物质;而NO、O2 等, 在磁场中受磁场的吸引, 称为顺磁性物质。 N N 抗磁性物质在磁场中 N N 顺磁性物质在磁场中 另外还有一些物质, 他们也是顺磁性物质, 只是磁场对他们的 作用要比对顺磁性物质的作用大得多, 称为铁磁性物质。 在化学上主要感兴趣的是顺磁性物质和抗磁性物质

分子中的电子在绕核的轨道运动和电子本身的自旋运动都 会产生磁效应。电子自旋运动产生自旋角动量,从而产生自旋 磁矩;电子的轨道运动产生的轨道角动量,产生轨道磁矩。当 把分子作为一个整体看时,构成分子的各个电子对外界产生的 磁效应的总和可用一个等效的环电流(称为分子电流)表示,这 个环电流具有一定的磁矩,称为分子磁矩。在多数情况下,分 子磁矩主要是由电子自旋产生的。如果物质的原子或分子轨道 中,所有的电子都已配对,那么由配对的电子的自旋产生的小 磁场两两大小相等、方向相反,磁效应互相抵消,净磁场等于0, 若将这种物质放在外磁场中,在其作用下,就要产生一个与外 磁场方向相反的诱导磁矩而受到外磁场的排斥,因此,没有未 成对电子的原子、分子或离子都具有抗磁性;如果物质具有未 成对电子,则由单电子的自旋产生的小磁场不能被抵消,净磁 场不等于0,则该物质具有顺磁性,这种物质在外磁场中,不仅 产生一个与外磁场方向相反的诱导磁矩,而且它的分子磁矩还 沿磁场方向取向,由于分子磁矩比诱导磁矩要大得多,总的结 果是产生了与磁场方向一致的磁矩,因而受到外磁场的吸引, 因此,具有未成对电子的物质大都具有顺磁性
分子中的电子在绕核的轨道运动和电子本身的自旋运动都 会产生磁效应。电子自旋运动产生自旋角动量, 从而产生自旋 磁矩;电子的轨道运动产生的轨道角动量, 产生轨道磁矩。当 把分子作为一个整体看时, 构成分子的各个电子对外界产生的 磁效应的总和可用一个等效的环电流(称为分子电流)表示, 这 个环电流具有一定的磁矩, 称为分子磁矩。在多数情况下, 分 子磁矩主要是由电子自旋产生的。如果物质的原子或分子轨道 中, 所有的电子都已配对, 那么由配对的电子的自旋产生的小 磁场两两大小相等、方向相反, 磁效应互相抵消, 净磁场等于0, 若将这种物质放在外磁场中, 在其作用下, 就要产生一个与外 磁场方向相反的诱导磁矩而受到外磁场的排斥, 因此, 没有未 成对电子的原子、分子或离子都具有抗磁性;如果物质具有未 成对电子, 则由单电子的自旋产生的小磁场不能被抵消, 净磁 场不等于0, 则该物质具有顺磁性, 这种物质在外磁场中, 不仅 产生一个与外磁场方向相反的诱导磁矩, 而且它的分子磁矩还 沿磁场方向取向, 由于分子磁矩比诱导磁矩要大得多, 总的结 果是产生了与磁场方向一致的磁矩, 因而受到外磁场的吸引, 因此, 具有未成对电子的物质大都具有顺磁性

二兹矩的计算 (一)纯自旋磁矩 在多数情况下,分子磁矩主要是由电子的自旋产生的,纯的 自旋磁矩可根据总自旋量子数进行计算。 Hs=g/S(S+1) 其中$为总自旋量子数,等于未成对电子数的一半,g为朗德 因子,对于自由电子,g=2.0023,通常取g=2,于是上式变为: u三√n(n+2) 式中为未成对电子数。这个式子表明,如果忽略了轨道角 动量对磁矩的贡献,可由磁矩直接计算出某种离子的未成对电 子数。 按这个公式算出来的磁矩,在少数情况下与实验值不一致, 这正是由于忽略了未成对电子的轨道运动对磁矩的贡献之故
二 磁矩的计算 (一) 纯自旋磁矩 在多数情况下, 分子磁矩主要是由电子的自旋产生的, 纯的 自旋磁矩可根据总自旋量子数进行计算。 s =g 其中S为总自旋量子数, 等于未成对电子数的一半, g为朗德 因子, 对于自由电子, g=2.0023, 通常取g=2, 于是上式变为: s = 式中n为未成对电子数。这个式子表明, 如果忽略了轨道角 动量对磁矩的贡献, 可由磁矩直接计算出某种离子的未成对电 子数。 按这个公式算出来的磁矩, 在少数情况下与实验值不一致, 这正是由于忽略了未成对电子的轨道运动对磁矩的贡献之故。 n(n + 2) S(S+1)

(二)轨道磁性对磁矩的贡献 如果加上轨道磁性对磁矩的贡献,则磁矩的计算公式变为: us+L=V4S(S+1)+L(L+1) 按照这个公式计算出来的磁矩在大多数情况下也与实验值 不一致。表明在多数情况下,轨道角动量对分子磁矩的贡献很 小或没有贡献。 研究表明:轨道角动量对分子磁矩是否有贡献取决 于外磁场改变时电子能否自旋平行地在不同轨道之间 再分配。这种分配必须在对称性相同的能级之间进行
(二) 轨道磁性对磁矩的贡献 如果加上轨道磁性对磁矩的贡献,则磁矩的计算公式变为: S+L = 4S(S+1) +L(L+1) 研究表明:轨道角动量对分子磁矩是否有贡献, 取决 于外磁场改变时电子能否自旋平行地在不同轨道之间 再分配。这种分配必须在对称性相同的能级之间进行。 按照这个公式计算出来的磁矩在大多数情况下也与实验值 不一致。表明在多数情况下, 轨道角动量对分子磁矩的贡献很 小或没有贡献

在八面体场中,d轨道分裂为tg和eg,由于eg轨道是 由形状不相同的两个简并轨道组成的,两条轨道的对 称性不同,电子不能在这两条轨道中进行自旋平行的 再分配,所以对磁矩不能作出贡献;但2轨道是由对称 性和形状都完全相同的dy、dz、dz所组成,电子可以 在这三条轨道中进行自旋平行的再分配,因而能对磁 矩作出贡献。但是当三条轨道各被一个或两个电子占 据时,这种再分配不能进行,所以半满和全满的2轨道 的磁矩也被冻结。相反,2g、2g2、t2g4、t2g,由于对同 一自旋方向的电子来说,还存在有空轨道,因而能进行 自旋平行的再分配,所以可对磁矩作出贡献
在八面体场中, d轨道分裂为t2g和eg , 由于eg轨道是 由形状不相同的两个简并轨道组成的, 两条轨道的对 称性不同, 电子不能在这两条轨道中进行自旋平行的 再分配, 所以对磁矩不能作出贡献;但t2g轨道是由对称 性和形状都完全相同的dxy、dxz、dyz所组成, 电子可以 在这三条轨道中进行自旋平行的再分配, 因而能对磁 矩作出贡献。但是当三条轨道各被一个或两个电子占 据时, 这种再分配不能进行, 所以半满和全满的t2g轨道 的磁矩也被冻结。相反, t2g 1 、t2g 2 、t2g 4 、t2g 5 , 由于对同 一自旋方向的电子来说, 还存在有空轨道, 因而能进行 自旋平行的再分配, 所以可对磁矩作出贡献

表14轨道对八面体配合物磁矩产生的贡献 表14示出轨 道对八面体配合 八 面 体 物磁矩产生的贡 组 态 基 态 轨道贡献 献,可以发现: d ta 2T 所有能 d he 0 + 对磁矩产生 d ta nd d“高自旋 的贡献的电 tages S d“低自旋 5g4 3Tto 子组态都具 d的高自旋 te 6Ang 有T基谱项 dP低自旋 he @ 为其他基遭 d高自旋 T4 d低自旋 项的电子组 tags ng d高自旋 he 态都没有这 d”低自旋 taseg 汽 种贡献。 d tase d d tese
t2g 1 t2g 2 t2g 3 t2g 3 e g 1 t2g 4 t2g 3 e g 2 t2g 5 t2g 4 e g 2 t2g 6 t2g 5 e g 2 t2g 6 e g 1 t2g 6 e g 2 t2g 6 e g 3 表14示出轨 道对八面体配合 物磁矩产生的贡 献, 可以发现: 所有能 对磁矩产生 的贡献的电 子组态都具 有 T 基谱项, 为其他基谱 项的电子组 态都没有这 种贡献

(三)旋一轨偶合对磁性的影响 研究表明,在一些应当没有轨道磁矩贡献的物质中,如d8、d9, 他们的基谱项分别为3A2g、2E,应当没有轨道磁矩的贡献,分子磁 矩应等于由自旋产生的磁矩。然而在实际上具有这两种电子组态 的分子所产生的磁矩却比由纯自旋磁矩算出的值要大。再如4高 自旋,基态谱项为E。,也应没有轨道磁矩的贡献,但具有这种电子 组态的分子的磁矩却比纯自旋磁矩小。这是由于 自旋和轨道相互作用,即产生了旋一轨偶合使得 一定量的激发江谱顶湿到了基谱顶之中,从而产生轨 道磁矩贡献之放。 般说来,对于第一过渡系的金属离子,这种偶合作用较小 可以忽略不予考虑。但对其他过渡系,镧系和锕系,这种偶合作 用较大,必须加以考虑
一般说来, 对于第一过渡系的金属离子, 这种偶合作用较小, 可以忽略不予考虑。但对其他过渡系, 镧系和锕系, 这种偶合作 用较大, 必须加以考虑。 (三) 旋-轨偶合对磁性的影响 研究表明, 在一些应当没有轨道磁矩贡献的物质中, 如d 8 、d 9 , 他们的基谱项分别为3A2g、 2Eg , 应当没有轨道磁矩的贡献, 分子磁 矩应等于由自旋产生的磁矩。然而在实际上具有这两种电子组态 的分子所产生的磁矩却比由纯自旋磁矩算出的值要大。再如d 4高 自旋, 基态谱项为5Eg , 也应没有轨道磁矩的贡献, 但具有这种电子 组态的分子的磁矩却比纯自旋磁矩小。这是由于 自旋和轨道相互作用, 即产生了旋—轨偶合使得 一定量的激发态T谱项混到了基谱项之中, 从而产生轨 道磁矩贡献之故

自由金属离子的旋一轨偶合作用可用单电子的旋轨偶合常 数Sd或多电子的旋轨偶合常数来表示,Sd与入间的关系为: 入=士Snd/n 式中n为未成对电子数,当d电子数小于5时,上式取正,大于 5时取负,等于5时,2等于0。 对于基态谱项为A或E对称性的配合物,情况比较简单,由旋 轨偶合作用引起磁矩的变化可由下式计算: er=(1一0入/△)s 其中基谱项为A2时,0=4,为A时,o=0,为E时o=2时。 例如实验测得NH4)2Ni(SO4)26HO的磁矩为3.30B.M,Ni+ (d8)有两个单电子,纯自旋磁矩为2.83B.M,在O场中,其基谱项 为3A2gc=4,查表得g=630,入=-Snd/n=-630/2=-315(d电子 多于5,入取负),Ni2+的△。=8500cm-1,于是, uer=(1-a入/△)4s =(1-4×(-315)/8500)×2.83=3.25B.M 计算结果与实验值一致
自由金属离子的旋-轨偶合作用可用单电子的旋轨偶合常 数nd或多电子的旋轨偶合常数来表示, nd与间的关系为: =± nd/n 式中n为未成对电子数, 当d电子数小于5时, 上式取正, 大于 5时取负, 等于5时, 等于0。 对于基态谱项为A或E对称性的配合物, 情况比较简单, 由旋 -轨偶合作用引起磁矩的变化可由下式计算: eff =(1- /△) s 其中基谱项为A2时, =4, 为A1时, =0 , 为E时=2时。 例如实验测得(NH4 )2Ni(SO4 )2·6H2O的磁矩为3.30B.M., Ni2+ (d8)有两个单电子, 纯自旋磁矩为2.83B.M., 在Oh场中, 其基谱项 为3A2g , =4, 查表得=630, =-nd/n=-630/2=-315 (d电子 多于5, 取负), Ni2+的△o =8500cm-1 , 于是, eff =(1- /△) s =(1-4×(-315)/8500)×2.83=3.25 B.M. 计算结果与实验值一致

单电子的偶合常数值列于下表: 过渡金属离子的单电子旋一轨偶合常数*/m Ti D Cr Mn Fe Co Ni Cu 中性原子: 70 95 135 190 275 390 比荷1+: 90 135 185 255 335 455 565 电荷2+: 123 170 230 300 400 515 630 830 电荷3+: 155 210 275 355 460 580 705 890 电荷4+: 250 355 415 520 650 790 960 Zr Nb Mo Tc Ru Rh Fd Ag 电荷1+: (300) (420) (1300) 电荷2+: (400) (610) (670) (950) (1600)(1800) 地荷3+: (500) (800) 800 (1200)(1250) 电荷4+: (850)(1300)(1400) (1700) 电荷5+: (900)(1500)(1500)(1850) Hr Ta W Rc Os Ir Pt Au 电荷1+: (3400) 地荷2+: (1500)(2100) (5000) 地荷3+: (1400)(1800)(2500)(3000) 电荷4+: (2300)(3300)(4000)(5000) 地荷5+: (2700)(3700)(4500)(5500) *括号内的值为估计值:如以J/mol为单位时,数值=表中的数值×11962
单电子的偶合常数值列于下表: