
离子性盐类溶解性的热力学讨论 1溶解过程的标准自由焓变化 离子性化合物在水中溶解的难易程度,可以根据溶解过程 的标准自由焓变化来加以讨论: △G=△H-T△S 当△G0,溶解不能自发进行,即难溶解: △G=0,溶解已处于平衡。 从上式可见,溶解过程的焓变和熵变都对自由焓变化作出 贡献,特别是溶解过程中,焓变通常很小,熵变的重要性有时 十分突出,所以在讨论溶解过程的自由焓变化时,应从△S和 △H两方面进行整体讨论。不过,一般说来,焓变的影响通常很 明显,下面着重说明熵变对自由焓变化的影响
离子性盐类溶解性的热力学讨论 1 溶解过程的标准自由焓变化 离子性化合物在水中溶解的难易程度,可以根据溶解过程 的标准自由焓变化来加以讨论: △G=△H-T△S 当△G 0,溶解不能自发进行,即难溶解; △G=0,溶解已处于平衡。 从上式可见,溶解过程的焓变和熵变都对自由焓变化作出 贡献,特别是溶解过程中,焓变通常很小,熵变的重要性有时 十分突出,所以在讨论溶解过程的自由焓变化时,应从△S和 △H两方面进行整体讨论。不过,一般说来,焓变的影响通常很 明显,下面着重说明熵变对自由焓变化的影响

溶解过程中的熵变包括两个方面: (1)在离子化合物溶解生成水合离子的过程中,由于离子的 电荷强电场的作用,使得在离子周围形成了一个水化层。显然, 水化过程使系统的混乱度减小。 (2)离子的水化破坏了水的簇团结构,使水分子变得自由, 结果是体系混乱度增加,水合熵增加。 因此,溶解过程的熵是增加还是减小决定于这两个方面哪 一个占优势。 显然,当离子的电荷很高和离子半径较小时,离子的电荷 密度较大,第一种效应显然占优势,此时熵值减小,不利于溶 解过程的发生;相反,当离子电荷低、半径大、离子电荷密度 小,此时,第一种效应较弱,此时熵值增加,有利于溶解过程 的进行。 总的说来,当△S0,熵变顶对自由焓变化 的贡献是负值,即△S>O,使盐的溶解性增加
溶解过程中的熵变包括两个方面: (1) 在离子化合物溶解生成水合离子的过程中,由于离子的 电荷强电场的作用,使得在离子周围形成了一个水化层。显然, 水化过程使系统的混乱度减小。 (2) 离子的水化破坏了水的簇团结构,使水分子变得自由, 结果是体系混乱度增加,水合熵增加。 因此,溶解过程的熵是增加还是减小决定于这两个方面哪 一个占优势。 显然,当离子的电荷很高和离子半径较小时,离子的电荷 密度较大,第一种效应显然占优势,此时熵值减小,不利于溶 解过程的发生;相反,当离子电荷低、半径大、离子电荷密度 小,此时,第一种效应较弱,此时熵值增加,有利于溶解过程 的进行。 总的说来,当△S0,熵变项对自由焓变化 的贡献是负值,即△S>0,使盐的溶解性增加
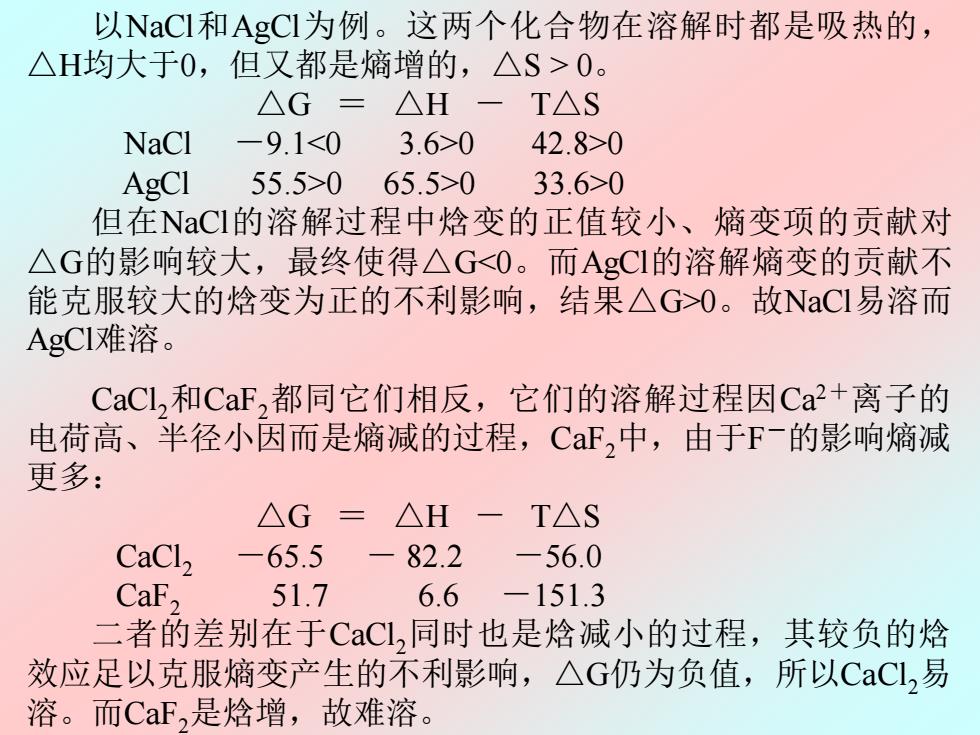
以NaCI和AgCI为例。这两个化合物在溶解时都是吸热的, △H均大于0,但又都是熵增的,△S>0。 △G=△H-T△S NaCl-9.10 42.8>0 AgCl 55.5>065.5>0 33.6>0 但在NaCI的溶解过程中焓变的正值较小、熵变项的贡献对 △G的影响较大,最终使得△G0。故NaCI易溶而 AgCI难溶。 CaCl,和CaF,都同它们相反,它们的溶解过程因Ca+离子的 电荷高、半径小因而是熵减的过程,CF,中,由于F-的影响熵减 更多: △G=△H -T△S CaCl, -65.5 一 82.2 -56.0 CaF, 51.7 6.6 -151.3 二者的差别在于CaCl,同时也是焓减小的过程,其较负的焓 效应足以克服熵变产生的不利影响,△G仍为负值,所以CaCL,易 溶。而CaF,是焓增,故难溶
以NaCl和AgCl为例。这两个化合物在溶解时都是吸热的, △H均大于0,但又都是熵增的,△S > 0。 △G = △H - T△S NaCl -9.10 42.8>0 AgCl 55.5>0 65.5>0 33.6>0 但在NaCl的溶解过程中焓变的正值较小、熵变项的贡献对 △G的影响较大,最终使得△G0。故NaCl易溶而 AgCl难溶。 CaCl2和CaF2都同它们相反,它们的溶解过程因Ca2+离子的 电荷高、半径小因而是熵减的过程,CaF2中,由于F-的影响熵减 更多: △G = △H - T△S CaCl2 -65.5 - 82.2 -56.0 CaF2 51.7 6.6 -151.3 二者的差别在于CaCl2同时也是焓减小的过程,其较负的焓 效应足以克服熵变产生的不利影响,△G仍为负值,所以CaCl2易 溶。而CaF2是焓增,故难溶

2溶解过程的热力学分析 为了探讨离子性盐溶解自由焓变化的某些规律,先建立一个热力学 循环: M.X,(s) △GCM+(aq) +ax(aq) △atmGm99 IⅡ△Gm9 →cMa+(g) 十 ax(g) △sGm9=△latGmo+△hGm9 也就是说,溶解过程的自由焓变化,包括破坏晶体晶格和离 子水合两个过程的自由焓变化。对于破坏晶体晶格过程: M.X (s)-cMa(aq)+axc-(aq) △aGno=△atHm-T△SiatSm9 L(McXa)-T△1atSm9 1079×105(a+c22-T△amS. r++r_ △arSm9=112.6(a十cJ-k-lmol-1 △atGm 1079×10(ac2r2-31.1a+c)kJmol-
2 溶解过程的热力学分析 为了探讨离子性盐溶解自由焓变化的某些规律,先建立一个热力学 循环: McXa (s) cMa+(aq) + aXc-(aq) I Ⅱ cMa+(g) + aXc-(g) △SGm θ =△latGm θ +△hGm θ 也就是说,溶解过程的自由焓变化,包括破坏晶体晶格和离 子水合两个过程的自由焓变化。对于破坏晶体晶格过程: McXa (s) cMa+(aq)+aXc-(aq) △latGm θ=△latHm θ-T△latSm θ ≈L(McXa )-T△latSm θ = -T△latSm θ △latSm θ=112.6(a+c)J·k-1·mol-1 △latGm θ= -31.1(a+c) kJ·mol-1 △SGm θ △latmGm θ △hGm θ 1.079×105 (a+c)Z+Z- r++r- 1.079×105 (a+c)Z+Z- r++r-

由此式可见: ①破坏晶体,即使之成为无限远离的气态离子,其熵变大 于0,即破坏晶体晶格的熵效应对溶解有利。 ②△latHm~L>0,破坏晶体需耗能,此项对溶解是不利的。 对于水合过程:cMa+(g)十aXc-(g)→cMa+(aq)+aXc-(aq) △hGnf=△hHm9-T△hSm9 ①离子水合是一个放热过程,△Hm<0,即负的水合焓有 利于溶解过程进行; ②水合熵△Sm9=Sm(aq)-Sm(g)<0,即熵效应不利于溶解。 综合以上两个过程: △sGm9=△latGm+△hGne =(△latHm9+△Hn)-T(△latSm+△hSm) =△,Hmf-T△Sm9 可见,溶解自由焓变取决于溶解焙效应和溶解熵效应两顶
由此式可见: ① 破坏晶体,即使之成为无限远离的气态离子,其熵变大 于0,即破坏晶体晶格的熵效应对溶解有利。 ② △latHm≈L>>0,破坏晶体需耗能,此项对溶解是不利的。 综合以上两个过程: △sGm θ=△latGm θ+△hGm θ =(△latHm θ+△hHm θ )-T(△latSm θ+△h Sm θ ) =△sHm θ-T△s Sm θ 对于水合过程:cMa+(g)+aXc-(g) cMa+(aq)+aXc-(aq) △hGm θ=△hHm θ-T△h Sm θ ① 离子水合是一个放热过程,△hHm θ<0,即负的水合焓有 利于溶解过程进行; ② 水合熵△h Sm θ=Sm θ (aq)-Sm θ (g)<0,即熵效应不利于溶解。 可见,溶解自由焓变取决于溶解焓效应和溶解熵效应两项

综上:在溶解焓中,由于包括了晶格焓和水合焓两项, 晶格焓大于0,吸收热量;水合焓小于0,放出热量。溶 解时究竟是吸热还是放热,取决于这两项的相对大小。 对于某特定晶体来说,这两项,即晶格能和水合焓通常 为很接近的两个大的数值,因而使得很多晶体的溶解焓 △,H常常是一个小的数值。即盐类晶体溶解热效应较小, 这时溶解熵所起的作用就显得十分重要。这从前面介绍 过的NaCI的溶解情况就可看到这一点。 溶解熵变也包括两部分,晶格熵和水合熵。其中晶格 熵大于0,水合熵小于0,溶解熵变是增加还是减小,取决 于二者的相对大小
综上:在溶解焓中,由于包括了晶格焓和水合焓两项, 晶格焓大于0,吸收热量;水合焓小于0,放出热量。溶 解时究竟是吸热还是放热,取决于这两项的相对大小。 对于某特定晶体来说,这两项,即晶格能和水合焓通常 为很接近的两个大的数值,因而使得很多晶体的溶解焓 △sHm θ常常是一个小的数值。即盐类晶体溶解热效应较小, 这时溶解熵所起的作用就显得十分重要。这从前面介绍 过的NaCl的溶解情况就可看到这一点。 溶解熵变也包括两部分,晶格熵和水合熵。其中晶格 熵大于0,水合熵小于0,溶解熵变是增加还是减小,取决 于二者的相对大小

下面以一些盐作为例子看一下溶解熵变的情况。 ①「+较大,z较小,如K+盐 K+离子是一个较大的一价阳离子,若阴离子亦为一价,且 有较大半径,则这些盐在溶解时总是△arSm0,而△Sm虽然小 于0,但对一价较大的离子来说,水化程度低,熵减幅度小,即 △atSm正值大、占优势,△hSm负值小, 影响不显著,因而晶格 熵增未能被水化熵减所抵消,结果是△.Sm成为正值。即总体说 来,溶解时是熵增的。因此,尽管不少的钾盐的△H为正值 (正值表明△Hm正值绝对值大,△Hm负值绝对值小),似乎对 溶解不利,但却因△S也为正值而导致易溶。 ②r大,乙_小,高氯酸盐、硝酸盐 一价的半径大的一些阴离子(如NO3ˉ、CIO4)的盐类,常由 于较正的△,Sm而导致易溶,尤其是当△H为负时更是如此。 已知硝酸盐都是易溶的,高氯酸盐也有不少是易溶的。 (可参照①r+较大,z+较小的情况进行讨论)
① r+较大,z+较小,如K+盐 K+离子是一个较大的一价阳离子,若阴离子亦为一价,且 有较大半径,则这些盐在溶解时总是△latSm θ>0,而△h Sm θ虽然小 于0,但对一价较大的离子来说,水化程度低,熵减幅度小,即 △latSm θ正值大、占优势,△h Sm θ负值小,影响不显著,因而晶格 熵增未能被水化熵减所抵消,结果是△s Sm θ成为正值。即总体说 来,溶解时是熵增的。因此,尽管不少的钾盐的△sHm θ为正值 (正值表明△latHm θ正值绝对值大,△hHm θ负值绝对值小),似乎对 溶解不利,但却因△s Sm θ也为正值而导致易溶。 ② r-大,z-小,高氯酸盐、硝酸盐 一价的半径大的一些阴离子(如NO3 -、ClO4 -)的盐类,常由 于较正的△s Sm θ而导致易溶,尤其是当△sHm θ为负时更是如此。 已知硝酸盐都是易溶的,高氯酸盐也有不少是易溶的。 (可参照① r+较大,z+较小的情况进行讨论) 下面以一些盐作为例子看一下溶解熵变的情况

③r-大,z+大(如碳酸盐) 碳酸盐同硝酸盐相比,阴离子半径相近[r(C032-)=185pm, r(NO3)=189pm,但电荷多了一倍,水化程度升高,△Sm减 小幅度增加,破坏晶格的熵增能被水合熵减所抵消,结果是溶 解熵减小,即△,Sm为负值。因此,尽管不少碳酸盐的△H为 负值(如Mg2+、Ca2+、Sr2+),但却难于溶解。 ④Z+大,z_大(如镧系磷酸盐) 当阴阳离子均为高价时(如镧系元素的磷酸盐),由于电荷高, 水化熵占优势,使得其溶解熵△S负值更大,均为难熔盐。即 使是由一价阴离子F一组成的高价阳离子盐也不例外。 最后需要强调的是,以△,Gm>0或<0作为易溶或难溶的分界 线并不十分确切,如<SO Na2S04,其△,Gm均大于0,但都 是易溶的
③ r-大,z+大(如碳酸盐) 碳酸盐同硝酸盐相比,阴离子半径相近[r(CO3 2-)=185 pm, r(NO3 -)=189 pm],但电荷多了一倍,水化程度升高,△h Sm θ减 小幅度增加,破坏晶格的熵增能被水合熵减所抵消,结果是溶 解熵减小,即△s Sm θ为负值。因此,尽管不少碳酸盐的△sHm θ为 负值(如Mg2+ 、Ca2+ 、Sr2+),但却难于溶解。 ④ z+ 大,z-大(如镧系磷酸盐) 当阴阳离子均为高价时(如镧系元素的磷酸盐),由于电荷高, 水化熵占优势,使得其溶解熵△s Sm θ负值更大,均为难熔盐。即 使是由一价阴离子F-组成的高价阳离子盐也不例外。 最后需要强调的是,以△sGm θ>0或<0作为易溶或难溶的分界 线并不十分确切,如K2 SO4、Na2 SO4,其△sGm θ均大于0,但都 是易溶的

3近似处理 在通常的概念中,盐类溶解量达到0.01olL-1时就认为是 易溶的,溶解量小于0.01olL-1就认为是微溶或难溶的。这个 界限可作为近似处理的依据。 ★对于1一1价或2一2价型的盐 MX(s)-Mn+(aq)+Xn-(aq) (n=1或2) Kp=Mm+][Xm-]=0.012=1×10-4 AoGm=-RTInKsp=22.8 kJ-mol-1 △Gm22.8 kJmol-1属难溶盐, 此时Kp10-4,或溶解度>0.01molL-1; 因此,某一个1-1价或2-2价的盐△oGm以22.8 kJ-mol-1 作为判断的依据,若△oGm22.8 kJmol-属难溶盐,此时Kp10-4,或溶解度>0.01moL-1
3 近似处理 在通常的概念中,盐类溶解量达到0.01 mol·L-1时就认为是 易溶的,溶解量小于0.01 mol·L-1就认为是微溶或难溶的。这个 界限可作为近似处理的依据。 ★ 对于1-1价或2-2价型的盐 MX(s) Mn+(aq)+Xn-(aq) (n=1或2) Ksp =[Mn+][Xn-]=0.012=1×10-4 △solGm θ=-RTlnKsp =22.8 kJ·mol-1 △solGm θ>22.8 kJ·mol-1属难溶盐, 此时Ksp 10-4 ,或溶解度 > 0.01 mol·L-1; 因此,某一个1-1价或2-2价的盐△solGm θ以 22.8 kJ·mol-1 作为判断的依据,若△solGm θ>22.8 kJ·mol-1属难溶盐,此时Ksp 10-4 ,或溶解度>0.01 mol·L-1

★对于1一2价或2一1价型的盐 MX,(MX)(s)→M2+(2M+)(aq)+2X-(X2-)(aq) Kp=[MP+][X-]2(或[M+]2[X2-j)=0.01×0.022(或0.022×1) =4×106 △,Gm6=-RTInKsp=30.80 kJ.mol-1 △oGm>30.8 kJmol-1属难溶盐, 此时Kp4×10-6,或溶解度>0.01moL-1 因此,某1一2价或2-1价型的盐,△oGm38.5 kJ.mol-1以 作为判断的依据,若△Gm38.5 kJ.mol-属难溶盐,此时Kp2.7×10-7,或溶解度>0.01molL-1。 ★类似地,可计算出1一3或3-1型盐的△oGm界限值为38.5 molL-1。 ★2-3或3-2型盐的△Gm界限值为45.6 kJmol-1
★ 类似地, 可计算出1-3或3-1型盐的△solGm θ界限值为38.5 mol·L-1 。 ★ 2-3或3-2型盐的△solGm θ界限值为45.6 kJ·mol-1 。 ★ 对于1-2价或2-1价型的盐 MX2 (M2X)(s) M2+(2M+)(aq)+2X-(X2-)(aq) Ksp =[M2+][X-] 2 (或[M+] 2 [X2-])=0.01×0.022 (或0.022×1) =4×106 △sGm θ =-RTlnKsp =30.80 kJ·mol-1 △solGm θ>30.8 kJ·mol-1属难溶盐, 此时Ksp 4×10-6 ,或溶解度 >0.01 mol·L-1 因此,某1-2价或2-1价型的盐,△solGm θ38.5 kJ·mol-1以 作为判断的依据,若△solGm θ>38.5 kJ·mol-1属难溶盐,此时Ksp 2.7×10-7 ,或溶解度 >0.01 mol·L-1