
第四章 多组分系统热力学 71 6.15%
第四章 多组分系统热力学
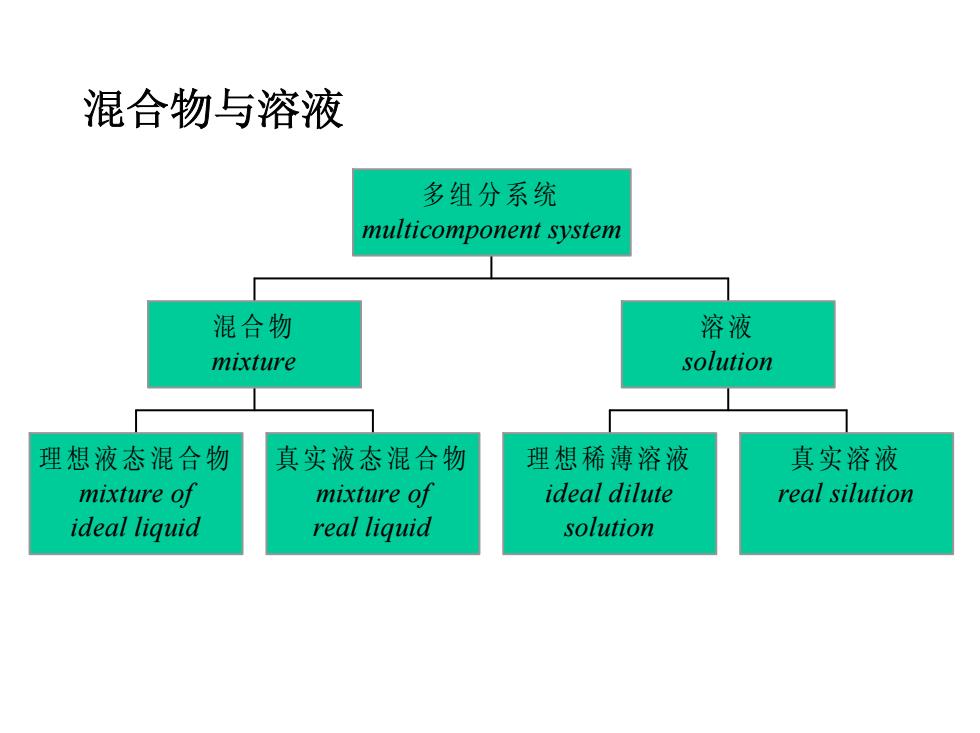
混合物与溶液 多组分系统 multicomponent system 混合物 溶液 mixture solution 理想液态混合物 真实液态混合物 理想稀薄溶液 真实溶液 mixture of mixture of ideal dilute real silution ideal liquid real liquid solution
混合物与溶液 理想液态混合物 mixture of ideal liquid 真实液态混合物 mixture of real liquid 混合物 mixture 理想稀薄溶液 ideal dilute solution 真实溶液 real silution 溶 液 solution 多组分系统 multicomponent system
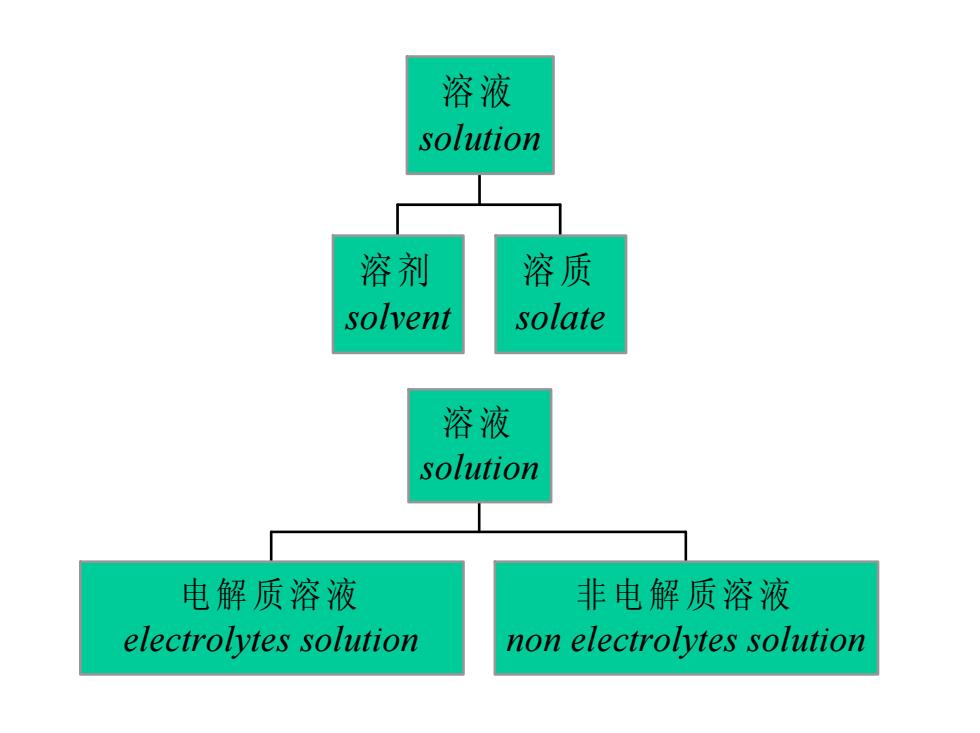
溶液 solution 溶剂 溶质 solvent solate 溶液 solution 电解质溶液 非电解质溶液 electrolytes solution non electrolytes solution
溶 剂 solvent 溶 质 solate 溶 液 solution 电解质溶液 electrolytes solution 非电解质溶液 non electrolytes solution 溶 液 solution

4.1偏摩尔量 对单组分系统,物质B的物质的量为nB, B的摩尔体积(nolar volume) def m,B ng B的摩尔热力学能(molar thermodynamic energy) def U ns B的摩尔焓(molar enthalpy) def H ns
4.1 偏摩尔量 对单组分系统,物质B的物质的量为nB, B的摩尔体积(molar volume) B m,B def ══ n V V ∗ B的摩尔热力学能(molar thermodynamic energy) B m,B def ══ n U U∗ B的摩尔焓(molar enthalpy) B m,B def ══ n H H ∗

B的摩尔熵(molar entropy) def S ne B的摩尔亥姆霍兹函数(molar Helmholz function) def A ng B的摩尔吉布斯函数(molar Gibbs function) def G m.B B
B m,B def ══ n S S B的摩尔熵 ∗ (molar entropy) B的摩尔亥姆霍兹函数(molar Helmholz function) B m,B def ══ n A A∗ B的摩尔吉布斯函数(molar Gibbs function) B m,B def ══ n G G∗

4.1.1问题的提出 例如,在25℃、101.325kPa时, 18.07cm3H0)+5.74cm3CH3CH20H() =23.30cm3(HO+CH3CH0H,1) 23.81 cm3(H2O+CHCH,OH,1) V nAVA nBVB
4.1.1 问题的提出 例如,在25℃、101.325kPa时, 18.07cm3 H2O(l)+5.74 cm3CH3CH2OH(l) =23.30 cm3(H2O+CH3CH2OH,l) ≠23.81 cm3(H2O+CH3CH2OH,l) ∗ ∗ V ≠ nAVA + nBVB

4.1.2偏摩尔量 对于一个均相多组分系统(混合物或溶液), Z=f(T,p,nA,ng’.) dz=(z /8)p.ncdT-(oZ/op).ncdp +(Z/amA),pmC,c≠AdnA十(Z/dnE)z,pmc, C≠BdnB+. =(oZ/OT)p.n(cdT(oZ op),mcdp+B(Z/ OnB),p,nC,C≠BdnB
4.1.2 偏摩尔量 对于一个均相多组分系统(混合物或溶液) , Z=f (T,p,nA,nB,.) dZ=(∂Z/∂T)p,n(C)dT+(∂Z/∂p)T,n(C)dp +(∂Z/∂nA)T,p,n(C,C≠A)dnA+(∂Z/∂nB)T,p,n(C, C≠B)dnB+. =(∂Z/∂T)p,n(C)dT+(∂Z/∂p)T,n(C)dp+∑B(∂Z/ ∂nB)T,p,n(C,C≠B)dnB

偏摩尔量(partial molar quantit): def aZ onB )Tp.n(C.C+B) dz=(z/8n)p.ncdT+(oz/ap)1.n(cdp ZAdnA+ZednB十. =(oZ/aD).mcdT+(oZ/op).mcdp ∑BZpdnB
偏摩尔量(partial molar quantity): B , , ( ) C,C B B def ══ ≠ ⎟⎟⎠⎞ ⎜⎜⎝⎛ ∂∂ T p n nZ Z dZ=(∂Z/∂T)p,n(C)dT+(∂Z/∂p)T,n(C)dp+ ZAdnA+ZBdnB+. =(∂Z/∂T)p,n(C)dT+(∂Z/∂p)T,n(C)dp+ ∑BZBdnB

B的偏摩尔体积(partial molar volume) def av OnBr,pmc,C≠B) B的偏摩尔热力学能(partial molar thermodynamic energ)) def UR- au one )r.p.(C.C+B) B的偏摩尔焓(partial molar enthalpy) def OH One )r.p.n(C.C+B)
B 的偏摩尔体积 (partial molar volume ) B , , ( ) C,C B B def ══ ≠ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ∂ ∂ T p n n V V B 的偏摩尔热力学能 (partial molar thermodynamic energy ) B , , ( ) C,C B B def ══ ≠ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ∂ ∂ T p n n U U B 的偏摩尔焓 (partial molar enthalpy ) B , , ( ) C,C B B def ══ ≠ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ∂ ∂ T p n n H H

B的偏摩尔熵(partial molar entropy) def as Se Ong ).p.(C.C+B) B的偏摩尔亥姆霍兹函数(partial molar Helmholz function) def A ong )r.p.(C.C+B) B的偏摩尔吉布斯函数(partial molar Gibbs function) def aG OnB1,p,nc,c≠B)
B的偏摩尔熵(partial molar entropy) B , , ( ) C,C B B def ══ ≠ ⎟⎟⎠⎞ ⎜⎜⎝⎛ ∂∂ T p n nS S B的偏摩尔亥姆霍兹函数(partial molar Helmholz function) B , , ( ) C,C B B def ══ ≠ ⎟⎟⎠⎞ ⎜⎜⎝⎛ ∂∂ T p n nA A B的偏摩尔吉布斯函数(partial molar Gibbs function) B , , ( ) C,C B B def ══ ≠ ⎟⎟⎠⎞ ⎜⎜⎝⎛ ∂∂ T p n nG G