
界面现象 Interface Phenomenon
界面现象 Interface Phenomenon

10.1界面现象研究的内容和方法 1、界面现象研究的内容 (1)界面层的定义 在多相系统中,相与相之间存在着 相界面,称为界面(interface) 气一液和气一固界面称为表面 (surface)
10.1 界面现象研究的内容和方法 1 、界面现象研究的内容 (1) 界面层的定义 在多相系统中,相与相之间存在着 相界面,称为界面 (interface)。 气-液和气-固界面称为表面 (surface )
(2)系统的分散度 物质分散成细小微粒的程度称为分 散度(dispersity)
(2) 系统的分散度 物质分散成细小微粒的程度称为分 散度(dispersity)

体积表面(volume surface)Ay: def A, A,= V 质量表面(nassic surface)Am: def Am m A的SI单位为ml,Am的SI单位为m2kg
体积表面 (volume surface) AV : 质量表面 (massic surface) A m : V A A V s def = m A A m s def = A V 的SI单位为 m-1 , A m 的SI单位为 m-2·kg-1

表10一11cm3立方体分散为小立方 体时系统的总表面及体积表面的变化 立方体边长1 小立方体 总表面积A 比表面A, m 数 /m2 /m1 10-2 1 6×104 6×102 103 103 6×103 6×103 104 106 6×102 6X104 105 109 6×101 6×105 10-6 1012 6 6×106 107 1015 6×10 6×107 108 1018 6×102 6X108 109 1021 6×103 6×109
表 10-1 1cm3立方体分散为小立方 体时系统的总表面及体积表面的变化 立方体边长 l /m 小立方体 数 总表面积 As /m2 比表面 Av /m-1 10-2 1 6×10-4 6×102 10-3 103 6×10-3 6×103 10-4 106 6×10-2 6×104 10-5 109 6×10-1 6×105 10-6 1012 6 6×106 10-7 1015 6×10 6×107 10-8 1018 6×102 6×108 10-9 1021 6×103 6×109

2、界面现象研究的方法 物理领域 化学领域 •胶体科学 •材料科学 生物科学 •催化化学
2、界面现象研究的方法 •物理领域 •化学领域 •胶体科学 •材料科学 •生物科学 •催化化学

10.2表面张力与单位表面吉布斯函数 1、表面功及表面张力 在温度、压力和组成恒定时,可 逆地使表面积增加dA、,环境对系统做 的功,称为表面功(surface work) δW=odAs 表面张力(surface tention)或界面张力 (interfacial tension 表面张力o的SI单位为Jm2
10.2 表面张力与单位表面吉布斯函数 1、表面功及表面张力 在温度、压力和组成恒定时,可 逆地使表面积增加dAs,环境对系统做 的功,称为表面功(surface work) δWr’=σdAs 表面张力(surface tention)或界面张力 (interfacial tension) 表面张力σ的SI单位为J·m-2

表面张力的物理意义是:当T、p 和组成恒定的条件下,增加单位表面 积时必须对系统做的可逆非体积功。 Sw' dAs )T.p.n
表面张力的物理意义是:当 T 、 p 和组成恒定的条件下,增加单位表面 积时必须对系统做的可逆非体积功。 B , , s r T p n dA W ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ′ = δ σ
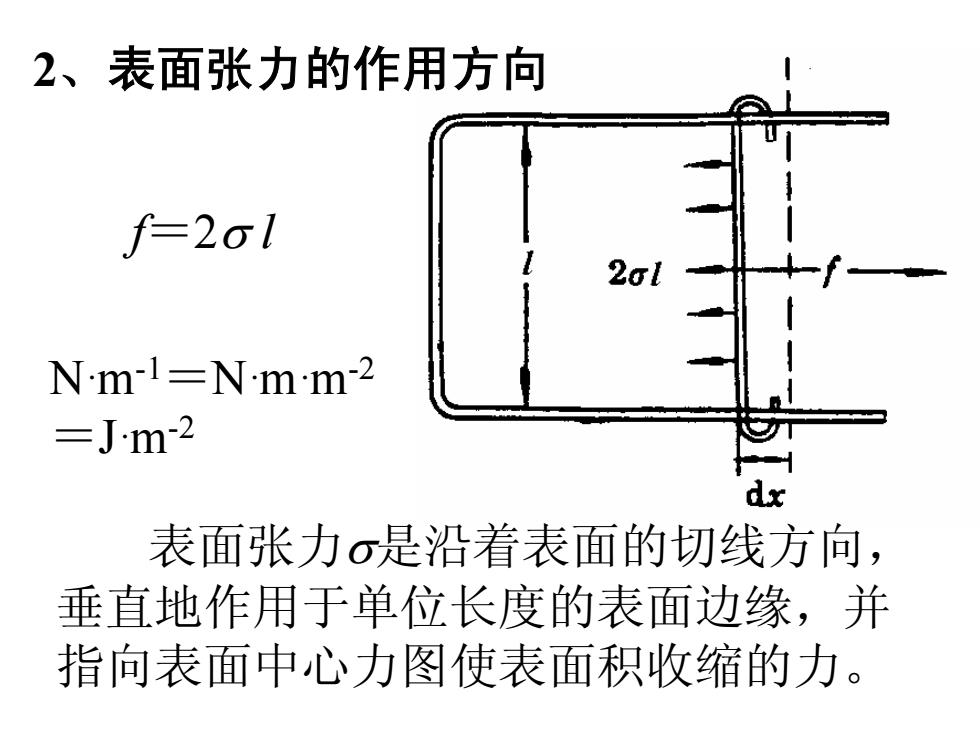
2、表面张力的作用方向 f-201 26 N'm-1=Nm'm2 =Jm2 表面张力σ是沿着表面的切线方向, 垂直地作用于单位长度的表面边缘,并 指向表面中心力图使表面积收缩的力
f=2σ l 表面张力σ是沿着表面的切线方向, 垂直地作用于单位长度的表面边缘,并 指向表面中心力图使表面积收缩的力。 2、表面张力的作用方向 N·m-1=N·m·m-2 =J·m-2

3、高度分散系统的热力学基本方程与单 位表面吉布斯函数 (1)高度分散系统的热力学基本方程 dU =TdS-pdv+o dds +adns dH=TdS+Vdp+odAs +>BednB dA=-SdT-pdv+odAs +>puadnB dG=-SdT+Vdp+odAs +>BHpdnB
3、高度分散系统的热力学基本方程与单 位表面吉布斯函数 (1) 高度分散系统的热力学基本方程 = − + S +∑B B B dU TdS pdV σ dA µ dn dH = TdS+Vdp +σ dAS +∑B µ BdnB dA = −SdT − pdV +σ dAS +∑B µ BdnB dG = −SdT +Vdp +σ dAS +∑B µ BdnB