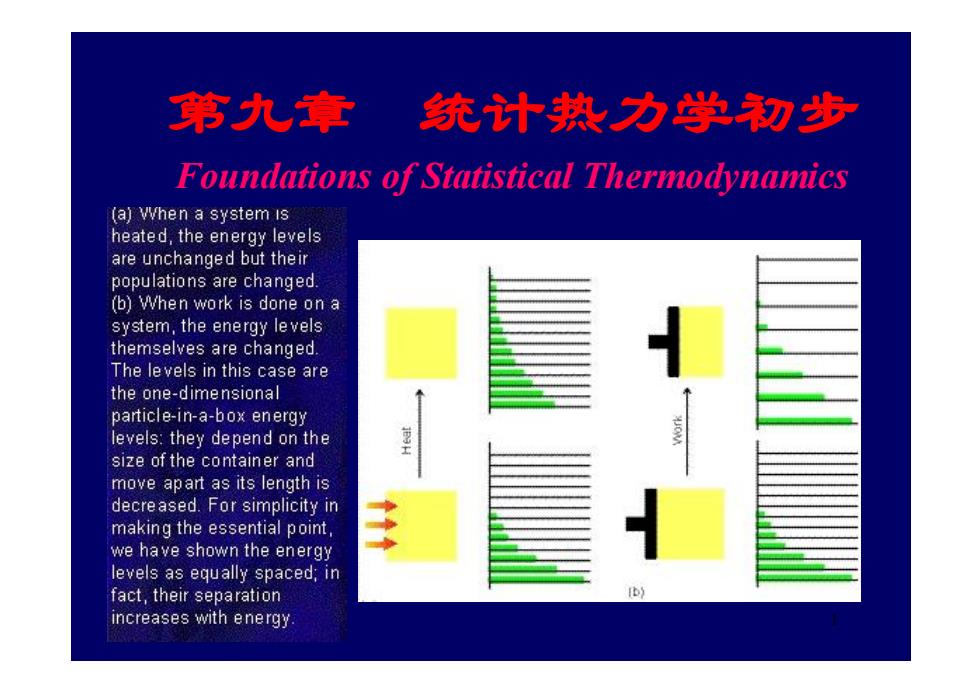
第九章 统计热力学切步 Foundations of Statistical Thermodynamics (a)When a system is heated,the energy levels are unchanged but their populations are changed. (b)When work is done on a system,the energy levels themselves are changed. The levels in this case are the one-dimensional particle-in-a-box energy levels:they depend on the size of the container and move apart as its length is decreased.For simplicity in making the essential point, we have shown the energy levels as equally spaced;in fact,their separation b increases with energy
1 第九章 统计热力学初步 Foundations of Statistical Thermodynamics

9.0统计热力学研究的内容与方法 9.0.1统计热力学研究的内容 (1)统计热力学研究的对象与任务 热力学研究的对象—含有大量粒子的宏观系统。 统计热力学研究的对象一含有大量粒子的宏观系统。 物质的宏观性质本质上是微观粒子不停地运动的 客观反应。虽然每个粒子都遵守力学定律,但是无法 用力学中的微分方程去描述整个系统的运动状态,所 以必须用统计学的方法
2 9.0 统计热力学研究的内容与方法 9.0.1 统计热力学研究的内容 ⑴统计热力学研究的对象与任务 热力学研究的对象—¾含有大量粒子的宏观系统。 统计热力学研究的对象—¾含有大量粒子的宏观系统。 物质的宏观性质本质上是微观粒子不停地运动的 客观反应。虽然每个粒子都遵守力学定律,但是无法 用力学中的微分方程去描述整个系统的运动状态,所 以必须用统计学的方法

根据对物质结构的某些基本假定,以及实验 所得的光谱数据,求得物质结构的一些基本常 数,如核间距、键角、振动频率等,从而计算分 子配分函数。再根据配分函数求出物质的热力学 性质,这就是统计热力学的基本任务。 根据统计单位的力学性质(例如速度、动 量、位置、振动、转动等),经过统计平均推求 系统的热力学性质,将系统的微观性质与宏观性 质联系起来,这就是统计热力学的研究方法。 热力学方法—宏观方法。 量子力学方法一微观方法。 统计热力学的方法一从微观到宏观的方法
3 根据统计单位的力学性质(例如速度、动 量、位置、振动、转动等),经过统计平均推求 系统的热力学性质,将系统的微观性质与宏观性 质联系起来,这就是统计热力学的研究方法。 根据对物质结构的某些基本假定,以及实验 所得的光谱数据,求得物质结构的一些基本常 数,如核间距、键角、振动频率等,从而计算分 子配分函数。再根据配分函数求出物质的热力学 性质,这就是统计热力学的基本任务。 热力学方法¾宏观方法。 量子力学方法¾微观方法。 统计热力学的方法¾从微观到宏观的方法

统计热力学方法的优点:将系统的微观性质 与宏观性质联系起来,对于简单分子计算结果常 是令人满意的。不需要进行复杂的低温量热实 验,就能求得相当准确的熵值。 统计热力学方法的局限性:计算时必须假 定结构的模型,而人们对物质结构的认识也在 不断深化,这势必引入一定的近似性。另外, 对大的复杂分子以及凝聚系统,计算尚有困 难。 4
4 统计热力学方法的优点:将系统的微观性质 与宏观性质联系起来,对于简单分子计算结果常 是令人满意的。不需要进行复杂的低温量热实 验,就能求得相当准确的熵值。 统计热力学方法的局限性:计算时必须假 定结构的模型,而人们对物质结构的认识也在 不断深化,这势必引入一定的近似性。另外, 对大的复杂分子以及凝聚系统,计算尚有困 难

9.0.2统计系统的分类 粒子一统计热力学对分子、原子等的统称。(简称子) ()按照粒子的相互作用 独立子系统 统计系统 相依子系统 独立子系统:粒子之间的相互作用非常微弱,因此 可以忽略不计,所以独立粒子系统严格讲应称为近 独立粒子系统。这种系统的总能量应等于各个粒子 能量之和,即: U=n8,+n,62+.=∑n,e 独立子系统是本章主要的研究对象 5
5 9.0.2 统计系统的分类 粒子 ¾ 统计热力学对分子、原子等的统称。(简称子) (i)按照粒子的相互作用 统计系统 独立子系统 相依子系统 { 独立子系统:粒子之间的相互作用非常微弱,因此 可以忽略不计,所以独立粒子系统严格讲应称为近 独立粒子系统。这种系统的总能量应等于各个粒子 能量之和,即: 1 1 2 2 i i i U = n e + n n e e + ××× = å 独立子系统是本章主要的研究对象

相依子系统: 相依子系统又称为非独立子系统,系统中粒子 之间的相互作用不能忽略,系统的总能量除了包括 各个粒子的能量之和外,还包括粒子之间的相互作 用的位能,即: U=∑2,6,+U(位能) 6
6 相依子系统: 相依子系统又称为非独立子系统,系统中粒子 之间的相互作用不能忽略,系统的总能量除了包括 各个粒子的能量之和外,还包括粒子之间的相互作 用的位能,即: i i i U = + ån U e (位能)
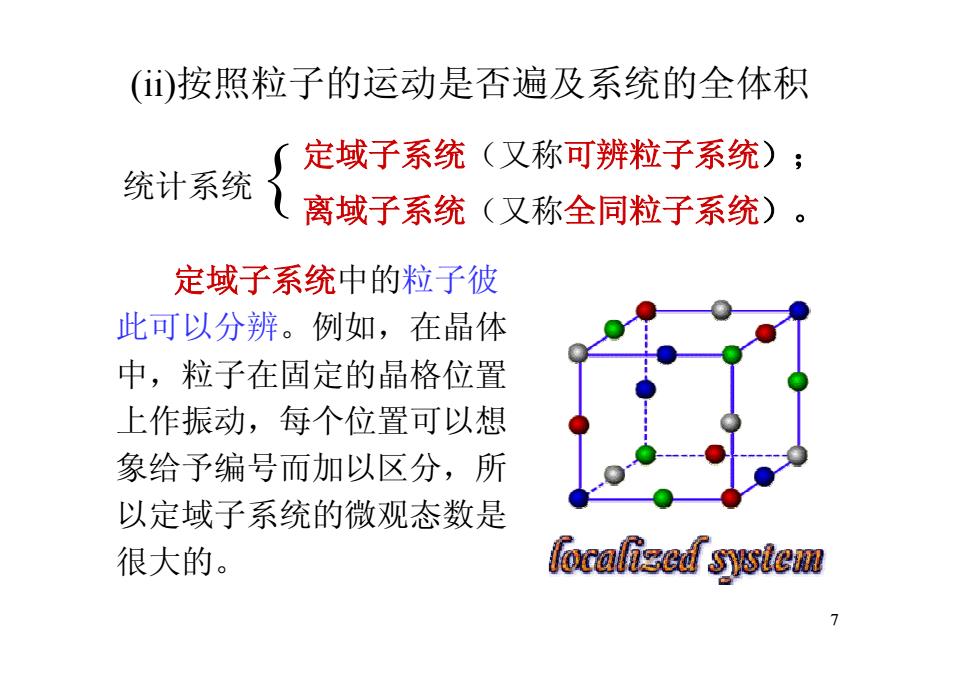
()按照粒子的运动是否遍及系统的全体积 定域子系统(又称可辨粒子系统); 统计系统 离域子系统(又称全同粒子系统)。 定域子系统中的粒子彼 此可以分辨。例如,在晶体 中,粒子在固定的晶格位置 上作振动,每个位置可以想 象给予编号而加以区分,所 以定域子系统的微观态数是 很大的。 localized system
7 (ii)按照粒子的运动是否遍及系统的全体积 统计系统 定域子系统(又称可辨粒子系统); 离域子系统(又称全同粒子系统)。 { 定域子系统中的粒子彼 此可以分辨。例如,在晶体 中,粒子在固定的晶格位置 上作振动,每个位置可以想 象给予编号而加以区分,所 以定域子系统的微观态数是 很大的

离域子系统: 离域子系统,基本粒 子之间不可区分。例如, 气体的分子,总是处于混 乱运动之中,彼此无法分 辨,所以气体是离域子系 统,它的微观状态数在粒 子数相同的情况下要比定 mon-bosalized syslem 域子系统少得多。 8
8 离域 子 系统: 离域 子系统 , 基 本 粒 子之间不可 区 分 。例如 , 气体 的 分子,总是 处 于 混 乱运动 之中, 彼 此 无法分 辨,所以气体 是离域子系 统, 它 的微观状态数在 粒 子 数 相 同 的 情况下 要比定 域子系统少得多

9.0.3统计热力学的分类 目前,统计主要有三种: 一种是Maxwel-Boltzmann统计,通常称为Boltzmann:统计。 1900年Planck提出了量子论,引入了能量量子化 的概念,发展成为初期的量子统计。 在这时期中,Boltzmann有很多贡献,开始是用经典 的统计方法,而后来又有发展,加以改进,形成了目前 的Boltzmann统计。 1924年以后有了量子力学,使统计力学中力学的基 础发生改变,随之统计的方法也有改进,从而形成了Bos -Einstein统计和Fermi-Dirac:统计,分别适用于不同系统。 但这两种统计在一定条件下通过适当的近似, 可与Boltzmann:统计得到相同结果
9 9.0.3 统计热力学的分类 目前,统计主要有三种: 一种是Maxwell-Boltzmann统计,通常称为Boltzmann统计。 1900年Planck提出了量子论,引入了能量量子化 的概念,发展成为初期的量子统计。 在这时期中,Boltzmann有很多贡献,开始是用经典 的统计方法,而后来又有发展,加以改进,形成了目前 的Boltzmann统计。 1924年以后有了量子力学,使统计力学中力学的基 础发生改变,随之统计的方法也有改进,从而形成了Bose -Einstein 统计和Fermi-Dirac统计,分别适用于不同系统。 但这两种统计在一定条件下通过适当的近似, 可与Boltzmann统计得到相同结果

9.1能级分布、状态分布 9.1.1系统及粒子的微观状态 量子态和微观状态数 对定域孤立分子,薛定谔(Schrodinger)方程: Hy=eΨ 本征函数y1、2 本征值81、82、3、. 系统任何一个可到达的(物理上可能的)量子态 称为该系统的微观状态。 10
10 9.1 能级分布、状态分布 9.1.1 系统及粒子的微观状态 量子态和微观状态数 对定域孤立分子,薛定谔(Schrodinger)方程: H ˆ y = ey 本征函数y1、y2、y3、. 本征值e1 、e2 、e3 、. 系统任何一个可到达的(物理上可能的)量子态 称为该系统的微观状态