
§2-2分布系数、副反应系数及条件平衡常数 分析化学所面临的是控制怎样的介质条件使 被测物按着即定的反应定量完成,同时尽可能使 共存组分不参与反应。所面对的体系中有多种平 衡同时存在,提出了处理平衡问题的新方法。 一、分析浓度与平衡浓度 分析浓度:某物质在溶液中存在各种型体平衡浓度 之和。用C表示。 在分析体系中常有各种电解质,加入试剂或被测物 时,不是以单一的型体存在
§2-2 分布系数、副反应系数及条件平衡常数 分析化学所面临的是控制怎样的介质条件使 被测物按着即定的反应定量完成,同时尽可能使 共存组分不参与反应。所面对的体系中有多种平 衡同时存在,提出了处理平衡问题的新方法。 一、分析浓度与平衡浓度 分析浓度:某物质在溶液中存在各种型体平衡浓度 之和。用c 表示。 在分析体系中常有各种电解质,加入试剂或被测物 时,不是以单一的型体存在

如HAc在水中有HAc,Ac 总浓度cAe=HAd+[AC] H3A在水中 CA=CHA=[H3A]+[H2A]+[HA]+[A] 将M加入到含有配体X的体系内 CM [M][MX][MX2][MX3][MX4]
如 HAc在水中有HAc,Ac- 总浓度 cHAc = [HAc] + [Ac-] H3A在水中 cA = = [H3A] + [H2A] + [HA] + [A] 将 M加入到含有配体X的体系内 cM = [M] + [MX] + [MX2] + [MX3] + [MX4] H3A c

如果M与A进行滴定反应,称主反应 M+A≌MA 将HA和M同时引入含X的体系,则 CA=[H3A]+[H2A]+[HA]+[A]+[MA] CM [M]+[MX]+[MX2]+[MX3][MX4]+[MA] 将除产物MA以外的平衡浓度的总和记为[A']和[M'] [A]=[HA]+H2A]+[HA]+[A CA [A']+[MA] [M']=M+[MX]+[MX2]+[MX]+[MX4] CM=[M']+[MA] [A],[M]被称为总平衡浓度
如果M与A进行滴定反应,称主反应 M + A MA 将H3A和M同时引入含X的体系,则 cA = [H3A] + [H2A] + [HA] + [A] + [MA] cM = [M] + [MX] + [MX2] + [MX3] + [MX4] + [MA] 将除产物MA以外的平衡浓度的总和记为[A′]和[M′] [A′] = [H3A] + [H2A] + [HA] + [A] cA = [A′] + [MA] [M′] = [M] + [MX] + [MX2] + [MX3] + [MX4] cM = [M′] + [MA] [A′], [M′]被称为总平衡浓度

二、分布系数 浓度为c的HA水溶液,各型体的分布情况 C=[HA]+[A]=[HA]+K,[HA] [H] [H+7 [H] 定义日,A=6为分布系数,即某型体的平衡浓度在分析浓度 CA 中占的分数 [HA] CHA [H四+Ka =[A] Ka CHA[H+K。 结论:G只是H门的函数,知道pH即可求6,[HA=c 求平衡浓度的一种途径
二、分布系数 浓度为 c 的 HA 水溶液,各型体的分布情况 [H ] [H ] ) [HA] [H ] [HA] (1 [H ] [HA] [HA] [A ] [HA] a a - a HA + + + + + = ⋅ + = ⋅ = + = + K K K c 定义 i i c = δ A [H A] 为分布系数,即某型体的平衡浓度在分析浓度 中占的分数 a a HA 0 HA a 1 [H] [A] [H] [HA] [H] K K c c K + = = + = = δ δ 结论:δi只是[H+]的函数,知道 pH 即可求δ,[HiA] = δic 求平衡浓度的一种途径

(例)计算pH=4.0,pH=8.0时0.1mol/LHAc溶液的[HAc], [Ac]. 解:pH=4.0 104 104 6= 10-4+10474 10-35-1007=0.85 6。=0.15 [HAc]=0.085(mol/L),[Ac]=0.015(mol/L) pH=8.0 10-8 10-8+10-479=10-326 60= [HAc]=10426(mol/L),[Ac]=0.1(mol/L)
〈例〉计算 pH = 4.0, pH = 8.0 时 0.1 mol/L HAc 溶液的[HAc], [Ac-]。 解:pH = 4.0 0.15 10 0.85 10 10 10 10 10 0 0.07 3.93 4 4 4.74 4 1 = = = = + = − − − − − − δ δ [HAc] = 0.085 (mol/L), [Ac-] = 0.015 (mol/L) pH = 8.0 1 10 10 10 10 0 3.26 8 4.74 8 1 = = + = − − − − δ δ [HAc] = 10-4.26 (mol/L), [Ac-] = 0.1 (mol/L)
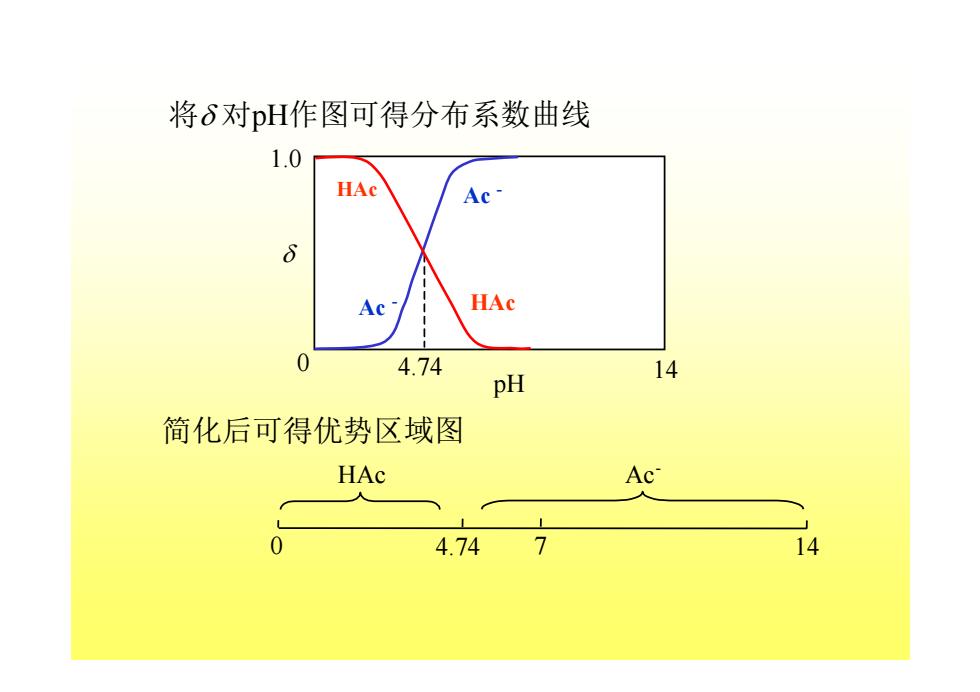
将δ对pH作图可得分布系数曲线 1.0 HAc Ac A HAc 0 4.74 pH 14 简化后可得优势区域图 HAc Ac 0 4.747 14
将δ 对pH作图可得分布系数曲线 简化后可得优势区域图 0 4.74 14 δ pH 1.0 0 4.74 7 14 Ac- HAc HAc Ac - Ac - HAc
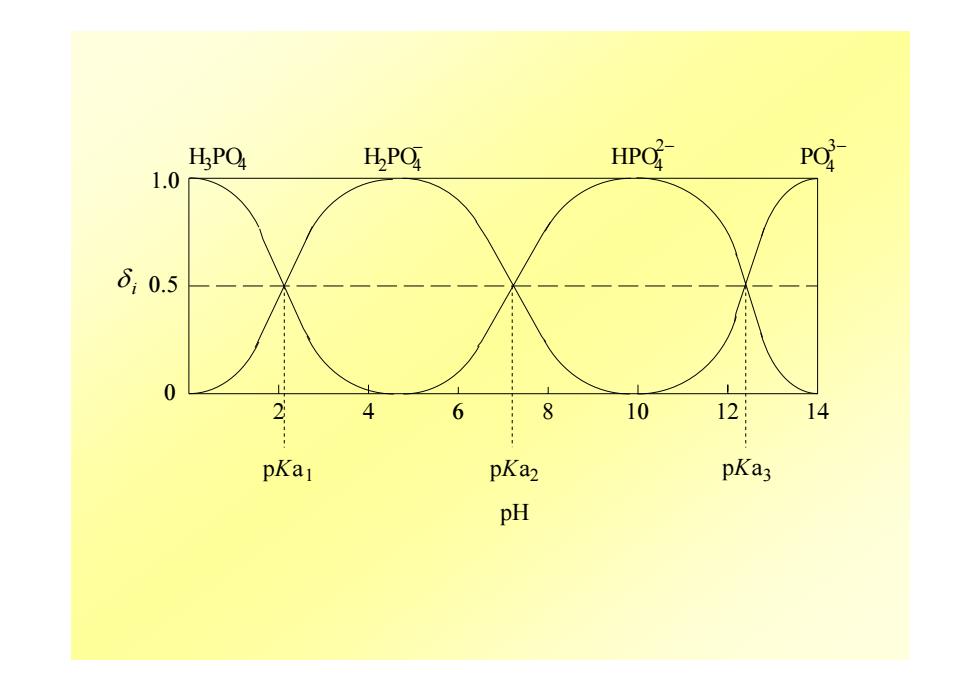
HPQ HPO HPO PO 1.0 60.5 0 2 4 6 8 10 12 14 pKa pKa2 pKa3 pH
0 1.0 2 4 6 8 10 12 14 δ 0.5 H PO H PO HPO PO p i 3 4 2 4 − 1 2 4 2− 4 3− 3 pH Ka pKa pKa
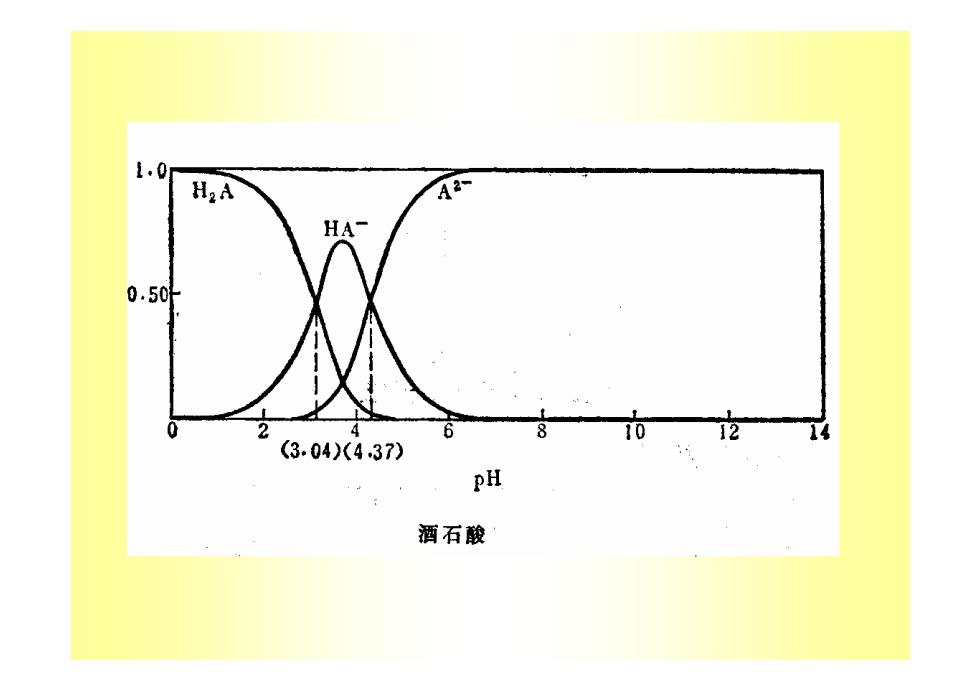
1.0 H2A 42 HA- 0.50叶 0 2 4 6 10 12 (3.04)(437) PH 酒石酸

对于HA =,=1,= Ka Ka Ka 8=1+R™间+面+间 B"[H] 8=1+g+R片间+可 B"[HP ò,=1+B™+B西+可 B[HP 1+B[H]+B[H]2+H] 6,= BH町 ∑P"HI (B= M与X络合 6=LMX」-BX灯 CM ∑B,[X灯T
3 3 2 3 2 1 1 , 1 , 1 H 3 H 2 H 1 K a K a K a K a K a K a 对于 H β = β = β = 3 A H 3 3 H 2 2 H 1 0 1 [ H ] [ H ] [ H ] 1 β β β δ + + + = H 3 3 H 2 2 H 1 H 1 1 1 [ H ] [ H ] [ H ] [ H ] β β β β δ + + + = H 3 3 H 2 2 H 1 H 2 2 2 1 [ H ] [ H ] [ H ] [ H ] β β β β δ + + + = H 3 3 H 2 2 H 1 H 3 3 3 1 [ H ] [ H ] [ H ] [ H ] β β β β δ + + + = ( ) 1 [ H ] [ H ] H H 0 H = = ∑ β β β δ i i i i i M 与 X络合 ∑ = = i i i i i i c [ X ] [MX ] [ X ] M β β δ

(例〉Cd与CN-的配合物,gB1-gB,=5.48,10.60,15.23, 18.78,当[CN=104molL时,求各型体分布系数。 1 解:d=1+AICN]门+B,ICNT+B,ICNT+B.CN丁了 1 =1+105484+1006-3+105232+10876 1 1 1+10+102+10-西+10210西=103 =10148 1034=10-1.6 gs1023 104=10021=0.62 10n=1034=0168=102 gs1026 104=10-06=0.22
〈例〉Cd与CN-的配合物,lgβ1 – lgβ4 = 5.48, 10.60, 15.23, 18.78,当[CN-] = 10-4 mol/L时,求各型体分布系数。 解: - 4 4 - 3 3 - 2 2 - 1 0 1 [CN ] [CN ] [CN ] [CN ] 1 β β β β δ + + + + = 3.44 1.48 2.6 3.23 2.78 3.44 5.48 4 10.6 8 15.23 12 18.78 16 10 10 1 1 10 10 10 10 1 1 10 10 10 10 1 − − − − − = = + + + + = + + + + = 10 0.16 10 10 10 10 10 0.84 3.44 2.6 2 1.96 3.44 1.48 1 = = = = = − − δ δ 10 0.22 10 10 10 0.62 10 10 0.66 3.44 2.78 4 0.21 3.44 3.23 3 = = = = = = − − δ δ