第大章 相平 1873 08 pe 1673 M TIK 熔化物L(单相) 熔化物L(单相) 673 1473 C+L H A+L 1273 A+l 573 E C+L E 1073F N 7B+L A+E C+E C+L B+L C+E B+E8 873 A+C 473 C+E B+E8 0 0.2 0.4C0.6 0.8 1.0 CuCI(A) XFecb FeCl3(B) 0.2 0.4 c06 0.8 10 CaFz(A) CaCl2(B)】 形成稳定化合物的相图 形成不稳定化合物的相图
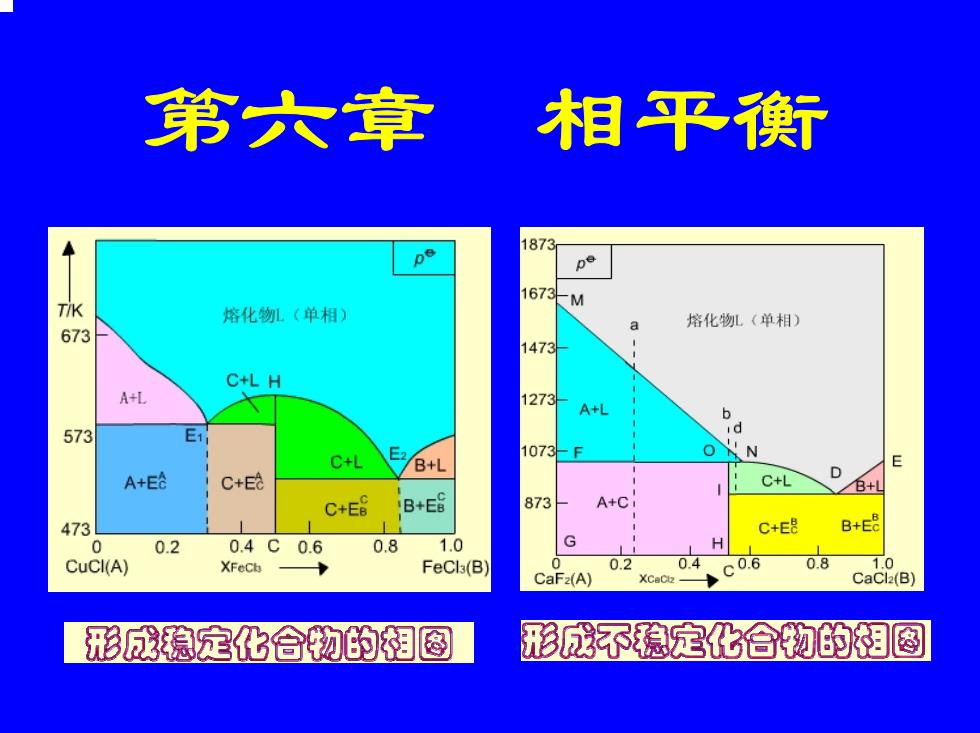
第六章 相平衡

相平衡是热力学在化学领域中的重要应用之一。 研究多相体系的平衡在化学、化工的科研和生产中有 重要的意义,例如:溶解、蒸馏、重结晶、萃取、提 纯及金相分析等方面都要用到相平衡的知识。 研究多相系统的状态随组成、温度、压力等变量 的改变而发生变化,并用图形来表示系统状态的变 化,这种图称为相图(phase diagram)。 相律(phase rule)讨论平衡系统中相数、独立组分 数与描述该平衡系统的变数之间的关系,并揭示了多 相平衡系统中外界条件(温度、压力、组成等)对相变 的关系
相平衡是热力学在化学领域中的重要应用之一。 研究多相体系的平衡在化学、化工的科研和生产中有 重要的意义,例如:溶解、蒸馏、重结晶、萃取、提 纯及金相分析等方面都要用到相平衡的知识。 研究多相系统的状态随组成、温度、压力等变量 的改变而发生变化,并用图形来表示系统状态的变 化,这种图称为相图 (phase diagram) 。 相律 (phase rule ) 讨论平衡系统中相数、独立组分 数与描述该平衡系统的变数之间的关系,并揭示了多 相平衡系统中外界条件 (温度、压力、组成等 )对相变 的关系

6.1相律 6.1.1相数P(number of phase) 系统内部物理性质和化学性质完全均匀的部分 称为相(phase) 气体,不论有多少种气体混合,只有一个气相。 液体,按其互溶程度可以组成一相、两相或三相共存。 固体,一般有一种固体便有一个相。固体溶液除外。 6.1.2组分数C(number of components) ,物种数S(number of substance) 独立的化学反应计量式数目R 不同物种组成间的独立关系数目R' def C-S-R-R
6.1 相律 6.1.1 相数P(number of phase) 系统内部物理性质和化学性质完全均匀的部分 称为相(phase) 气体,不论有多少种气体混合,只有一个气相。 液体,按其互溶程度可以组成一相、两相或三相共存。 固体,一般有一种固体便有一个相。固体溶液除外。 6.1.2 组分数C(number of components) •物种数S(number of substance) •独立的化学反应计量式数目R •不同物种组成间的独立关系数目R’ C = S − R − R′ def

例6.1.1 试确定 H2(g+2(g)=2HI(g) 的平衡系统中,在下述情况下的组分数: (1)反应前只有HⅡ(g); (2)反应前H2(g)及L2(g)两种气体的物质的量相等 (3)反应前有任意量的H(g)及I2(g) 解: C-S-R-R' (1)S=3,R=1;R'=1;C=3-1-1=1 2)S=3,R=1;R'=1;C=3-1-1=1 (3)S=3;R=1;R'=0:C=3-1-0=2
例6.1.1 试确定 H + 2(g) I2(g) 2 HI(g) 的平衡系统中,在下述情况下的组分数: (1)反应前只有HI(g); (2)反应前H2(g)及I2 (g)两种气体的物质的量相等; (3)反应前有任意量的H2(g)及I2 (g). 解: C = S - R - R’ (1) S = 3; R =1; R’ =1; C = 3 -1 -1 =1 (2) S = 3; R =1; R’ =1; C = 3 -1 -1 =1 (3) S = 3; R =1; R’ =0; C = 3 -1 -0 =2

例6.1.2试求下述系统中的组分数: (①)由任意量的有CaCO,(s)、CaO(s)、CO,(g)反应达 到平衡的系统; (ii)仅由CaCO,(s)部分分解达到平衡的系统! 解: C-S-R-R' (1)S=3;R=1;R'=0;C=3-1-0=2 (2)S=3;R=1;R'=0;C=3-1-0=2
例6.1.2 试求下述系统中的组分数: (i)由任意量的有CaCO3(s)、CaO(s)、CO2(g)反应达 到平衡的系统; (ii) 仅由CaCO3(s)部分分解达到平衡的系统. 解: C = S - R - R’ (1) S = 3; R =1; R’ =0; C = 3 -1 -0 =2 (2) S = 3; R =1; R’ =0; C = 3 -1 -0 =2

6.1.3自由度数F(number of degree of freedom) 在不改变系统中原有平衡相数的条件下,确定 系统的平衡状态所需的独立强度变量(温度、压力、 组成等)称为系统的自由度(degree offreedom),这种 变量的数目称为自由度数,用符号F表示。 6.1.4 吉布斯相律(Gibbs'phase rule) F=C-P+2 条件自由度数F’: F’=C一P+1 F=C一P+b 证明
6.1.3 自由度数 F (number of degree of freedom) 在不改变系统中原有平衡相数的条件下,确定 系统的平衡状态所需的独立强度变量(温度、压力、 组成等)称为系统的自由度(degree of freedom),这种 变量的数目称为自由度数,用符号F表示。 6.1.4 吉布斯相律(Gibbs’ phase rule) F= C-P+ 2 条件自由度数 F’ : F’ = C- P + 1 F = C- P + b 证明

吉布斯相律的证明: 设有一个多相平衡系统包含S种物质,分布在P个相中。 例如a相,温度Ta、压力p和各组分的组成x、x、 xS1,共有(S-1)+2=S+1个强度性质。 此平衡系统中共有P个相,描述平衡系统的总变量数为 P(S+1)
吉布斯相律的证明: 设有一个多相平衡系统包含S 种物质,分布在P个相中。 例如α 相,温度Tα、压力pα和各组分的组成 、 、 . ,共有(S—1)+2=S+1个强度性质。 α 1 x α2 x α S−1 x 此平衡系统中共有P个相,描述平衡系统的总变量数为 P(S+1)

热力学平衡状态必须满足下列平衡条件: ①热平衡条件:T1=TP=.=TP, 共有(P-1)个 (2)力学平衡条件:pl=p2==pP, 共有(P1)个 (3)相平衡条件: =4== =.=2 ==.=S ,共有S(P-1)个 (4)化学平衡条件:独立的化学反应计量式数目R, R'个独立组成关系数目
热力学平衡状态必须满足下列平衡条件: (l)热平衡条件: T1 = T2 = . = TP , 共 有 ( P-1) 个 (2)力学平衡条件: p 1 = p 2 = . = p P, 共 有 (P-1) 个 (3)相平衡条件: P 1 2 1 1 1 µ = µ = L = µ P 2 2 2 1 2 µ = µ = L = µ P S 2 S 1 S µ = µ = L = µ ........... ,共有 S (P-1) 个 (4)化学平衡条件:独立的化学反应计量式数目 R , R’个独立组成关系数目

2(P-1)+S(P-I)+R+R =(P-1)S+2)+R+R F=平衡系统的总变量数一平衡时变量间 必须满足的关系式的数目 F={S+1)}一{(P1)S+2)+R+R'} =(S-R-R)-P+2 F=C-P十2 返回
2(P—1)+S(P—l)+R+R’ =(P—1)(S+2)+R+R’ F = 平衡系统的总变量数 - 平衡时变量间 必须满足的关系式的数目 F ={P(S+1)}-{(P—1)(S+2)+R+R’} =(S-R-R’)-P+2 F =C-P+2 返回

例6.1.3试计算下述平衡系统中的自由度数F: (①)由C02(s)及C02(g)建立的平衡系统, (i)由HgO(s)分解为Hg(g)及O,(g)建立的平衡系统, 解: C-S-R-R F=C-P+2 (1)S=1;R=0,R'=0,C=1-0-0=1 P=2;F=1-2+2=1 2)S=3;R=1;R'=1;C=3-1-1=1 P=2,F=1-2+2=1
例6.1.3 试计算下述平衡系统中的自由度数F : (i)由CO2(s)及CO2(g)建立的平衡系统; (ii)由HgO(s)分解为Hg(g)及O2(g)建立的平衡系统. 解: C = S - R - R’ F=C-P+2 (1) S = 1; R =0; R’ =0; C = 1 -0 -0 =1 P=2; F = 1 -2 +2 =1 (2) S = 3; R =1; R’ =1; C = 3 -1 -1 =1 P =2; F = 1 -2 +2 =1