
非线性物理:混沌物理 混沌的几何特征: 通过前面的一系列具体实例、李雅普洛夫指数和吸引子形态的分 析,我们明白非线性系统的演化来自于驱动、耗散和非线性的共 同作用。 ·驱动使系统离开原来状态,耗散保持系统整体结构,非线性使系 统具有几何与拓扑上的多样性。 ·从几何学上理解混沌结构是有价值的。 从简单例子开始:
非线性物理:混沌物理 混沌的几何特征: • 通过前面的一系列具体实例、李雅普洛夫指数和吸引子形态的分 析,我们明白非线性系统的演化来自于驱动、耗散和非线性的共 同作用。 • 驱动使系统离开原来状态,耗散保持系统整体结构,非线性使系 统具有几何与拓扑上的多样性。 • 从几何学上理解混沌结构是有价值的。 • 从简单例子开始:

非线性物理:混沌物理 2xn,0≤xn≤1/2 帐篷映射:Xn+1=T(xn)= 2-2xn,1/2<xn≤1 2xn,0≤xn<1/2 锯齿映:Xn+1=S(Xn)= 2xn-1,1/2≤xn≤1 这两类映射具有局域演变的两个特点:伸长与折叠。 帐篷映射第一半是驱动过程,具有伸长性质;后一半是耗散反馈 过程,将伸长又折叠回来。构成局域的分叉甚至是混沌。 ·几何示意图如下:
非线性物理:混沌物理 • 帐篷映射: • 锯齿映射: • 这两类映射具有局域演变的两个特点:伸长与折叠。 • 帐篷映射第一半是驱动过程,具有伸长性质;后一半是耗散反馈 过程,将伸长又折叠回来。构成局域的分叉甚至是混沌。 • 几何示意图如下:

非线性物理:混沌物理 伸长 折叠 2xn,0≤xn≤1/2 xn+1=T(xn)= 2-2xn,1/2<xn≤1 ·锯齿映射显得更为有趣:将x看成角变量,映射是圆上的映射, x从0到1对应于旋转一周,映射前一半是圆周伸长一倍,后一 半将圆周扭转成8字型,再折叠成近似重合的一个圆:
非线性物理:混沌物理 • 锯齿映射显得更为有趣:将 x 看成角变量,映射是圆上的映射, x 从 0 到 1 对应于旋转一周,映射前一半是圆周伸长一倍,后一 半将圆周扭转成 8 字型,再折叠成近似重合的一个圆:
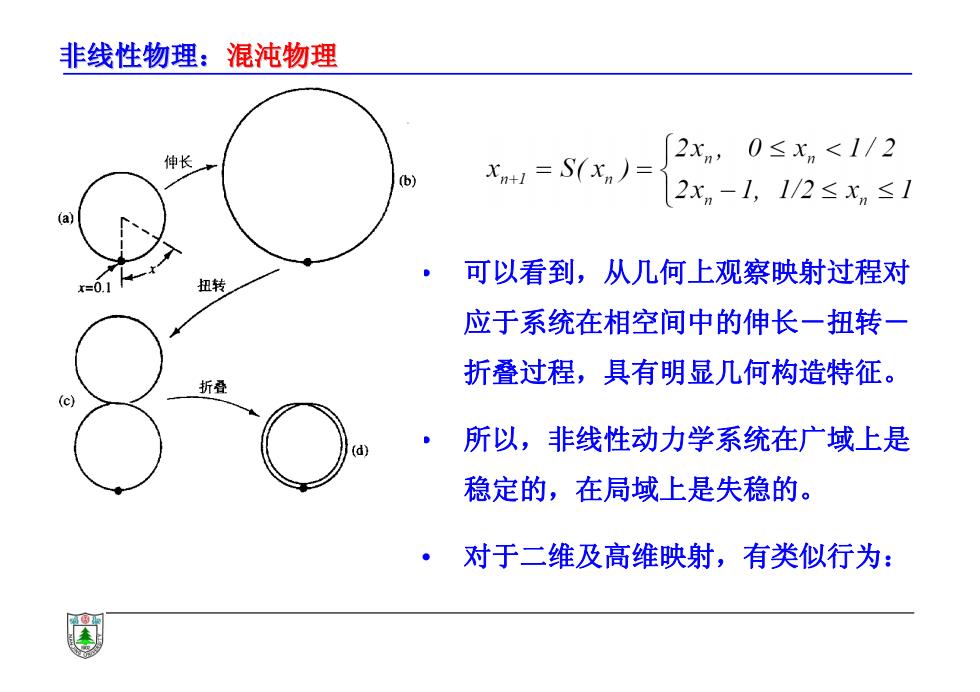
非线性物理:混沌物理 伸长 (6) x1=S(xn)= 2xn,0≤x,<1/2 2xn-1,1/2≤xn≤1 a 扭转 可以看到,从几何上观察映射过程对 应于系统在相空间中的伸长一扭转一 折叠过程,具有明显几何构造特征。 析叠 (c) (d) ·所以,非线性动力学系统在广域上是 稳定的,在局域上是失稳的。 ·对于二维及高维映射,有类似行为:
非线性物理:混沌物理 • 可以看到,从几何上观察映射过程对 应于系统在相空间中的伸长-扭转- 折叠过程,具有明显几何构造特征。 • 所以,非线性动力学系统在广域上是 稳定的,在局域上是失稳的。 • 对于二维及高维映射,有类似行为:
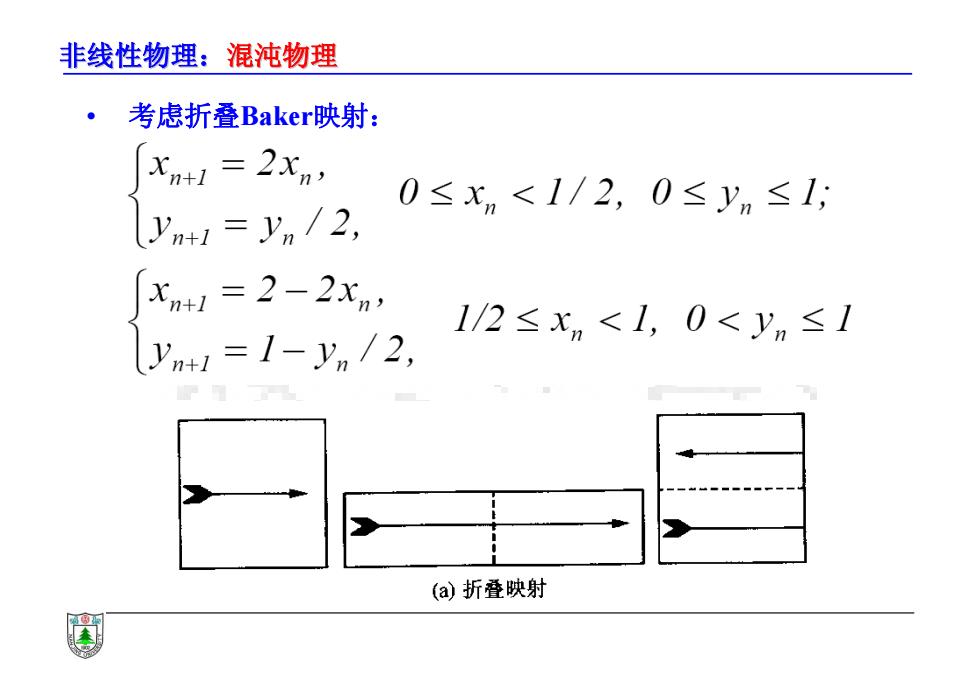
非线性物理:混沌物理 ·考虑折叠Baker映射: Xn+l=2Xn, 0≤xn<1/2,0≤yn≤1, n yn/2, Xn1=2-2xn, 1/2≤xm<1,0<yn≤1 yn+1=1-yn/2, (a)折叠映射
非线性物理:混沌物理 • 考虑折叠Baker映射:
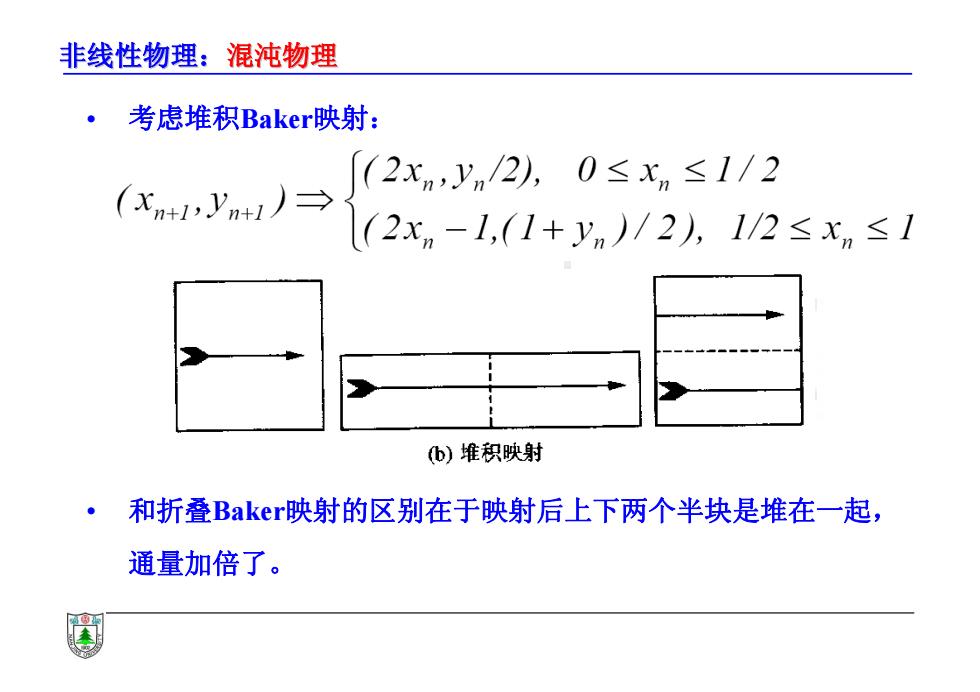
非线性物理:混沌物理 考虑堆积Bakerl映射: (2xn,yn/2),0≤xn≤1/2 (X+1yn+1)→ (2xm-1,(1+yn)/2,1/2≤xn≤1 b)堆积映射 ·和折叠BakerF映射的区别在于映射后上下两个半块是堆在一起, 通量加倍了
非线性物理:混沌物理 • 考虑堆积Baker映射: • 和折叠Baker映射的区别在于映射后上下两个半块是堆在一起, 通量加倍了

非线性物理:混沌物理 · 再看Small马蹄映射: (xn+1,yn+1)→ J(xn/3,3yn),0≤yn≤1/3 (1-xn/3,3(1-yn月,2/3≤yn≤1 。 这一过程通过伸 E 长和折叠变成了 D E 一个马蹄。 D B D (a) B A (b) (c)
非线性物理:混沌物理 • 再看Small马蹄映射: • 这一过程通过伸 长和折叠变成了 一个马蹄

非线性物理:混沌物理 ·除了伸长、折叠、扭转之外,还有剪切过程存在,一般发生在三 维情况下:(x1,yn+1,之1)→ (2xn,yn/2,f0yn/2八,0≤xn<1/2 (2-2xn,1-yn/2,f1-yn/2月,1/2≤yn≤1 f(y)=y-1/2 先是伸长,然后扭转,再是剪切。 非线性系统演化是伸长、折叠、扭转、剪切 ,传统线性动力学只是岿然不动或者原地兜 圈。 图2.8伸长一折叠一剪切映射
非线性物理:混沌物理 • 除了伸长、折叠、扭转之外,还有剪切过程存在,一般发生在三 维情况下: • 先是伸长,然后扭转,再是剪切。 • 非线性系统演化是伸长、折叠、扭转、剪切 ,传统线性动力学只是岿然不动或者原地兜 圈

非线性物理:混沌物理 局域失稳导致分形特征: 从上述几何特征看出混沌系统首先要求局域失稳和广义稳定。先 讨论广域稳定的边界几何特征。 ·非线性混沌动力学系统的奇异吸引子实际上就是其广域稳定性的 表现。很多情况下,这类广域边界是分形结构。 从最经典的Julia和Mandelbroti迭代映射开始讨论问题。 。 Julia集取名于法国数学家Gaston Julia,他在1915年开始研究简 单复平面的迭代问题,在1918年发表一篇著名论文。当时他研究 的是一个复杂的多项式:z+(?-)+z23+4z2+5)+c
非线性物理:混沌物理 局域失稳导致分形特征: • 从上述几何特征看出混沌系统首先要求局域失稳和广义稳定。先 讨论广域稳定的边界几何特征。 • 非线性混沌动力学系统的奇异吸引子实际上就是其广域稳定性的 表现。很多情况下,这类广域边界是分形结构。 • 从最经典的Julia和Mandelbrot迭代映射开始讨论问题。 • Julia集取名于法国数学家Gaston Julia,他在1915年开始研究简 单复平面的迭代问题,在1918年发表一篇著名论文。当时他研究 的是一个复杂的多项式:z4 + z3/(z-1) + z2/(z3 + 4 z2 + 5) + c

非线性物理:混沌物理 我们研究的Julia迭代要简单些:一个复平面,x+。考虑迭代 乙+1F12+c,其中c为一个复常数,是复平面上每一点。 ·迭代的图形变化由c的值决定。 从更一般角度看,Julia集:乙n+f亿,,这里f为非线性函数。 通常使用的Julia函数包括:n+=Csin(亿,n+=C∝p(亿 zn+CiC0s(亿,zn+=czn(I-zd。 我们现在来考虑最著名的Juia集如何计算:z+厂乙n2+c
非线性物理:混沌物理 • 我们研究的Julia迭代要简单些:一个复平面,z=x+iy。考虑迭代 zn+1= zn2+c,其中c为一个复常数,z0是复平面上每一点。 • 迭代的图形变化由 c 的值决定。 • 从更一般角度看,Julia集:zn+1=f(zn),这里f(z)为非线性函数。 • 通常使用的Julia函数包括:zn+1=c sin(zn), zn+1=c exp(zn), zn+1=c i cos(zn), zn+1=c zn(1-zn)。 • 我们现在来考虑最著名的Julia集如何计算: zn+1=zn2+c