
非线性物理:分形物理 特征尺度问题: 物理学家关注自然现象中的特征尺度,然后寻找数学描述方法! 关注有序无序! 自然界的构造动力模式:规则和完全随机之间的! 规则构成导致所谓周期排列或者准周期排列,例如晶体、社会组 织、军队方阵等等,都有特征尺度。从形成动力学看,是近平衡 生长或者组织形成的。 自然界随机过程和现象更加广泛:没有特征尺度!
非线性物理:分形物理 特征尺度问题: • 物理学家关注自然现象中的特征尺度,然后寻找数学描述方法! 关注有序无序! • 自然界的构造动力模式:规则和完全随机之间的! • 规则构成导致所谓周期排列或者准周期排列,例如晶体、社会组 织、军队方阵等等,都有特征尺度。从形成动力学看,是近平衡 生长或者组织形成的。 • 自然界随机过程和现象更加广泛:没有特征尺度!

非线性物理:分形物理
非线性物理:分形物理
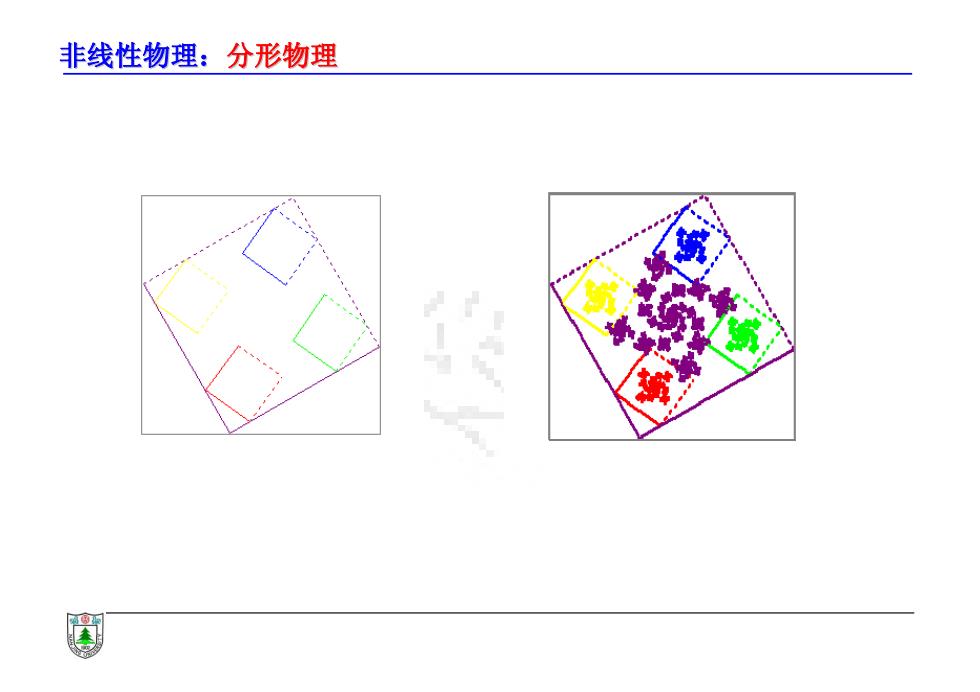
非线性物理:分形物理
非线性物理:分形物理

非线性物理:分形物理 (0,0.16yn 0.00<r<0.01 0.2xn-0.26yn,0.23xn+0.22yn+0.2), 0.01<r<0.08 (x+yn+1)= -0.15xn+0.28yn,0.26xn+0.24yn+0.2,0.08<r<0.15 0.85xn+0.04yn,-0.04xn+0.85yn+0.2,0.15<r<1.00
非线性物理:分形物理 (0.85x 0.04y ,-0.04x 0.85y 0.2), 0.15 r 1.00 (-0.15x 0.28y ,0.26x 0.24y 0.2), 0.08 r 0.15 (0.2x -0.26y ,0.23x 0.22y 0.2), 0.01 r 0.08 (0,0.16 y ), 0.00 r 0.01 ( x , y ) n n n n n n n n n n n n n n 1 n 1

非线性物理:分形物理 分形维: 这类没有特征尺度的物体成为分形体。既然没有特征尺度,如何 去描述它的几何特征?以Koch曲线为例: ·对单位长度线段,无论用何种尺度δ去测量,其长度L均为1: L=60=1
非线性物理:分形物理 分形维: • 这类没有特征尺度的物体成为分形体。既然没有特征尺度,如何 去描述它的几何特征?以Koch曲线为例: • 对单位长度线段,无论用何种尺度 去测量,其长度 L 均为1: L 1 0

非线性物理:分形物理 用6=13尺度测量,小于6的弯曲部分被遗弃,L(6=1/3)=4/3; 依此类推: -(g引 -N.8 根据维度定义,应该有:L=6=N6,这里是余数维。因此, (4/3)"=(1/3)"u=N6,所以有:μE=1-ln4n3=-0.2618,定义=1-D月 ,有Dn4/n3=1.2618,称为Hausdorff分形维。 N=δ-DH Da=lnN/lnδ-)
非线性物理:分形物理 • 用 =1/3 尺度测量,小于 的弯曲部分被遗弃,L( =1/3)=4/3; 依此类推: • 根据维度定义,应该有:L= =N ,这里是余数维。因此, (4/3)n=(1/3)n =N ,所以有: =1-ln4/ln3=-0.2618,定义=1-DH ,有DH=ln4/ln3=1.2618,称为Hausdorff分形维。 N 34 31 L n n D ln N /(ln ) N 1 H DH

非线性物理:分形物理 ·对一个正方体:N~62,所以D=2.0。对于一个立方体:N~63, 所以DH3.0。 ·如图所示的Sierpinski?三角形,映射到 第n步,δ=(1/2)=2",而相应的面积 单元数目N=3"。所以,维度DH为: N~δDH三3n~2mDH→nln3=nDu In2 Du In3/In 2
非线性物理:分形物理 • 对一个正方体:N~ 2,所以DH=2.0。对于一个立方体: N~ 3, 所以DH=3.0。 • 如图所示的Sierpinski三角形,映射到 第n步, =(1/2)n=2-n,而相应的面积 单元数目N=3n。所以,维度DH为: D ln 3 / ln 2 N ~ 3 ~ 2 nln 3 nD ln 2 H H DH n n DH
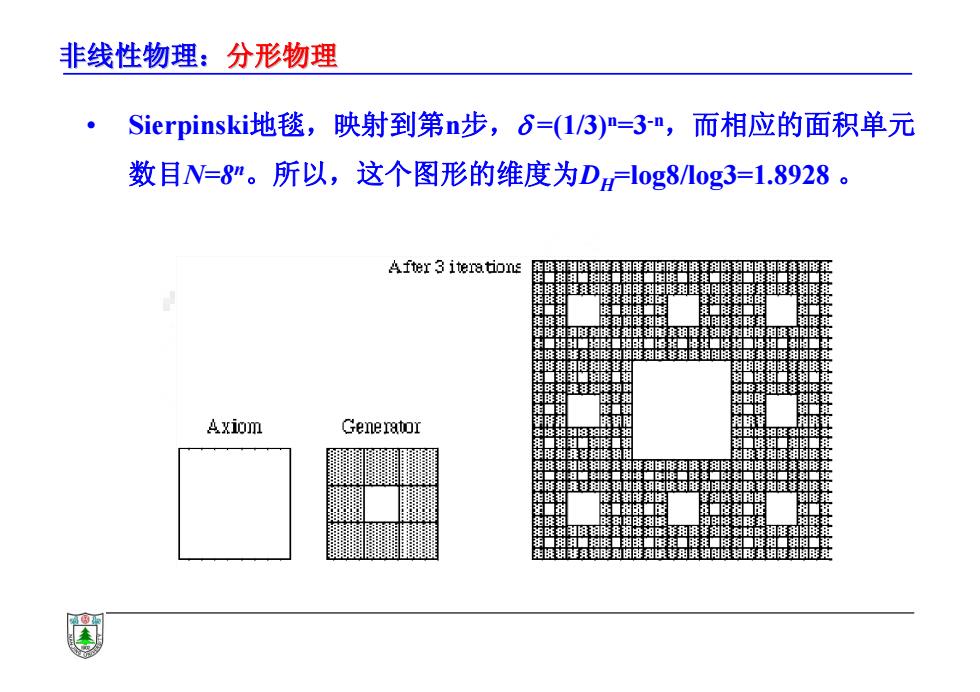
非线性物理:分形物理 Sierpinski地毯,映射到第n步,6=(1/3)=3-",而相应的面积单元 数目N=8"。所以,这个图形的维度为D=log81og3=1.8928。 After 3 iterations Axiom Gene rator
非线性物理:分形物理 • Sierpinski地毯,映射到第n步, =(1/3)n=3-n,而相应的面积单元 数目N=8n。所以,这个图形的维度为DH=log8/log3=1.8928

非线性物理:分形物理 天线发射
非线性物理:分形物理 天线发射
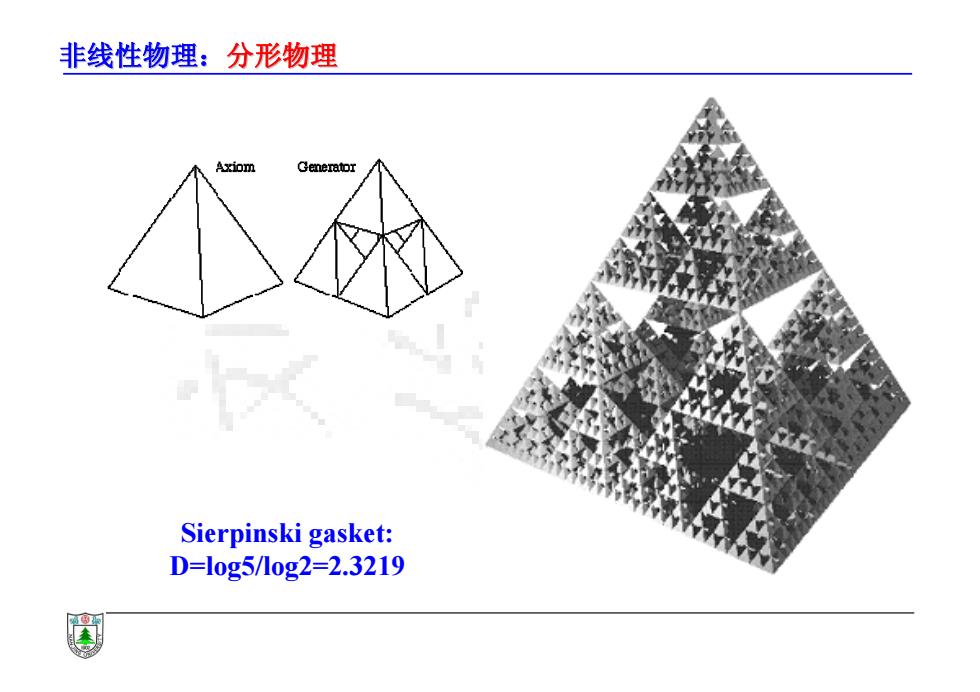
非线性物理:分形物理 Axiom Generator Sierpinski gasket: D=l0g5/1og2=2.3219
非线性物理:分形物理 Sierpinski gasket: D=log5/log2=2.3219