
第20章光的干涉和衍射 §20.1光波的相干叠加 §20.2双缝千涉 §20.3薄膜干涉 §20.4偏振光的干涉 §20.5光的衍射 §20.6光栅衍射 §20.7圆孔衍射光学仪器的分辨本领 §20.8X射线的衍射
§20.1 光波的相干叠加 §20.3 薄膜干涉 §20.4 偏振光的干涉 §20.5 光的衍射 §20.6 光栅衍射 §20.7 圆孔衍射 光学仪器的分辨本领 §20.8 X射线的衍射 第 20 章 光的干涉和衍射 §20.2 双缝干涉
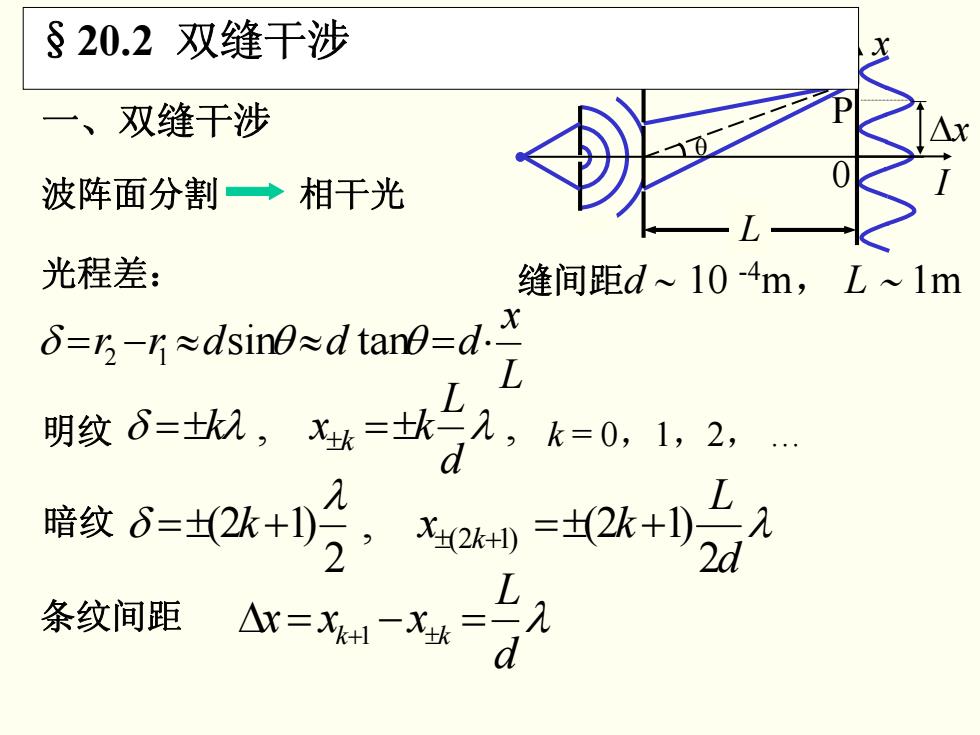
§20.2双缝干涉 一、双缝干涉 波阵面分割→相干光 光程差: 缝间距d~104m,L~1m δ=3-r≈dsin0≈d tan0=d.x 明纹6=士九,Xk=士比九,k=0,1,2, 暗纹6=2k+0,2=2k+022 条纹间距 --2
一、双缝干涉 Δx 缝间距d ∼ 10 光程差: -4m, L ∼ 1m L x δ 12 tansin θθ dddrr ⋅=≈≈−= 明纹 λδ , λ , dLkxk ±k ±=±= 暗纹 2 , )1 2( 2)1 2( )12( λ λ δ dL kxk +±= k+± +±= 波阵面分割 相干光 k = 0,1,2, … 条纹间距 λ d L xxx 1 ±+ kk =−=Δ L x 0 I P θ §20.2 双缝干涉
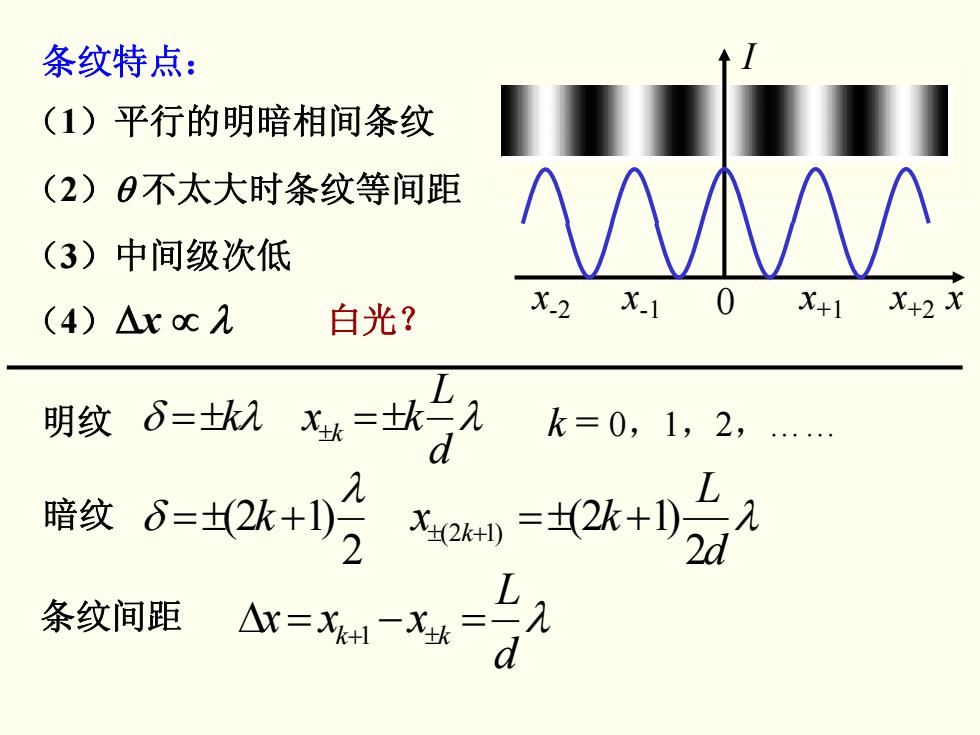
条纹特点: (1)平行的明暗相间条纹 (2)0不太大时条纹等间距 (3)中间级次低 AΛΛ (4)△xc2 白光? X-2 X.1 X+1 X+2X 明纹6=士x*=比二入 k=0,1,2,… 陪纹-2k+=2k+始A 条纹间距 Ax=-x=入
M (1)平行的明暗相间条纹 (3)中间级次低 (4)Δx ∝ λ 条纹特点: (2)θ 不太大时条纹等间距 x I 0 x+1 x+2 x-1 x 白光? -2 明纹 λδ λdLkxk ±k ±=±= 暗纹 2)1 2( 2)1 2( )12( λ λ δ dL kxk +±= k+± +±= k = 0,1,2,…… 条纹间距 λ d L xxx 1 ±+ kk =−=Δ
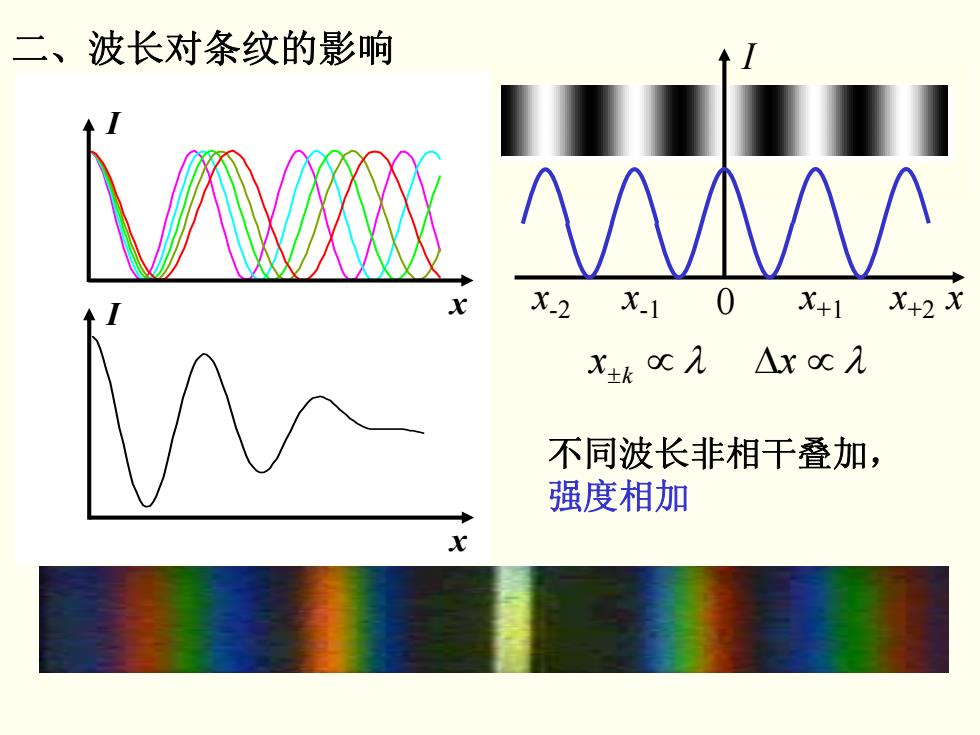
二、波长对条纹的影响 A个小△ X-2 X1 0 X+1 X+2X X士kC ,△xc入 不同波长非相干叠加, 强度相加
M 1.8 1.5 y1i y2i y3i y4i y5i 0 x 31.415927 i I x x I 0 x+1 x+2 x-1 x-2 不同波长非相干叠加, 强度相加 x±k x ∝Δ∝ λλ 4.917482 4.71839 y i 0 x 31.415927 i I x 二、波长对条纹的影响
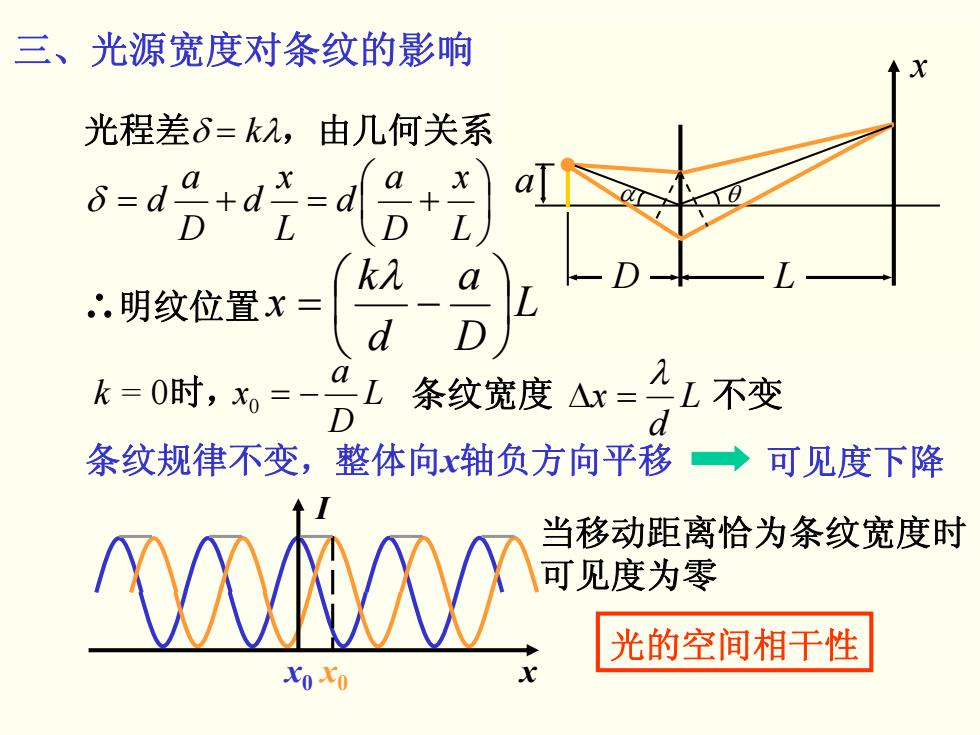
三、光源宽度对条纹的影响 光程差6=k几,由几何关系 k入 ∴.明纹位置x= d k=0时,0=- 条纹宽度r=2L不变 d 条纹规律不变,整体向x轴负方向平移 ◆ 可见度下降 Vǜ 当移动距离恰为条纹宽度时 可见度为零 光的空间相干性
D L θ a α 三、光源宽度对条纹的影响 x ⎟⎠⎞ ⎜⎝⎛ +=+= Lx Da d Lx d Da δ d 光程差δ = kλ,由几何关系 L D a d k x ⎟⎠⎞ ⎜⎝⎛ −= λ ∴明纹位置 k = 0时, L D a x0 −= L d x λ 条纹宽度 =Δ 不变 条纹规律不变,整体向x轴负方向平移 x I x0 x0 可见度下降 当移动距离恰为条纹宽度时 可见度为零 光的空间相干性
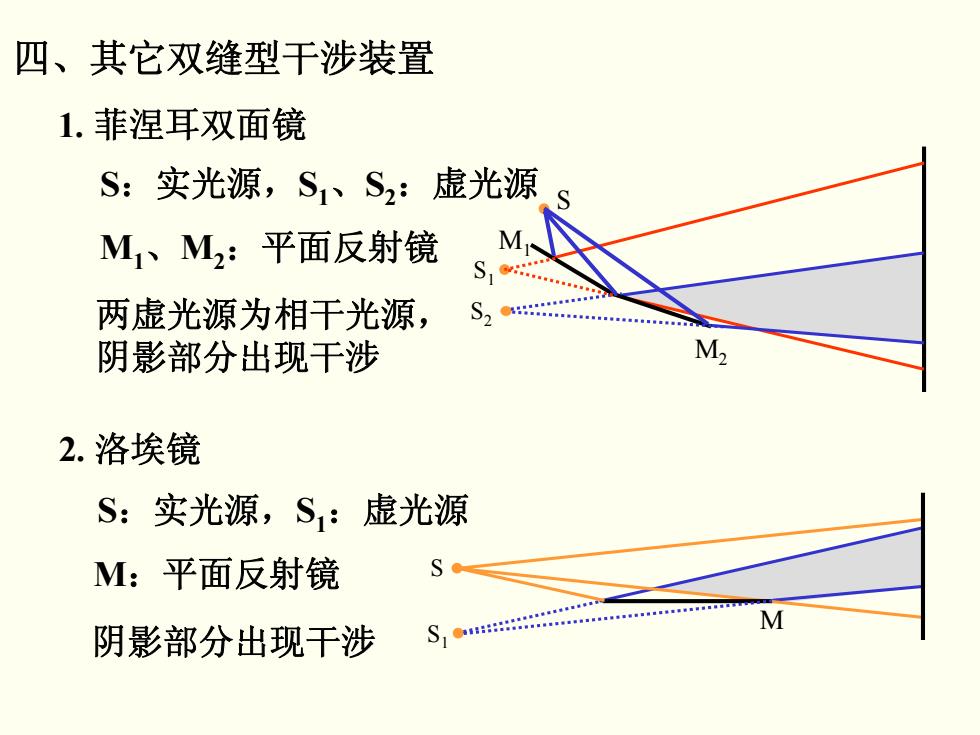
四、其它双缝型干涉装置 1.菲涅耳双面镜 S:实光源,S1、S2:虚光源 M1、M,:平面反射镜 M S 两虚光源为相干光源, S2。 阴影部分出现干涉 M 2.洛埃镜 S:实光源,S:虚光源 M:平面反射镜 阴影部分出现干涉 S1●
四、其它双缝型干涉装置 1. 菲涅耳双面镜 2. 洛埃镜 S:实光源, S 1 、 S 2:虚光源 M 1 、 M 2:平面反射镜 两虚光源为相干光源, 阴影部分出现干涉 S:实光源, S 1:虚光源 M:平面反射镜 阴影部分出现干涉 S S1 S 2 M1 M 2 S1 S M
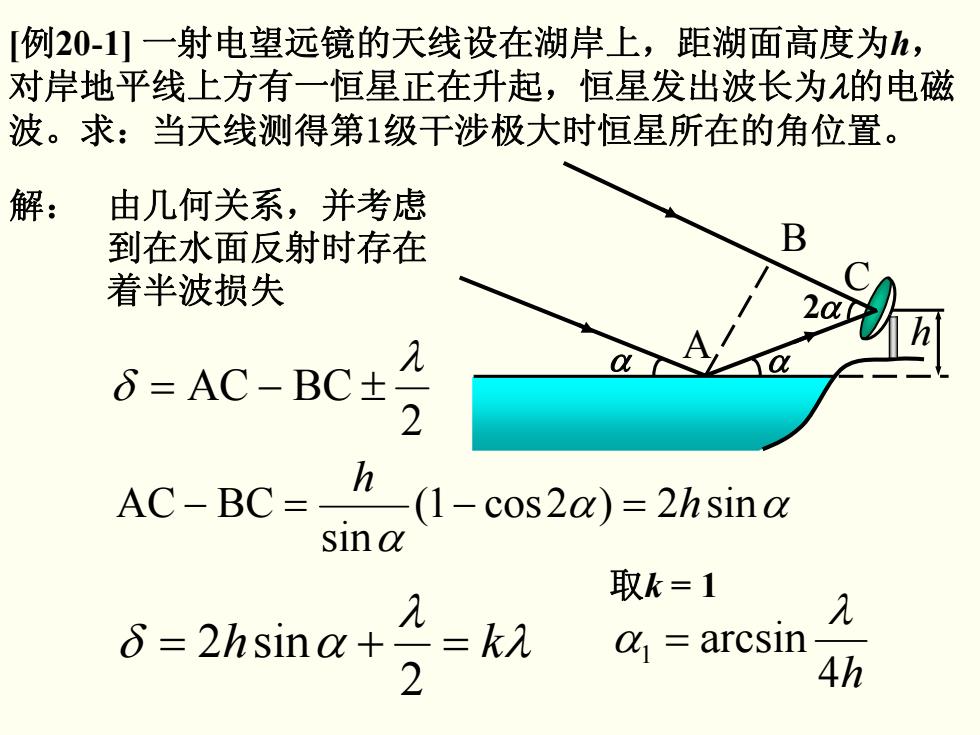
[例20-1]一射电望远镜的天线设在湖岸上,距湖面高度为, 对岸地平线上方有一恒星正在升起,恒星发出波长为2的电磁 波。求:当天线测得第1级干涉极大时恒星所在的角位置。 解: 由几何关系,并考虑 到在水面反射时存在 着半波损失 δ=AC-BC± 2 AC-BC= h (1-cos2a)=2hsina sina 取k=1 δ=2 hsina+ =k a arcsin 2 4h
[例20-1] 一射电望远镜的天线设在湖岸上,距湖面高度为h, 对岸地平线上方有一恒星正在升起,恒星发出波长为λ的电磁 波。求:当天线测得第1级干涉极大时恒星所在的角位置。 2 BCAC λ δ ±−= α α α sin2)2cos1( sin BCAC h h =−=− λ λ h αδ =+= k 2 sin2 4h 1 arcsin λ α = 解: h C A B α α 2α 由几何关系,并考虑 到在水面反射时存在 着半波损失 取k = 1

[例20-2]用薄云母片(=1.58)覆盖在杨氏双缝的中一条缝 上,这时屏上的零级明纹移到原来的第七级明纹处。如果入 射光波长为550nm,问云母片的厚度为多少? 解:原七级明纹P点处 3-飞=7九 插入云母后,P点为零级明纹 ⊙2 3-(G-d+nd)=0 7=d(n-1) d=_ 元7×550×109 =6.6×10-6m n-1 1.58-1
[例20-2] 用薄云母片(n=1.58)覆盖在杨氏双缝的中一条缝 上,这时屏上的零级明纹移到原来的第七级明纹处。如果入 射光波长为550nm,问云母片的厚度为多少? 解:原七级明纹P点处 rr 12 =− 7λ 插入云母后,P点为零级明纹 ( ) 12 −− + nddrr = 0 λ = (nd −17 ) m106.6 158.1 105507 1 7 6 9 − − ×= − ×× = − = n d λ P 0 d S1 S2 r1 r2

[例20-3]杨氏双缝的间距为0.2mm,距离屏幕为1m。 (1)若第一到第四明纹距离为7.5mm,求入射光波长。 (2)若入射光的波长为600nm,求相邻两明纹的间距。 解:x=士上k入 (k=0,1,2,…) d △x1,4= 4-¥=之民,k归 d A4_0.2×1037.5×103 =5×10m -k 1 4-1 L 1×6×10-7 △x d 0.2x109-3×10-3m-3mm END
[例20-3] 杨氏双缝的间距为0.2mm,距离屏幕为1m。 (1)若第一到第四明纹距离为7.5mm,求入射光波长。 (2)若入射光的波长为600nm,求相邻两明纹的间距。 ±= ( ) kk = ,2,1,0 L dL x λ 144,1 ( ) kk 14 λ dL xxx −=−=Δ m105 14 105.7 1 102.0 7 3 3 14 4,1 − − − ×= − ×× = − Δ ⋅= kk x L d λ mm3m103 102.0 1061 3 3 7 =×= × ×× ==Δ − − − λ d L x 解: END