
第16章变化的电兹场 §16.1电磁感应定律 §16.2动生电动势 §16.3感生电动势 感应电场 §16.4自感和互感 §16.5电容和电感电路中的暂态电流 §16.6磁场能量 §16.7位移电流 §16.8麦克斯韦电磁场方程组
第 16 章 变化的电磁场 §16.2 动生电动势 §16.1 电磁感应定律 §16.3 感生电动势 感应电场 §16.4 自感和互感 §16.6 磁场能量 §16.7 位移电流 §16.8 麦克斯韦电磁场方程组 §16.5 电容和电感电路中的暂态电流
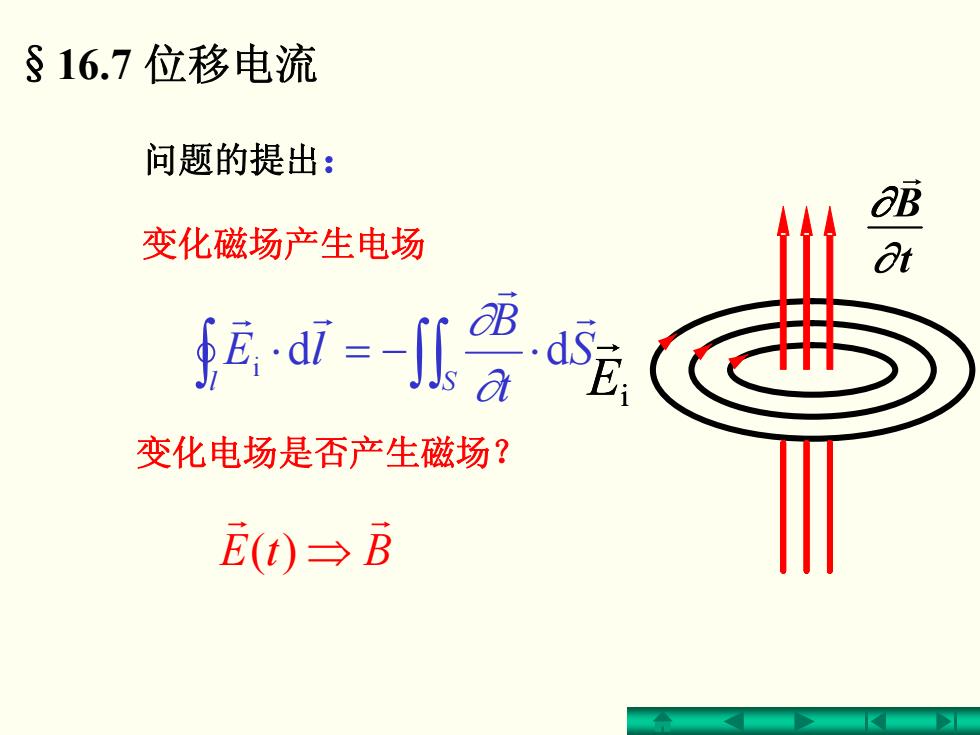
§16.7位移电流 问题的提出: ∂B 变化磁场产生电场 t fd-小酒 变化电场是否产生磁场? E(t)三B
§16.7 位移电流 问题的提出: ∫∫∫ ⋅−=⋅ l S S tB lE r r r r d d i ∂ ∂ BtE r r )( ⇒ 变化磁场产生电场 变化电场是否产生磁场?

一、位移电流假设 对于稳恒电流 fidi=1.=八元.d fadi=? fidi=八元ds=1。 1.5 fidi=八元ds=0 非稳恒电流
一、位移电流假设 对于稳恒电流 ∫∫∫ ⋅==⋅ l S SjIlHr r r r d d c c c c 1 d d ISjlH l S =⋅=⋅ ∫∫∫ r r r r d 0d 2 c =⋅=⋅ l ∫∫∫ S SjlHr r r r =⋅ ?d ∫l lHr r 非稳恒电流
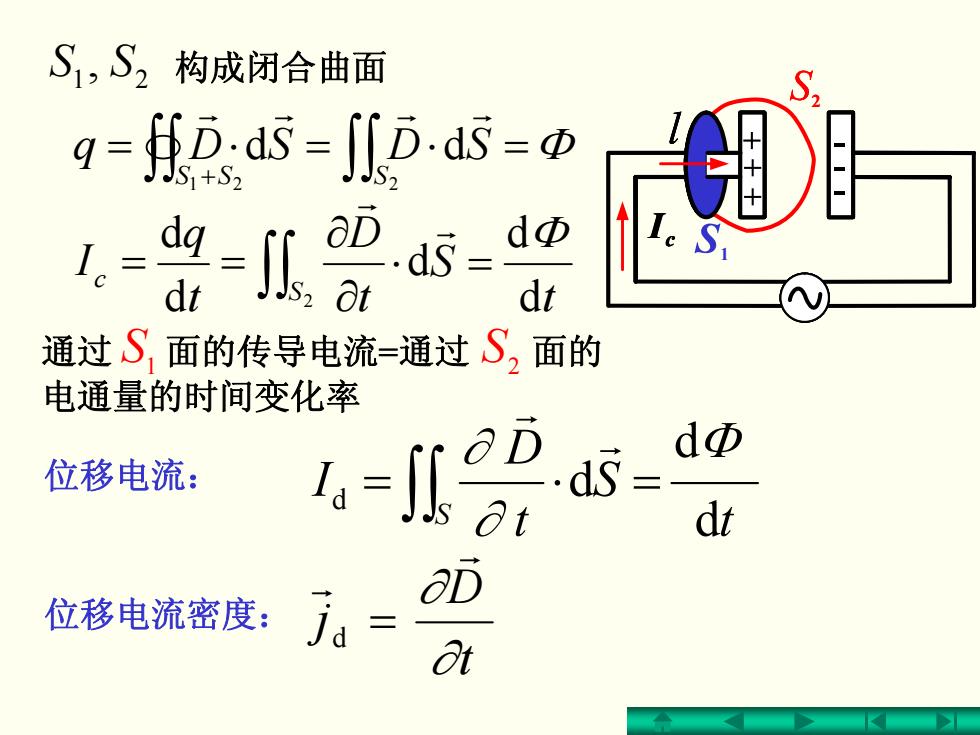
S1,S2构成闭合曲面 g=fDa-川Dds=p 1的-9s Ie S dt 通过S,面的传导电流=通过S,面的 电通量的时间变化率 dΦ 位移电流: dt 位移电流密度:j:= D a
t S t D t q I S c d d d d d 2 Φ =⋅ ∂ ∂ == ∫∫ r r t S t D I S d d d d Φ ∂ ∂ =⋅= ∫∫ r r t D j ∂ ∂ r r 位移电流密度: d = ∫∫∫∫ =⋅=⋅= Φ + 21 2 dd SS S SDSDq r r r r 通过 面的传导电流 =通过 面的 电通量的时间变化率 1 S 2 S 位移电流: , S 1 S 2 构成闭合曲面 1 2 c I
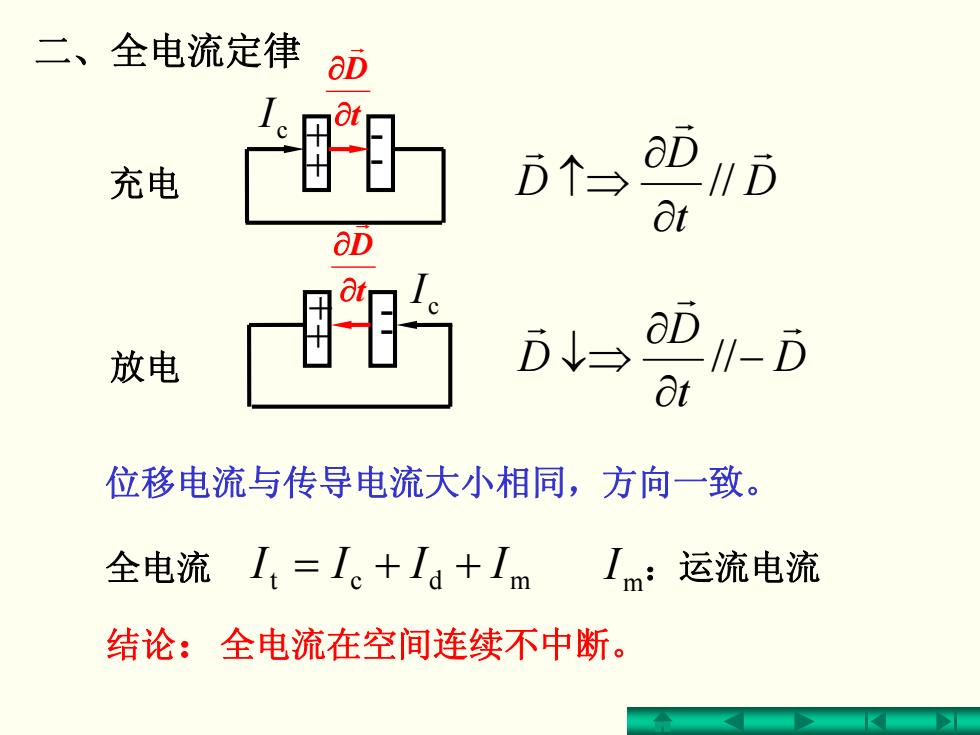
二、全电流定律 OD 充电 D个 aD 放电 BYODM-D at 位移电流与传导电流大小相同,方向一致。 全电流I=L。+Ia+Im 运流电流 结论:全电流在空间连续不中断
二、全电流定律 充电 D t D D r r r // ∂ ∂ ↑⇒ ++ -- c I t D ∂ ∂ r + + - - 放电 c I D t D D r r r − ∂ ∂ ↓⇒ // t D ∂ ∂ r mdct = + + IIII mI :运流电流 位移电流与传导电流大小相同,方向一致。 结论:全电流在空间连续不中断。 全电流

全电流定律 5i.dl==1.+1+1n 再来处理前面的问题无矛盾! di-1- 1-0fnd-2u 对比 gd-儿2s
∫∫∫ ⋅+=⋅ l S S tD IlH r r r r d d ∂ ∂ 若 I = 0 ∫∫∫ ⋅=⋅ l S S tD lH r r r r d d ∂ ∂ 对比 ∫∫∫ ⋅−=⋅ l S S tB lE r r r r i d d ∂ ∂ d mdct IIIIlHl ++==⋅ ∫ r r 全电流定律 再来处理前面的问题无矛盾! 1 2 c

运动电荷产生磁场: B= 4q×F (K<C) 4元 3 考虑变化电场贡献的磁场: B=, 9×(1-B2) 4πr0-B2sin297B=
c v r rvq B = − −× = β θβ μ β )sin1( )1( 4π 3 2322 2 0 r r r 3 0 4π r rvq B r r r × = μ (v<<c) + r r v q r B r θ 考虑变化电场贡献的磁场: 运动电荷产生磁场:

麦克斯韦对电磁学理论的贡献: 1.提出感应电场概念 2.提出位移电流概念 3.建立Maxwell方程组 4.预言电磁波的存在 (James Clerk Maxwell 1831-1879)
麦克斯韦对电磁学理论的贡献: (James Clerk Maxwell 1831-1879) 1. 提出感应电场概念 2. 提出位移电流概念 3. 建立Maxwell方程组 4. 预言电磁波的存在

三、位移电流性质 1.I,I。本质不同 2.电介质中 D=8E+P →j=60 aE Op 其中: E at at (1)E0 一纯粹为电场的变化,可以激发磁场! 8t 没有热效应! aP (2) 反映介质(分子)极化的变化,也可以 激发磁场! ·对高频电磁场,分子极矩方向高速变化,等效正负电 荷位置交替,有热效应一 微波炉! ·但是,与传导电流的热效应(焦耳热)完全不同!
三、位移电流性质 2. 电介质中 PEDr r r ε 0 += t P t E j ∂ ∂ + ∂ ∂ = r r r 0d ε 1. ,II cd 本质不同 —纯粹为电场的变化,可以激发磁场! 没有热效应! 其中: t E ∂ ∂ r 0 ( 1 ) ε t P ∂ ∂ r ( 2 ) —反映介质(分子)极化的变化,也可以 激发磁场! • 对高频电磁场,分子极矩方向高速变化,等效正负电 荷位置交替,有热效应——微波炉! • 但是,与传导电流的热效应(焦耳热)完全不同!
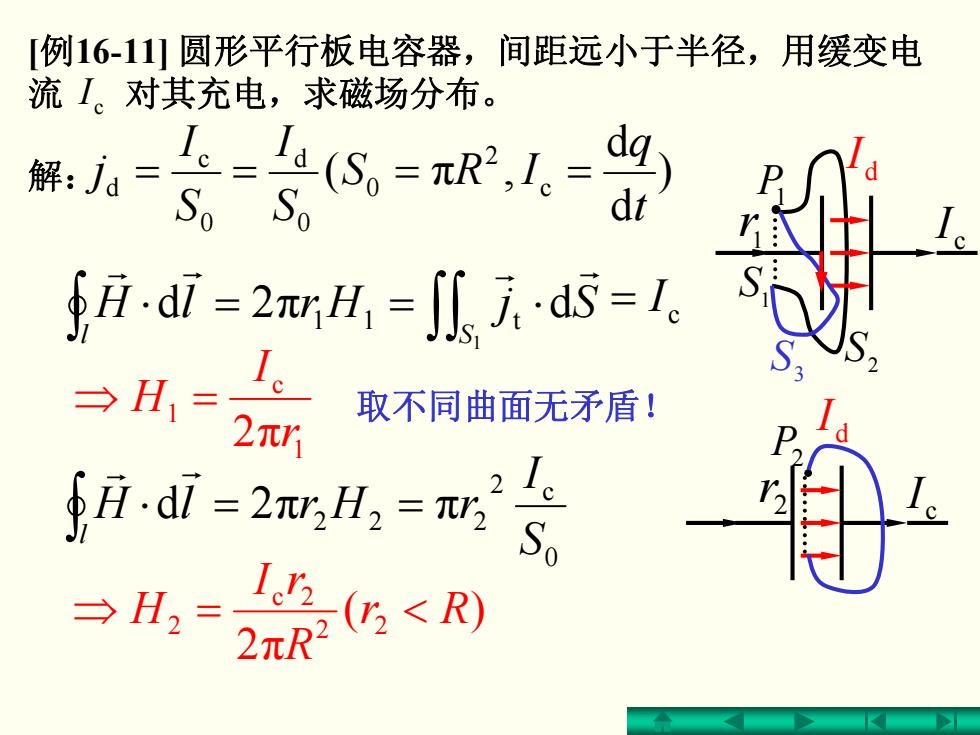
[例16-11)圆形平行板电容器,间距远小于半径,用缓变电 流I。对其充电,求磁场分布。 解:ja= ==R21,-) So So fidi=2rH,=八元.ds=1。 →H=2r 取不同曲面无矛盾! g2,=5 →,=袋低<风
解: P1 1 S c I d I 2 S 1r ) d d ( π , c 2 0 0 d 0 c d t q IRS S I S I j ==== ∫ ∫∫ ⋅==⋅ 1 2d π d 11 t l S SjHrlHr r r r c = I 1 c 1 2 π r I H =⇒ S 3 0 2 c ππ 222 2d S I rHrlH l ==⋅ ∫ r r )( 2 π 2 2 2c 2 Rr R rI H =⇒ < c I d I P2 2r [ 例16-11] 圆形平行板电容器,间距远小于半径,用缓变电 流 对其充电,求磁场分布。 c I 取不同曲面无矛盾!