
专题选读6平衡与迷落
专题选读6 平衡与涨落
平衡与涨落 一、统计分布规律是一种平均分布,存在涨落 C(m)表示某一种分布 出现的不同状态数 3) (微观状态数) P(m)则表示某一种分布 出现的概率。 L R
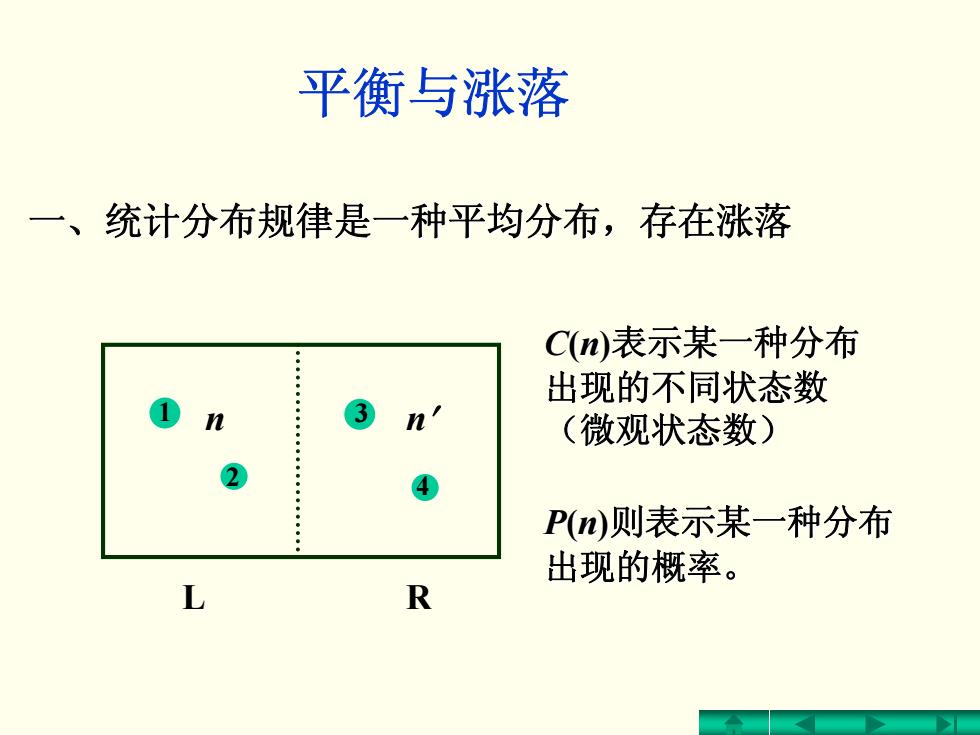
平衡与涨落 一、统计分布规律是一种平均分布,存在涨落 一、统计分布规律是一种平均分布,存在涨落 C(n)表示某一种分布 表示某一种分布 出现的不同状态数 出现的不同状态数 (微观状态数) (微观状态数) P(n)则表示某一种分布 则表示某一种分布 出现的概率。 n n′ 1 2 3 4 L R
统计分布规律 1 4 n n' C(n) P(n) L L L L 4 0 1 1/16 L L L R 3 1 L L R L 3 4 4/16 L R L L 3 1 R L L L 3 1 L L R R 2 2 L R L R 2 2 R L L R 2 2 L R R L 2 2 6 6/16 R L R L 2 2 R R L L 2 2 L R R R 3 R L R R 3 4/16 & R L R 3 R R R L 3 RR R R 1 0 1/16
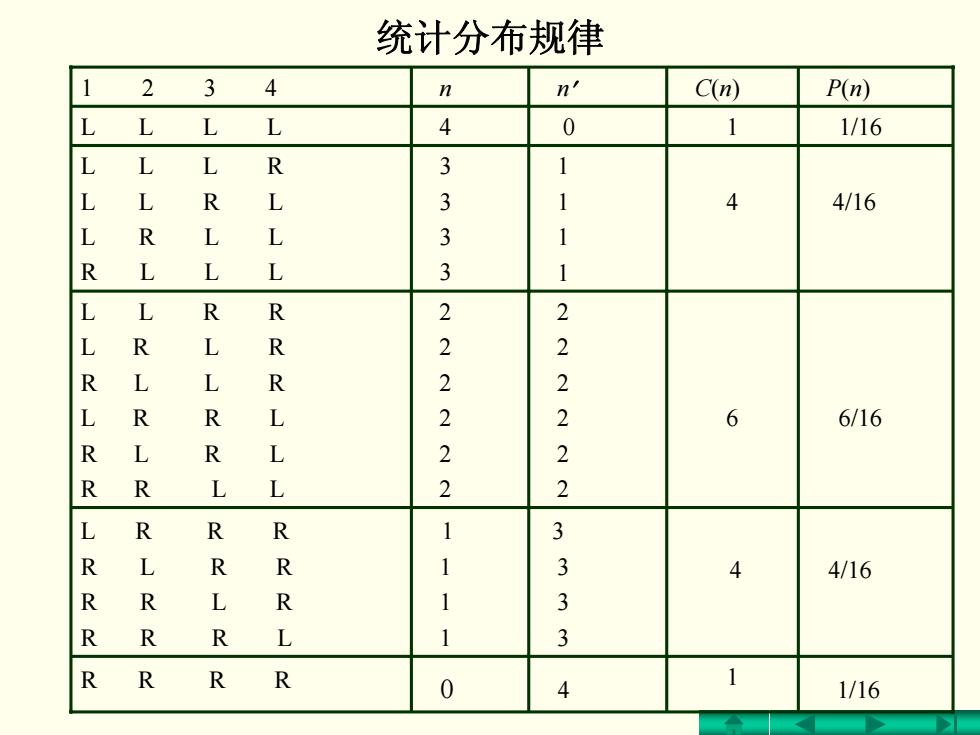
统计分布规律 1 2 3 4 n n′ C(n) P(n) 1 1/16 4/16 6/16 4/16 R R R R 0 4 1 1/16 4 6 4 0 1 1 1 1 2 2 2 2 2 2 3 3 3 3 4 3 3 3 3 2 2 2 2 2 2 1 1 1 1 L L L L L L L R L L R L L R L L R L L L L L R R L R L R R L L R L R R L R L R L R R L L L R R R R L R R R R L R R R R L

从上页表可见: ●四个分子在容器左右作均匀分布(即n=n'-2)的概率最 大,P(m)=P(2)=6/16; ●四个分子在容器一边分布(即n=4,n'=0或n=0,n= 4)的概率最小,P()=P(4)=1/16;这种相对平均分布的 偏离,叫涨落。 推广到N个粒子的情形,计算表明: ●随着分子总数的增多,对应n=NW2,n'=N/2的概率 迅速增大,而如n=0,n'=N的概率迅速减小; ●在分子总数为N的情况下,左室出现n个分子,右室出 现n'=N-n个分子的概率可按公式
从上页表可见: z 四个分子在容器左右作均匀分布(即n= n′ = 2)的概率最 大, P(n)=P(2)=6/16; z 四个分子在容器一边分布(即n= 4,n′ = 0或n= 0,n′ = 4)的概率最小, P(n)=P(4)=1/16;这种相对平均分布的 偏离,叫涨落。 N N nNn N nn N nP ⎟⎠⎞ ⎜⎝⎛ − ⎟ = ⎠⎞ ⎜⎝⎛ = 21 )!(! ! 21 !'! ! )( 推广到N个粒子的情形,计算表明: z 随着分子总数的增多,对应 n = N/2 ,n′ = N/2的概率 迅速增大,而如 n=0, n′=N 的概率迅速减小; z 在分子总数为N的情况下,左室出现n个分子,右室出 现 n′ = N-n 个分子的概率可按公式

P(n) ●概率P(n)是n的函数,称为二项 式分布。在n=N/2处P(n)有最大 值;气体分子全部收缩到左室中的 概率是1/2N。 N大 例如,若容器装有1mol气体,分子 数N=6.02×1023,则有 N小 1 1 26.02x1023 →0 2 说明分子全部收缩到左室中的情况 实际上不可能出现,而实际看到的 总是n=NW2的情况
z概率P(n) 是n 的函数,称为二项 式分布。在n=N/2处P(n)有最大 值;气体分子全部收缩到左室中的 概率是1/2N。 0 2 1 2 1 23 N = ×1002.6 → 例如,若容器装有1mol气体,分子 数N=6.02×1023,则有 说明分子全部收缩到左室中的情况 实际上不可能出现,而实际看到的 总是 n=N/2 的情况

问题:分子在容器中 的分布总是均匀的 吗? 答:事实并非如此, 如果将考察的体积减 小,例如考虑容器中 某处一个微小体积 △V,只要这个体积足 够小,就会实际上出 现△n偏离平均值△n= N△V/V的涨落现象
问题:分子在容器中 的分布总是均匀的 吗? 答:事实并非如此, 如果将考察的体积减 小,例如考虑容器中 某处一个微小体积 Δ V,只要这个体积足 够小,就会实际上出 现 Δn 偏离平均值 Δ n= N Δ V / V的涨落现象
又如,麦克斯韦分布对 于速度区间v到叶△y来 说,由于分子速率不断 fv) 变化,使得处在△v速率 区间中的分子数是变化 不定的。 而按分布定律算出的应 指分子数的平均值,在 任一瞬时处在此速率区 间中的分子数是可能偏 离此平均值的,这种偏 0 叶△y 离有时大,有时小,有 时正,有时负,这就是 涨落现象
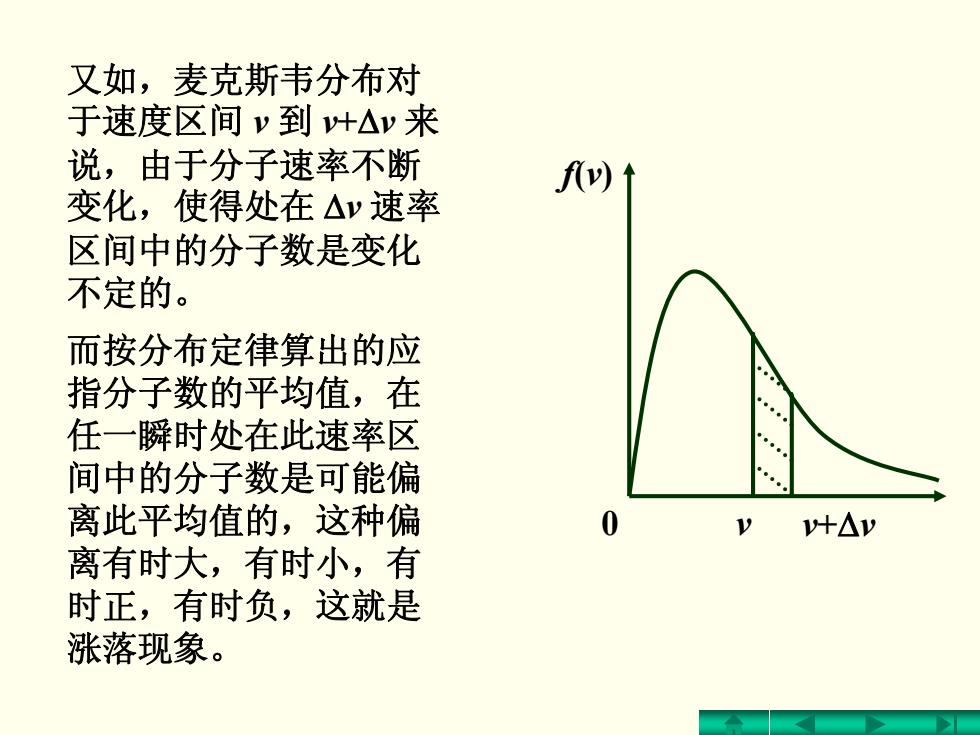
又如,麦克斯韦分布对 于速度区间 v 到 v + Δv 来 说,由于分子速率不断 变化,使得处在 Δv 速率 区间中的分子数是变化 不定的。 而按分布定律算出的应 指分子数的平均值,在 任一瞬时处在此速率区 间中的分子数是可能偏 离此平均值的,这种偏 离有时大,有时小,有 时正,有时负,这就是 涨落现象。 0 v v + Δ v f( v )

涨落 考虑容器中某处一个微小体积△八,则 W △n= △V 实际上,只要这个体积足够小,就会出现△n 偏离以上计算值(平均值)的涨落现象。 相对偏差定义为: (△n-△n)2 △n
涨落 实际上,只要这个体积足够小,就会出现Δn 偏离以上计算值(平均值)的涨落现象。 相对偏差定义为: n n nn Δ = Δ Δ−Δ )( 1 2 考虑容器中某处一个微小体积ΔV,则 V V N n Δ=Δ

公式的适用范围: 即适用体积△V中分子数△的涨落现象,又适用于 速率区间△v中分子△n的涨落现象。 例如,对△v来说,若△n=106,则, 1 =10-3 √△n 即分子数涨落是分子总数的千分之一。 此时,麦克斯韦分布基本正确
公式的适用范围: 即适用体积ΔV 中分子数 Δn 的涨落现象,又适用于 速率区间Δv 中分子Δn 的涨落现象。 例如,对 Δv 来说,若Δn =106,则, 即分子数涨落是分子总数的千分之一。 3 10 1 − = Δn 此时,麦克斯韦分布基本正确

如果△n=1,则 =1, 公n 这时麦克斯韦分布就完全不适用了。 可见对麦克斯韦函数来说,速率区间必须取得 足够大,使△v中包含的分子数△足够多,才 能不致产生对分布规律明显的涨落
如果Δn =1,则 这时麦克斯韦分布就完全不适用了。 可见对麦克斯韦函数来说,速率区间必须取得 足够大,使Δv中包含的分子数Δn足够多,才 能不致产生对分布规律明显的涨落。 ,1 1 = Δ n