
专题选读4:耦合振动和简正模
专题选读4:耦合振动和简正模

耦合振动和简正模 一个谐振子的振动由单一的固有频率表征。但是,一 个物理系统一般会有多个自由度,其实际振动表现是 非常复杂的,这样的系统通常能以许多不同的频率发 生振动。 振动模(简正模):系统 所具有的各式各样的振动 称为系统的振动模(简正 模)。系统的一般振动则 是各个简正模的叠加。 多自由度系统振动分析 思路:将一个连续的物 体看成是大量质点的组 合
耦合振动和简正模 振动模(简正模) 振动模(简正模):系统 所具有的各式各样的振动 所具有的各式各样的振动 称为系统的振动模(简正 称为系统的振动模(简正 模)。系统的一般振动则 模)。系统的一般振动则 是各个简正模的叠加。 是各个简正模的叠加。 多自由度系统振动分析 思路:将一个连续的物 体看成是大量质点的组 合。 一个谐振子的振动由单一的固有频率表征。但是,一 个物理系统一般会有多个自由度,其实际振动表现是 非常复杂的,这样的系统通常能以许多不同的频率发 生振动

例如,固体是由大量原子 和分子组成,而每个原子 (或分子)都在空间某一 平衡位置附近作振动,但 由于组成固体的原子(或 分子)间有较强的相互作 用,每个原子的运动都会 影响到邻近的原子。因 此,对组成固体的所有原 子而言,它们的运动实际 上是“耦合”在一起的,即 每个原子的运动是相互联 系、相互影响的
例如,固体是由大量原子 和分子组成,而每个原子 (或分子)都在空间某一 平衡位置附近作振动,但 由于组成固体的原子(或 分子)间有较强的相互作 用,每个原子的运动都会 影响到邻近的原子。因 此,对组成固体的所有原 子而言,它们的运动实际 上是 “耦合 ”在一起的,即 每个原子的运动是相互联 系、相互影响的
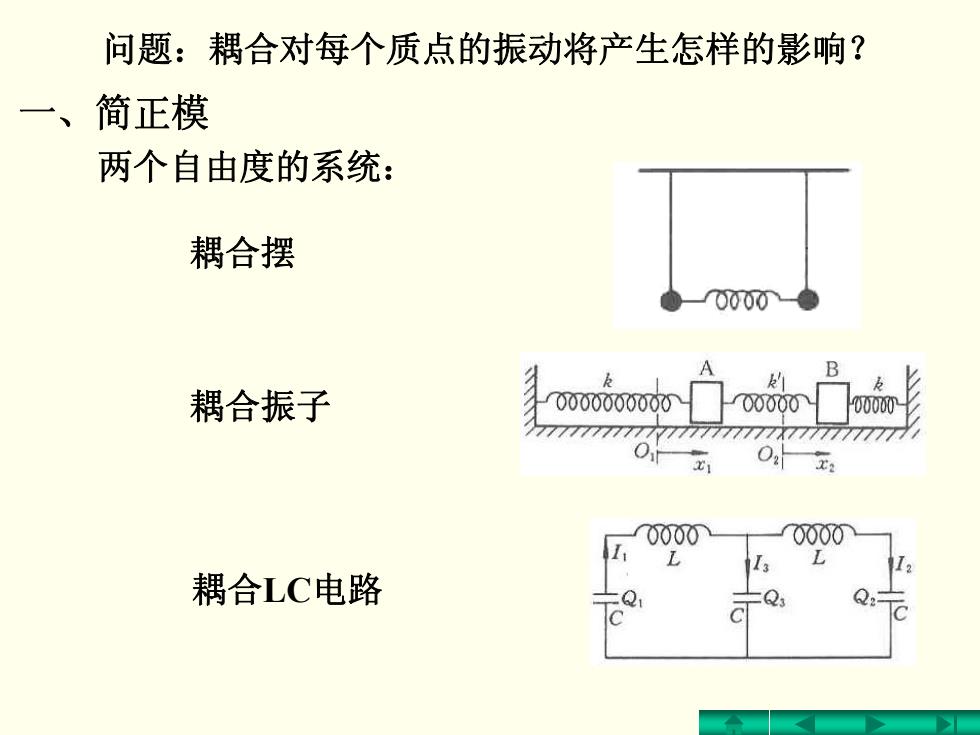
问题:耦合对每个质点的振动将产生怎样的影响? 一、 简正模 两个自由度的系统: 耦合摆 0000 耦合振子 0000000000 00000T 00000 777777777777777777777777777% 02x2 0000 0000 耦合LC电路 —Q
问题:耦合对每个质点的振动将产生怎样的影响? 一、简正模 两个自由度的系统: 耦合摆 耦合振子 耦合LC电路
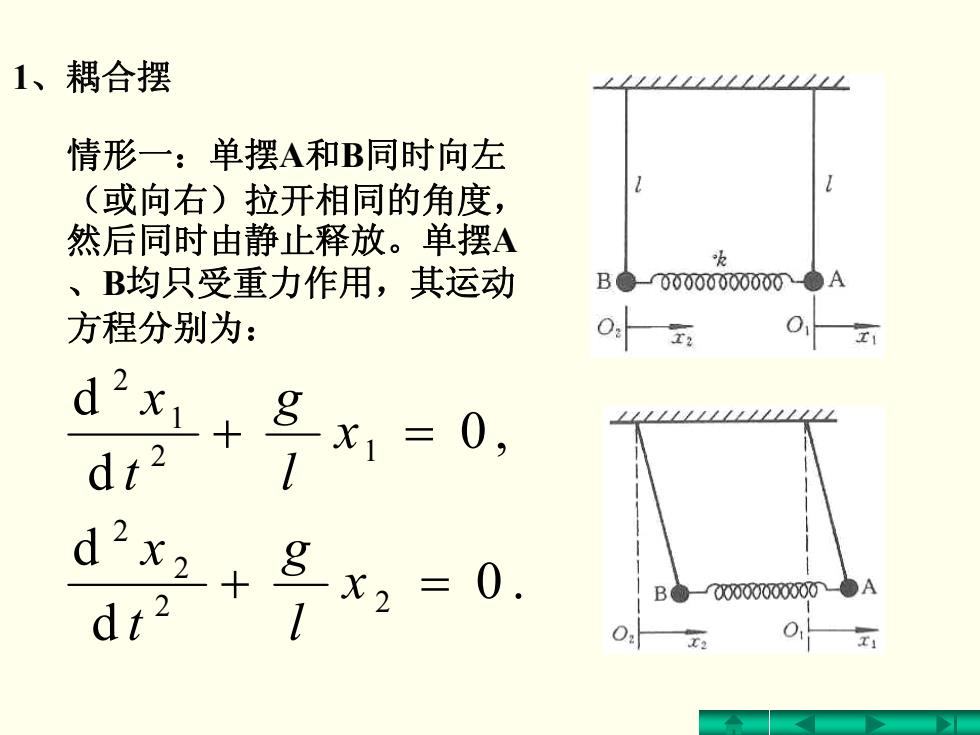
1、耦合摆 情形一:单摆A和B同时向左 (或向右)拉开相同的角度, 然后同时由静止释放。单摆A 、B均只受重力作用,其运动 B●-00000000000●A 方程分别为: O: 0, d2x1+8x1=0, dt2 2X2十 =0 B 00000000T-●A
1、耦合摆 情形一:单摆A和B同时向左 (或向右)拉开相同的角度, 然后同时由静止释放。单摆A 、B均只受重力作用,其运动 方程分别为: .0 d d ,0 dd 2 2 2 2 2 1 1 2 =+ =+ x l g t x x l g t x

解此方程得: x=xo coS @0t, 显然,这时A和B的运动就 是自由的无耦合的单摆的 X2=xo cos 0t, 运动,并且A和B的振幅、 相位都相等,两者间距也 式中 保持不变。这是耦合摆的 一种特殊运动状态,亦 00= 即耦合系统的一种简正模: 系统中每一个质点均以相 同频率和相位作简谐振动。 即为单摆作小角度摆动 时的角频率
解此方程得: 即为单摆作小角度摆动 时的角频率。 l g ω 0 = ,cos ,cos 02 0 01 0 txx txx ω ω = = 式中 显然,这时 A 和 B的运动就 是自由的无耦合的单摆的 运动,并且 A 和 B的振幅、 相位都相等,两者间距也 保持不变。这是耦合摆 的 一种特殊运动状态,亦 即耦合系统的一种简正模: 系统中每一个质点均以 相 同频率和相位 作简谐振动

情形二:把A和B同时沿相反 的方向拉开相同的角度,然后 同时由静止释放。此时,A、 B不仅受重力和绳的张力,而 且受连接两摆的弹簧施加的力 B●》》-●A 作用,其运动方程为: 02 工2 d2x1+8x1+ 2k dt2 1=0, m d2x2 2k dt2 +gx2+ -x2=0 m 上式可简写为: dt2 x1=0, d2x2+02x2=0, dt2
情形二:把A和B同时沿相反 的方向拉开相同的角度,然后 同时由静止释放。此时,A、 B不仅受重力和绳的张力,而 且受连接两摆的弹簧施加的力 作用,其运动方程为: .0 2 d d ,0 2 dd 2 2 2 2 2 2 1 1 1 2 =++ =++ x m k x l g t x x m k x l g t x 上式可简写为: ,0' dd ,0' dd 2 2 2 2 2 1 2 2 1 2 =+ =+ x t x x t x ω ω

。- 式中 利用初始条件t=0时, ==x及班=血=0 dt dt 得x1=-x0c0s0't, X2=xo coS @'t. 由此可见,在这种情况下,A、B仍以相同频率ω作 简谐振动,但由于弹簧的作用,使频率o>@,并且 在运动中A和B之间的相位差始终为π
由此可见,在这种情况下, A 、 B仍以相同频率ω′ 作 简谐振动,但由于弹簧的作用,使频率ω′ > ω0 ,并且 在运动中 A 和 B之间的相位差始终为 π 。 .'cos ,'cos 02 1 0 txx txx ω ω = = − 2/1 ) 2 (' m k l g ω += t = 0 及 0, d d d d , 21 0201 ===−= t x t x xxxx 式中 利用初始条件 时, 得

综合情形一和情形二,可得以下结论: 具有两个自由度的系统可以有两种简正模,即 低频模式:X1=x2,01=00= 此时,两质点作同相位的简谐振动,振动频率相同 且等于无耦合时自由振动的频率。 此时,两质点作频率相同但相位相反的简谐振动,但 振动频率将大于无耦合时自由振动的频率
综合情形一和情形二,可得以下结论: 具有两个自由度的系统可以有两种简正模,即 低频模式: 此时,两质点作同相位的简谐振动,振动频率相同 且等于无耦合时自由振动的频率。 此时,两质点作频率相同但相位相反的简谐振动,但 振动频率将大于无耦合时自由振动的频率。 高频模式: l g xx , ωω 0l21 === 2/1 1 h2 ) 2 (', m k l g xx ωω +==−=
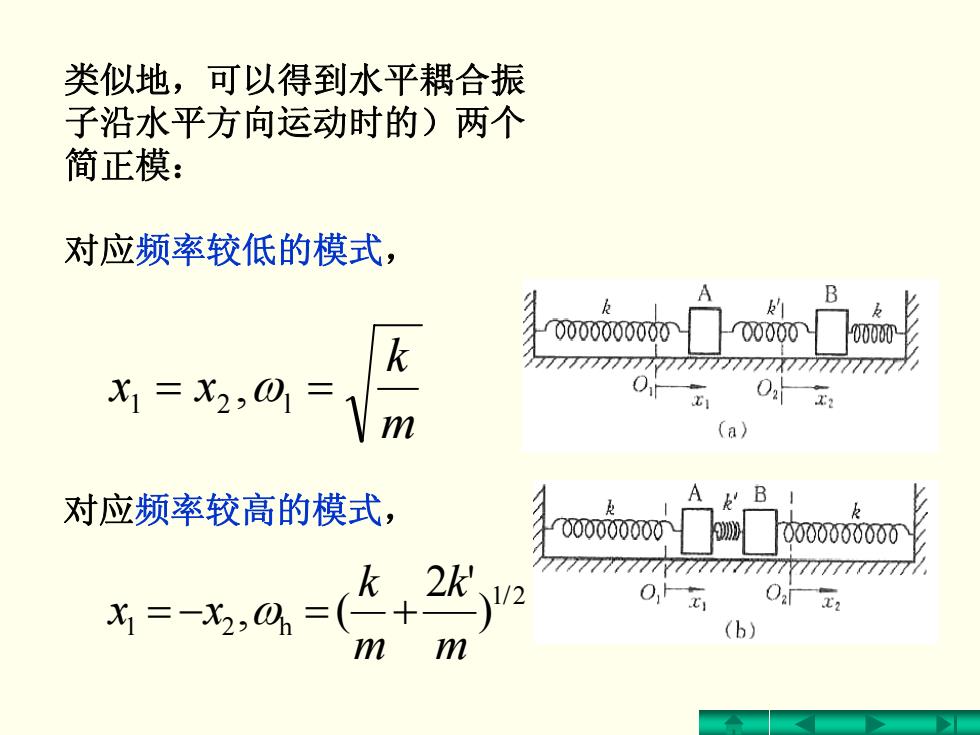
类似地,可以得到水平耦合振 子沿水平方向运动时的)两个 简正模: 对应频率较低的模式, B 0000000000T 00000 k x=%2:0=m 02x2 (a)》 对应频率较高的模式, 000000000Ty 0000000000 =,=+2 7777777777777777777777777777 (b)
类似地,可以得到水平耦合振 子沿水平方向运动时的)两个 简正模: 对应频率较低的模式 , m k xx , ωl21 == 对应频率较高的模式 , 2/1 h21 )'2 (, m k m k xx ω +=−=