专题选读13非线性光学现象
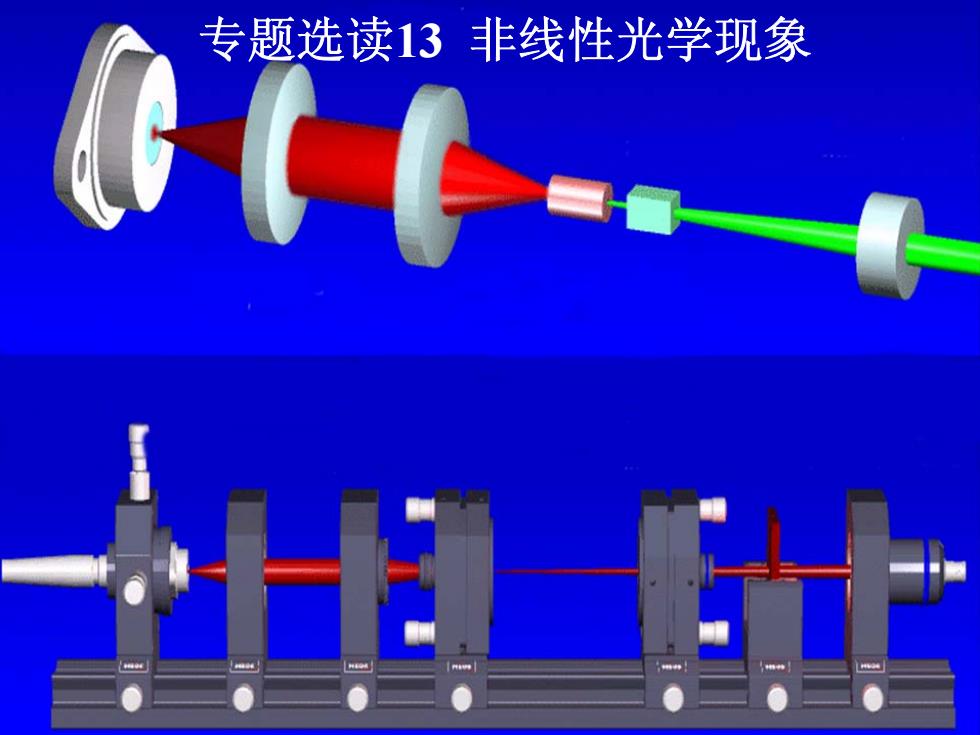
专题选读13 非线性光学现象

非线性光学现象 线性光学(普通波动光学) 当光在物质中传播与物质发生相互作用时,通常假定物 质原子对光波电磁场的响应是成正比或线性的,光在介 质中传播满足独立性和叠加性,这理论称为线性光学。 非线性光学 当强激光进入介质时,原子对光波电磁场的响应不仅决 定于场强的一次项,也与场强的高次项有关,即响应一 般是非线性的,探讨这类与光的非线性现象有关的规律、 理论和应用的学科,称为非线性光学
非线性光学现象 线性光学(普通波动光学) 线性光学(普通波动光学) 非线性光学 当光在物质中传播与物质发生相互作用时,通常假定物 当光在物质中传播与物质发生相互作用时,通常假定物 质原子对光波电磁场的响应是成正比或线性的,光在介 质原子对光波电磁场的响应是成正比或线性的,光在介 质中传播满足独立性和叠加性,这理论称为线性光学。 质中传播满足独立性和叠加性,这理论称为线性光学。 当强激光进入介质时,原子对光波电磁场的响应不仅决 定于场强的一次项,也与场强的高次项有关,即响应一 般是非线性的,探讨这类与光的非线性现象有关的规律、 理论和应用的学科,称为非线性光学

弱光使介质极化而产生的极化强度P与光矢量在量值 上有如下关系: P=EoxE=aE 在强光作用下,介质的极化强度与光矢量量值一般有下 列关系: P=aE+BE2+E3+.. 式中a,B,%…是与介质有关的系数。 理论证明: BE2 YE3 E aE BE2 E
Ea E E E E E ≈⋅⋅⋅≈≈ 2 2 3 β γ α β ⋅⋅⋅+++= 32 γβα EEEP 在强光作用下,介质的极化强度与光矢量量值一般有下 列关系: 式中α,β,γ,... 是与介质有关的系数。 理论证明: EEP r r r == αχε e0 弱光使介质极化而产生的极化强度 与光矢量 在量值 上有如下关系: P r E r

式中E代表介质原子内的电场强度,其数量级约为 1010~1011V/m。 对于普通光源发射的光波,光矢量E103~104Vm, E/E,<1,所以近似有P≈aE。 对于强激光,光矢量E109~1012Vm,这时不能略 去P中所包含的E的高次项了。 一、倍频和混频 设入射到介质中的强光光矢量的大小 E=Eo cos ot
式中Ea代表介质原子内的电场强度,其数量级约为 1010~1011V/m。 对于普通光源发射的光波,光矢量E ≈103 ~104V/m, E/Ea<<1, 所以近似有P≈αE。 对于强激光,光矢量E ≈109 ~1012V/m,这时不能略 去P中所包含的E的高次项了。 一、倍频和混频 设入射到介质中的强光光矢量的大小 ,cos 0 = ωtEE

介质响应的极化强度 P=aE cos ot+BE"cos2 ot+E cos3 wt+... 为方便计,略去(E)3以上各项时有 P-aE cost+(+cos2t) af,cos cos2o 上式第一项是常量,相当于使介质产生恒定的电矩,使 其相对的表面上出现恒定的极化面电荷。这种由振动的 交变电场得到一个恒定的电场,称为光学整流
介质响应的极化强度 = + + ωγωβωα tEtEtEP ⋅⋅⋅+ 3 3 0 2 2 0 0 cos cos cos 为方便计,略去 (E 0 ) 3以上各项时有 tEtEE EtEP t ωβωαβ βωα ω 2cos 2 1 cos 2 1 )2cos1( 2 1 cos 2 0 0 2 0 2 0 0 += + = ++ 上式第一项是常量,相当于使介质产生恒定的电矩,使 其相对的表面上出现恒定的极化面电荷。这种由振动的 交变电场得到一个恒定的电场,称为光学整流
第二项是频率等于入 射光频率的极化强度 振动分量,是基频项, 它表明介质原子发射 与入射光有相同的频 率的次极光波; 第三项是频率等于入 射光频率两倍的极化 表面 强度振动分量,它表 明介质原子还发射频 率等于入射光频率两 倍的次级光波,这一 现象称为光学倍频
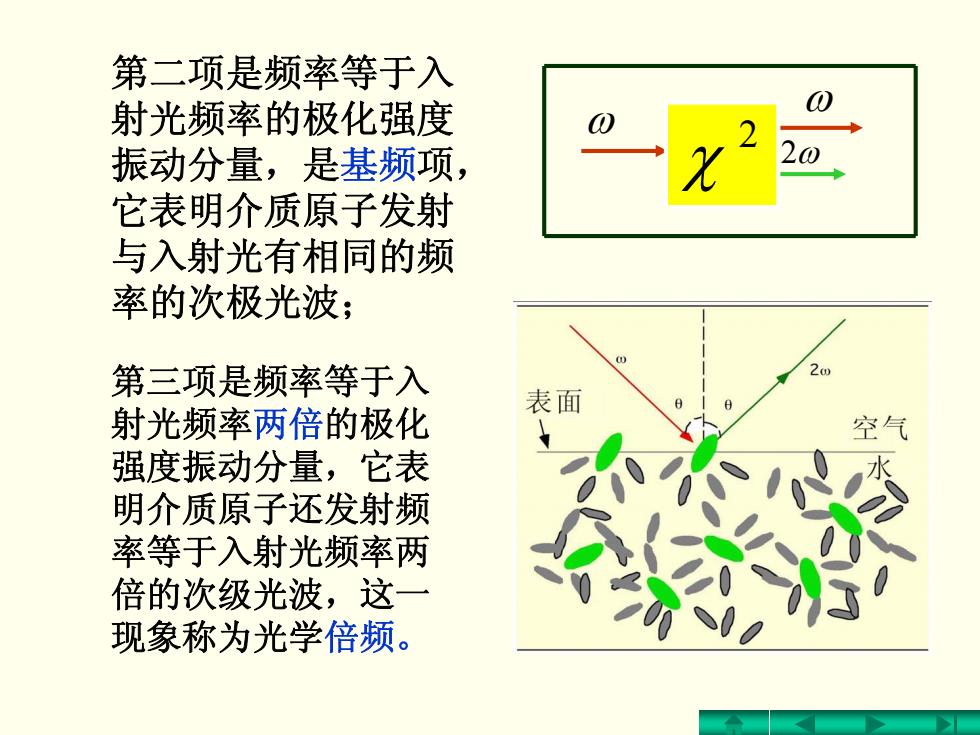
第二项是频率等于入 射光频率的极化强度 振动分量,是基频项, 它表明介质原子发射 与入射光有相同的频 率的次极光波; 第三项是频率等于入 射光频率两倍的极化 强度振动分量,它表 明介质原子还发射频 率等于入射光频率两 倍的次级光波,这一 现象称为光学倍频。 2 χ ω ω 2 ω

光学混频 当不同频率的两束强光 E=Eo cos@t, E2=E20c0S02t. Dvis 在介质中相遇时,则介质 的极化强度P中除包含直 流、基频、倍频各项外, 还有和频(0+),差频 |010,项出现,这一现 象称为光学混频
当不同频率的两束强光 光学混频 ⎩ ⎨ ⎧ = = .cos ,cos 202 2 101 1 tEE tEE ω ω 在介质中相遇时,则介质 的极化强度 P中除包含直 流、基频、倍频各项外, 还有和频 ( ω1+ ω2 ),差频 |ω1 - ω2|项出现 ,这一现 象称为光学混频

二、自聚焦效应 在强光的情况下,介质的折射率不只与入射光的 频率有关,还与光矢量的大小有关。在非线性条 件下,定义各向同性介质的介电常数 dD d 6= dE (80E+P)=80+ d P dE dE 且 P=E+BE2+yE3+·.. 考虑到各向同性介质的B0和n=√8, 可求得近似式n=n。+n1E2
二、自聚焦效应 在强光的情况下,介质的折射率n不只与入射光的 频率有关,还与光矢量的大小有关。在非线性条 件下,定义各向同性介质的介电常数 ⋅⋅⋅+++= == +=+ 2 3 0 0 , d d ( ) dd dd EEEP E P PE EE D γβα ε ε ε 且 考虑到各向同性介质的β=0和 r n = ε 可求得近似式 2 += 10 Ennn

式中n就是通常的介质折 射率,n称为非线性折射 系数。上式表明折射率随 光强而变化。 自聚焦:因为激光束截 面沿横向的光强分布不 均匀,在轴线上光强最 大,一般呈现高斯分布, 因而使折射率也作同样 的分布。这就在介质内 形成一类似凸透镜的结 构,使光束向轴上汇聚 自聚焦仪 ,这一现象称为自聚焦
式中 n就是通常的介质折 射率, n 1称为非线性折射 系数。上式表明折射率随 光强而变化。 自聚焦:因为激光束截 面沿横向的光强分布不 均匀,在轴线上光强最 大,一般呈现高斯分布, 因而使折射率也作同样 的分布。这就在介质内 形成一类似凸透镜的结 构,使光束向轴上汇聚 ,这一现象称为自聚焦。 自聚焦仪
三、双光子吸收现象 真空管 石英窗 在弱光入射条件下, 原子受激发时每次 只吸收一个光子, 并且只有当原子两 能级的差与入射光 子的频率满足玻尔 频率公式时,吸收 才能发生。吸收一个 光电效应的光电管实验装置 光子的爱因斯坦光电 效应方程为: 光电管在阴极金属表面逸出 1 的电子称为光电子。电路中 hv= mw2+A 出现的电流形成光电流。 2
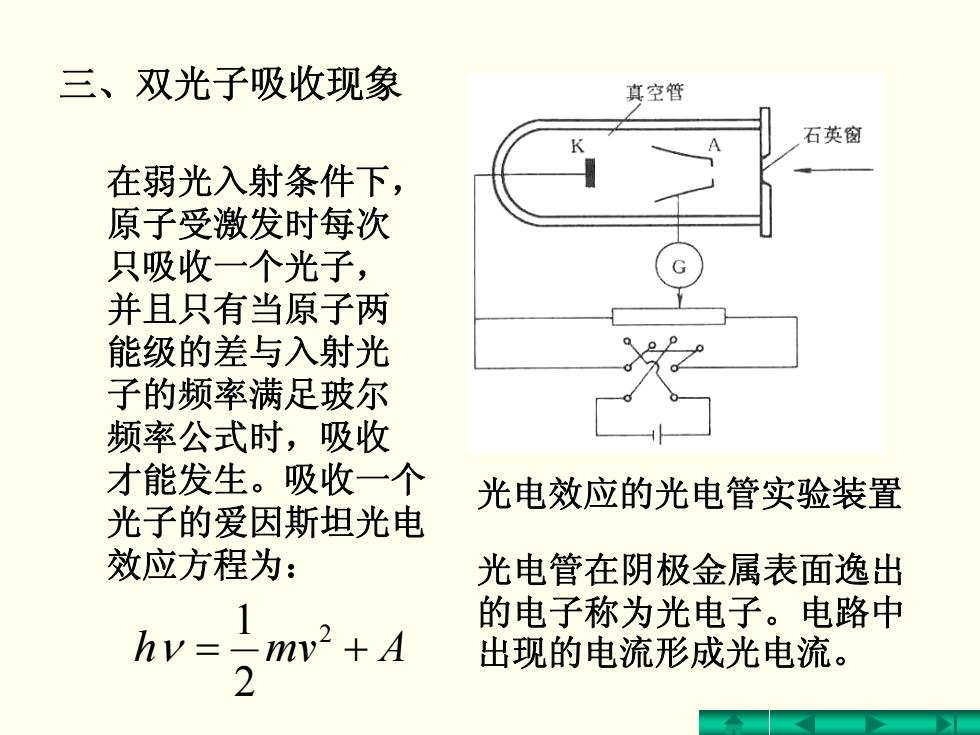
三、双光子吸收现象 在弱光入射条件下, 原子受激发时每次 只吸收一个光子, 并且只有当原子两 能级的差与入射光 子的频率满足玻尔 频率公式时,吸收 才能发生。吸收一个 光子的爱因斯坦光电 效应方程为: += Amvh 2 2 1 ν 光电效应的光电管实验装置 光电效应的光电管实验装置 光电管在阴极金属表面逸出 的电子称为光电子。电路中 出现的电流形成光电流