
第15章兹介质 §15.1顺磁性和抗磁性 §15.2磁化强度和磁化电流 §15.3介质中的磁场 磁场强度 §15.4铁磁性
§15.1 顺磁性和抗磁性 §15.2 磁化强度和磁化电流 §15.3 介质中的磁场 磁场强度 §15.4 铁磁性 第 15 章 磁介质

§15.3介质中的磁场 磁场强度 B=Bo+B' B。:外磁场 B:磁化电流产生 一、介质中磁场的高斯定理 月8,ds=0∯B.d5=0→∯B.ds=0 二、磁场强度 介质中磁场的安培环路定理 fB.di=4∑1,+4∑I 1:传导电流?磁化电流
§15.3 介质中的磁场 磁场强度 += BBB ′ r r r 0 一、 介质中磁场的高斯定理 0d 0d 0 =⋅ ′ =⋅ ∫∫∫∫ SBSBs s r r r r =⋅⇒ 0d ∫∫ SBs r r 二、 磁场强度 介质中磁场的安培环路定理 ∫ ∑ +=⋅ ∑ ′ i i i i l d 0 μμ 0 IIlB r r Ii:传导电流 Ii′:磁化电流 B′ r :磁化电流产生 B0 r :外磁场
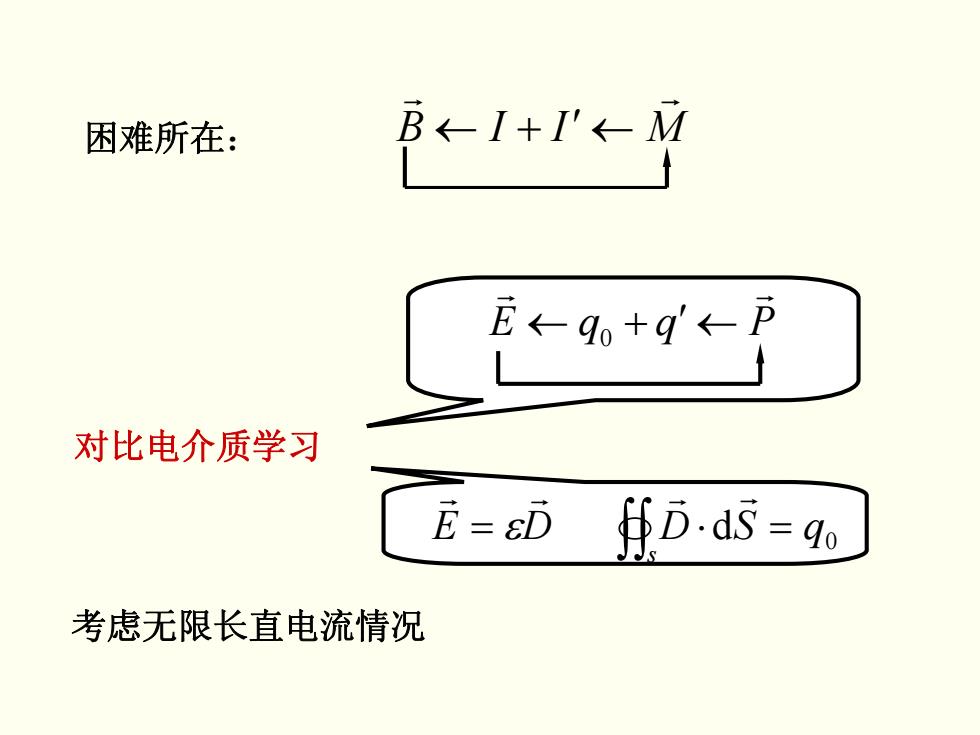
困难所在: B←-I+'←M E←9+g←p 对比电介质学习 E=&D D.ds=go 考虑无限长直电流情况
∫∫ = =⋅ s qSDDE 0 d r r r r ε PqqE r r 0 +← ′ ← MIIB r r 困难所在: +← ′ ← 对比电介质学习 考虑无限长直电流情况
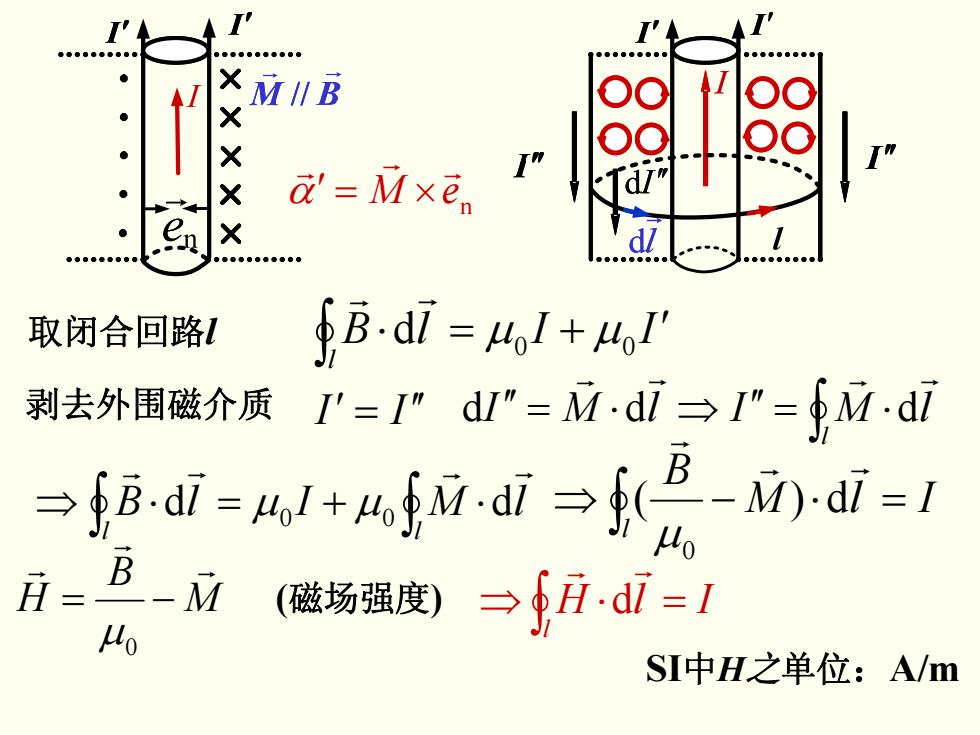
d=Mxe。 取闭合回路1 B.d7 =Hol+o 剥去外围磁介质1'=1”d”=Mdi→1”=M.dl →f8-di=41+4fw.i→f五-0-ai- 月=B- Mo (磁场强度)→开d=1 SI中H之单位:A/m
IIlB l +=⋅ ′ ∫ 00 d μμ r r I′ = I′′ ∫ ′′ ⇒⋅= ′′ ⋅= l lMIlMI r r r r dd d ∫ ∫ ⋅+=⋅⇒ l l lMIlBr r r r d d μμ 00 ∫ =⋅−⇒ l IlM B r r r d)( μ0 M B H r r r −= μ0 (磁场强度) SI中H之单位:A/m ∫ =⋅⇒ l IlHr r d n eM r r r α′ ×= 取闭合回路l 剥去外围磁介质

三、各向同性的磁介质 实验公式:M=Xmi Xm:介质的磁化率 B=4(i+M)=4,(1+Xm)H 4=1+Xm →B=44,i=ǖ 4:介质的相对磁导率 山:介质的磁导率 4.>1Xm>0顺磁质 4<1Xm<0抗磁质
三、 各向同性的磁介质 MHB H r r r r )1()( μ0 0 +=+= χμ m μr 1+= χ m HHBr r r r0 ==⇒ μμμ 0 1 0 1 r m r m > χμ μ χ 抗磁质 顺磁质 HMr r 实验公式: = χ m χ m :介质的磁化率 μr :介质的相对磁导率 μ :介质的磁导率

利用磁高斯定理和安培环路定理可证明:在不 同介质交界面两侧的磁场满足如下边界条件: Bin=B2n B H. H=H2 B,/
B1 r B2 r H1 r H2 r n r t2t1 n2n1 HH BB = = 利用磁高斯定理和安培环路定理可证明:在不 同介质交界面两侧的磁场满足如下边界条件:

[例15-2]求磁介质中的磁化强度、磁感应强度及其表面磁 化电流线密度。 解: Hdi=1 2xrH-1 →H= 2元r M=Xmi=(4,-1)i M=(4,-1)H=4,-1☑ 2元r :B=4o4,H= →B=44,2r 4-4-5R .=M×en END
[ 例15-2] 求磁介质中的磁化强度、磁感应强度及其表面磁 化电流线密度。 ∫ =⋅ l IlHr r d 2 π = IrH r I H 2 π =⇒ HM H r r r )1( m μχ r −== πr2 )1( )1( r r I M H − =−= μ μ HHBr r r Q r0 == μμμ r I B 2 π =⇒ μμ r0 n eM r r r Q α ′ ×= 1 r 1 2 π )1( R − I ′ = μ α 2 r 2 2 π )1( R − I ′ = μ α 解: END