
第18章电滋波 §18.1电磁波波动方程 §18.2电磁波的性质 §18.3振荡电偶极子的辐射赫兹实验
第 18 章 电磁波 §18.1 电磁波波动方程 §18.2 电磁波的性质 §18.3 振荡电偶极子的辐射 赫兹实验
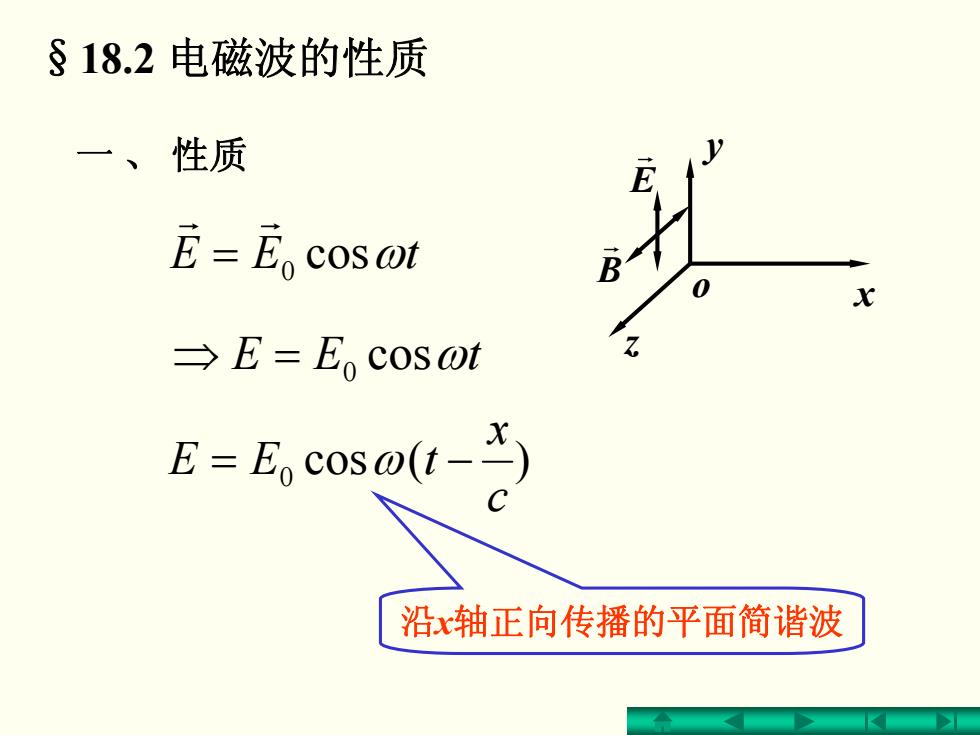
§18.2电磁波的性质 一、性质 E=E cosot →E=E cos ot E=Eo coso(t-) 沿x轴正向传播的平面简谐波
§18.2 电磁波的性质 一 、 性质 0 cosωtEE r r = ⇒ = 0 cosωtEE )(cos 0 c x = ω tEE − 沿x轴正向传播的平面简谐波 E r B r o x y z

OE aH 可证: 8x 二一oat E=E cos(- 1 E →H= d=5 cosot-之=,cos01-。 uoc Ho= E0 1 Moc 沿x轴负向传播: E=Eocoso(t+%) H=-Hocos(+
)(cos)(cosd 1 0 0 0 0 c x tH c x t c E t x E H = =− − ∂ ∂ −=⇒ ∫ ω ω μ μ 0 0 0 0 0 0 E c E H μ ε μ == 沿x轴负向传播: )(cos 0 c x −= ω tHH + )(cos 0 c x = ω tEE + 可证: t H x E ∂ ∂ −= ∂ ∂ μ0 )(cos 0 c x = ω tEE − 00 1 εμ c =

E=Eo cos@(t-) H=Ho coso(t- 性质:1.横波性 E,i⊥u 2.偏振性 E⊥i,tWE×i 3.E,i同相位 H24B-A
性质: 1. 横波性 uHE 2. 偏振性 r r r , ⊥ )(cos 0 c x = ω tEE − )(cos 0 c x = ω tHH − HEuHE r r r r r ⊥ // , × 3. HE 同相位 r r , 1 0 0 E c = BEH = μ ε z E r → r H u r H r E r o y x

二、 坡印廷矢量 电磁波的能流密度: S=wu 利用:u= - 2 5H-?yaed →S=EH
二、 坡印廷矢量 电磁波的能流密度 : 2 2 2 1 2 1 +== με HEwwuS ⇒ = EHS H εμμ EH 2 1 2 1 2 = μεε HEE 2 1 2 1 2 = u με HE με = , = 1 利用:

SI/u/E×i 台S=Exi E 电磁波强度: 1=5=,eE 2\u →S=EH
HEuS r r r r //// × HES r r r ×=⇒ S r E r H r 电磁波强度: = 00 == uwHEE 20 21 21 με 2 ESI μ ε == ⇒ = EHS
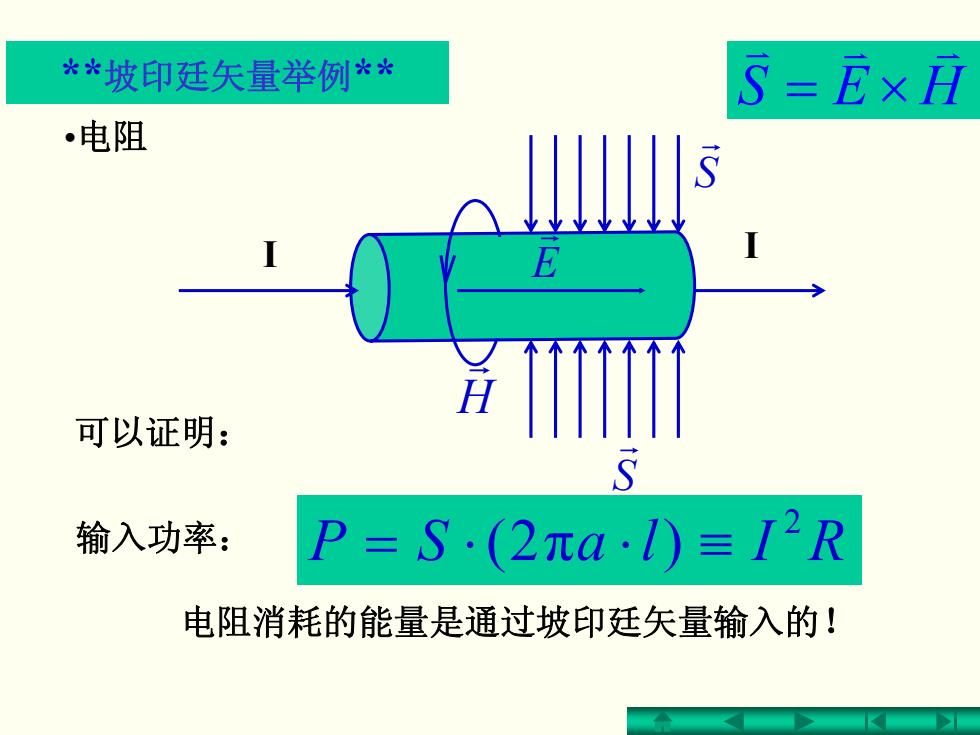
**坡印廷矢量举例** S=E×月 •电阻 可以证明: S 输入功率: P=S(2πa·1)≡I2R 电阻消耗的能量是通过坡印廷矢量输入的!
**坡印廷矢量举例** •电阻 I I H r E r S r S r 可以证明: RIlaSP 2 2( π ) ≡⋅⋅= 电阻消耗的能量是通过坡印廷矢量输入的! HES v v v ×= 输入功率:
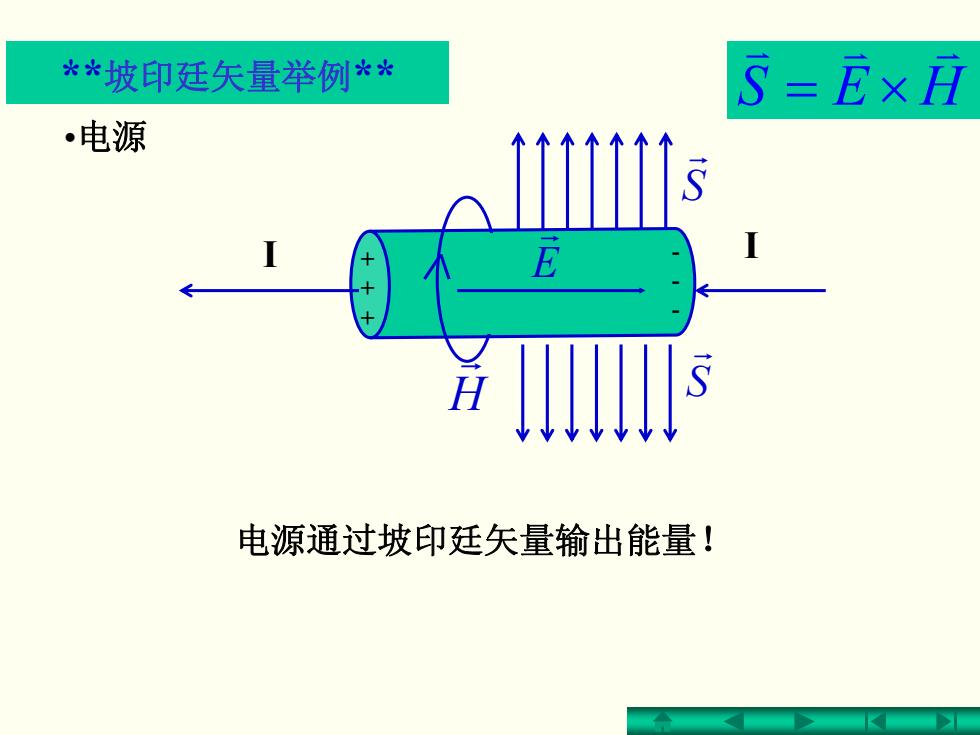
**坡印廷矢量举例** 5=尼×i •电源 电源通过坡印廷矢量输出能量!
- - - + + + •电源 I I H r E r S r S r 电源通过坡印廷矢量输出能量! HES v v v **坡印廷矢量举例** ×=
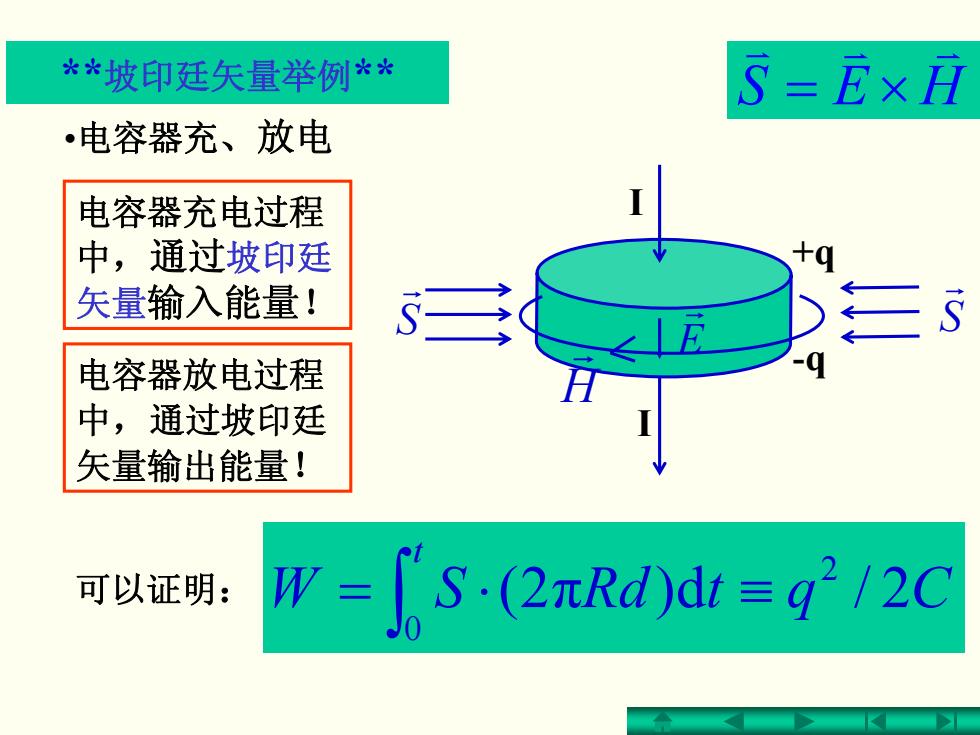
**坡印廷矢量举例** S=E×月 •电容器充、放电 电容器充电过程 中,通过坡印廷 矢量输入能量! 电容器放电过程 中,通过坡印廷 矢量输出能量! 可以证明: W=S:(2πRd)dt≡q2/2C
+q -q •电容器充、放电 I I E r S r S r 电容器充电过程 中,通过坡印廷 矢量输入能量! H r 电容器放电过程 中,通过坡印廷 矢量输出能量! 可以证明: CqtRdSW t 2( π 2/d) 2 0 ≡⋅= ∫ **坡印廷矢量举例** HES v v v ×=

三、辐射压强 (E-me) W 质量密度: 动量密度:p=B-”(:E2=p2c2+mc)) E PCAS F 辐射压强: F pc=w △S △S △S
三、 辐射压强 质量密度: 动量密度: )( 2 2 mcE c w m Q == ( ) 2 2 0 222 cmcpE c w c E p Q +=== 辐射压强: c F ΔS wpc SSpc SF == ΔΔ = Δ