
第21章量子光学基出 §21.0引言 §21.1热辐射黑体辐射 §21.2普朗克的能量子假说和黑体辐射公式 §21.3光的粒子性 §21.4康普顿散射 §21.5氢原子光谱 Bohr理论 §21.6光的辐射和吸收 §21.7激光
第 21 章 量子光学基础 §21.1 热辐射 黑体辐射 §21.2 普朗克的能量子假说和黑体辐射公式 §21.3 光的粒子性 §21.4 康普顿散射 §21.5 氢原子光谱 Bohr 理论 §21.6 光的辐射和吸收 §21.7 激光 §21.0 引言

§21.5氢原子光谱 Bohr理论 一、经典原子模型及其困难 1.汤姆逊父子的面包夹葡萄干模型(1902-1904) 整个原子呈胶冻状的球体,正 电荷均匀分布于球体上,而电 子镶嵌在原子球内,在各自的 平衡位置作简谐振动并发射同 频率的电磁波。 简化为谐振子模型一能解释可 见光区的光谱,不能说明红外、 紫外光谱。 ~10-10m
§21.5 氢原子光谱 Bohr 理论 一、经典原子模型及其困难 1. 汤姆逊父子的面包夹葡萄干模型( 汤姆逊父子的面包夹葡萄干模型(1902-1904) - - - - - - r~10-10m 整个原子呈胶冻状的球体,正 电荷均匀分布于球体上,而电 子镶嵌在原子球内,在各自的 平衡位置作简谐振动并发射同 频率的电磁波。 简化为谐振子模型—能解释可 见光区的光谱,不能说明红外、 紫外光谱
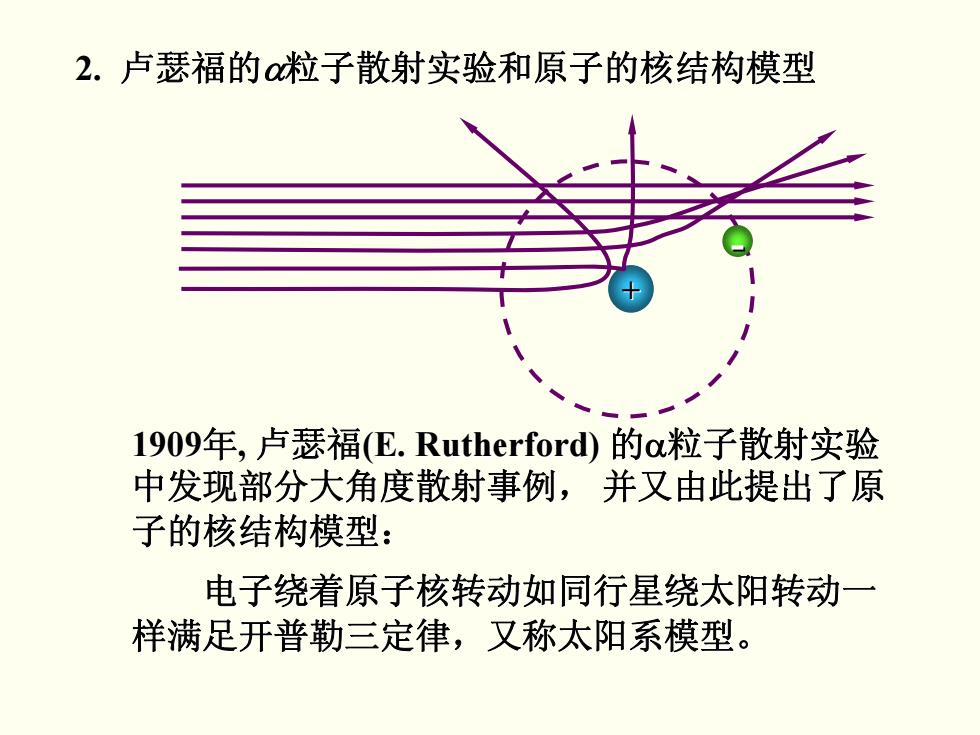
2.卢瑟福的粒子散射实验和原子的核结构模型 1909年,卢瑟福(E.Rutherford)的o粒子散射实验 中发现部分大角度散射事例,并又由此提出了原 子的核结构模型: 电子绕着原子核转动如同行星绕太阳转动一 样满足开普勒三定律,又称太阳系模型
+ - 1909年, 卢瑟福(E. Rutherford Rutherford) 的α粒子散射实验 中发现部分大角度散射事例, 中发现部分大角度散射事例, 并又由此提出了原 又由此提出了原 子的核结构模型: 子的核结构模型: 2. 卢瑟福的α粒子散射实验和原子的 粒子散射实验和原子的核结构模型 电子绕着原子核转动如同行星绕太阳转动一 电子绕着原子核转动如同行星绕太阳转动一 样满足开普勒三定律,又称太阳系模型。 样满足开普勒三定律,又称太阳系模型

3. 经典原子模型的困难 核结构模型很好地解释了粒子散射实验,但却 使经典理论陷入困境: (1)原子的稳定性问题 按照经典电磁理论加速带电粒子一定要辐射电磁 波,使得电子的动能越来越小,最后电子被吸引 到原子核上。原子是不稳定的。 (2)原子光谱的线状光谱问题 若电子运动的周期为T,发射的电磁波的周期也 应该是T,电子的周期由于运动半径越来越小是 连续变化的,所以按卢瑟福的的原子模型辐射 的电磁波应该是连续谱
核结构模型很好地解释了 核结构模型很好地解释了 α粒子散射实验,但却 粒子散射实验,但却 使经典理论陷入困境: 使经典理论陷入困境: ( 1)原子的稳定性问题 )原子的稳定性问题 ( 2)原子光谱的线状光谱问题 )原子光谱的线状光谱问题 按照经典电磁理论加速带电粒子一定要辐射电磁 按照经典电磁理论加速带电粒子一定要辐射电磁 波,使得电子的动能越来越小,最后电子被吸引 波,使得电子的动能越来越小,最后电子被吸引 到原子核上。原子是不稳定的。 到原子核上。原子是不稳定的。 若电子运动的周期为 若电子运动的周期为 T ,发射的电磁波的周期也 发射的电磁波的周期也 应该是 T ,电子的周期由于运动半径越来越小是 电子的周期由于运动半径越来越小是 连续变化的,所以按卢瑟福的的原子模型辐射 连续变化的,所以按卢瑟福的的原子模型辐射 的电磁波应该是连续谱。 的电磁波应该是连续谱。 3. 经典原子模型的困难 经典原子模型的困难

二、氢原子光谱实验规律 4340.5A 原子光谱是原子内部结构的直接反 映,不同的原子有不同的特征光 4861.3A 谱,定义波数 1 2 6562.8A 任意谱线的波数可以表示为 ==网 n 称为Rydberg公式,R为Rydberg恒量, n、m:正整数 R=1.096776×10m-1 T(m),T(n):光谱项
二、氢原子光谱实验规律 )()() 11 ( ~ 22 nTmT nm ν R −=−= n 、 m:正整数 4 3 4 0.5 Å 原子光谱是原子内部结构的直接反 原子光谱是原子内部结构的直接反 映,不同的原子有不同的特征光 映,不同的原子有不同的特征光 谱,定义波数 17 100967761 − = .R × m nTmT )(),( :光谱项 6562.8 Å 4861.3 Å 任意谱线的波数可以表示为 任意谱线的波数可以表示为 称为Rydberg Rydberg公式 , R 为Rydberg Rydberg恒量 , λ ν ~ 1 =

m取不同值时,给出不同光谱系;n对应于不同谱线 voc)-cT(m)-cT() n>m(n=m+1,m+2,.…) 赖曼系(Lyman)m=1,紫外光 =R0) n=2,3,4
)()() 11 ( ~ 22 ncTmcT nm νν cRc −=−== n>m (n=m+ 1 ,m+2, … ) 赖曼系 (Lyman) m = 1 ,紫外光 ... ,4,3,2 1 1 ~ 1 22 ⎟ = ⎠ ⎞ ⎜ ⎝ ⎛ −= n n ν R m 取不同值时,给出不同光谱系; 取不同值时,给出不同光谱系;n 对应于不同谱线 对应于不同谱线

巴尔末系(Balmer)m=2,可见光 =:) n=3,4,5, 帕邢系(Paschen)m=3,红外光 P=R0)N456
巴尔末系(Balmer) m = 2 , 可见光 ... ,5,4,3 . 1 2 ~ 1 22 ⎟ = ⎠⎞ ⎜⎝⎛ −= n n ν R 帕邢系 (Paschen Paschen) m = 3 , 红外光 ... ,6,5,4 . 1 3 ~ 1 22 ⎟ = ⎠⎞ ⎜⎝⎛ −= n n ν R

三、Bohr理论 Noels Bohr:1922诺贝尔 物理学奖得主 ·1911年赴Cambridge大 学,在Cavendish实验室 工作。 ·1912年在Manchester大学 Rutherford实验室工作四 个月,参加了“粒子散 射实验”研究工作。 ·1913年发表“原子构造和 分子构造”,提出他的氢 和类氢原子结构模型
• 1911 年 赴 Cambridge Cambridge 大 学,在Cavendish Cavendish实验室 工作。 • 1912年在Manchester Manchester大学 Rutherford Rutherford实验室工作四 个月,参加了“α粒子散 射实验”研究工作。 • 1913年发表“原子构造和 分子构造”,提出他的氢 和类氢原子结构模型。 和类氢原子结构模型。 Noels Bohr:1922诺贝尔 物理学奖得主 三、Bohr 理论
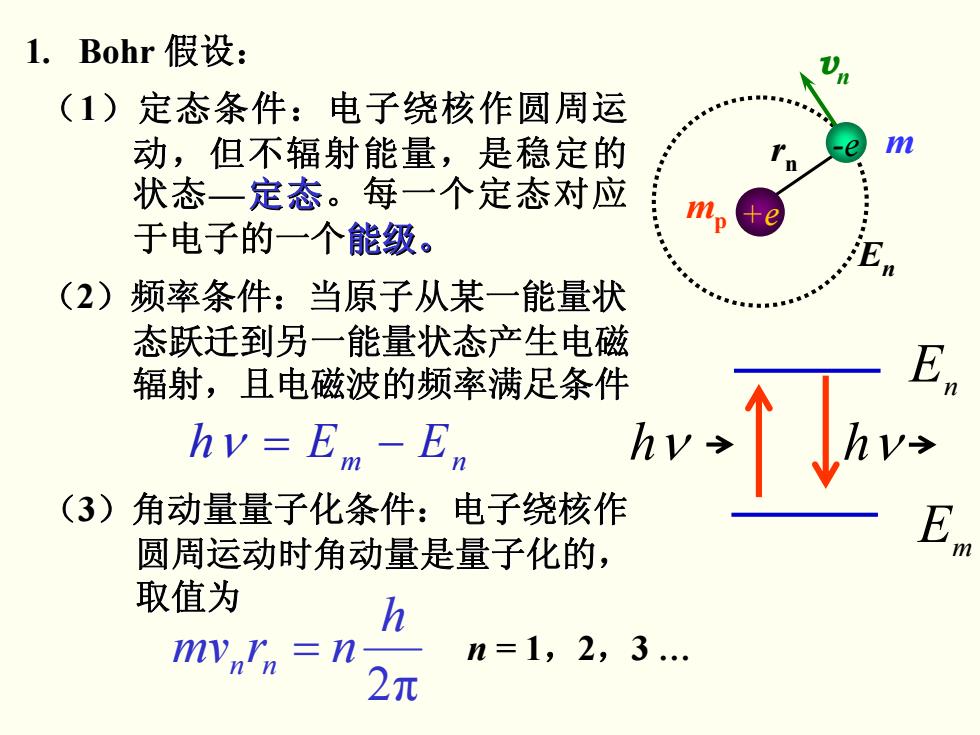
1.Bohr假设: (1)定态条件:电子绕核作圆周运 动,但不辐射能量,是稳定的 状态一定态。每一个定态对应 于电子的一个能级。 me (2)频率条件:当原子从某一能量状 态跃迁到另一能量状态产生电磁 辐射,且电磁波的频率满足条件 hv=Em-En (3)角动量量子化条件:电子绕核作 E 圆周运动时角动量是量子化的, 取值为 h mvarn=n n=1,2,3.. 2元
n = 1,2,3 … (1)定态条件:电子绕核作圆周运 电子绕核作圆周运 动,但不辐射能量,是稳定的 动,但不辐射能量,是稳定的 状态—定态。每一个定态对应 于电子的一个能级。 (2)频率条件:当原子从某一能量状 频率条件:当原子从某一能量状 态跃迁到另一能量状态产生电磁 态跃迁到另一能量状态产生电磁 辐射,且电磁波的频率满足条件 辐射,且电磁波的频率满足条件 ν = − EEh nm (3)角动量量子化条件: 角动量量子化条件:电子绕核作 圆周运动时角动量是量子化的, 角动量是量子化的, 取值为 1. Bohr 假设: hν hν E n E m vn En +e -e m mp rn 2π h nrmv nn =
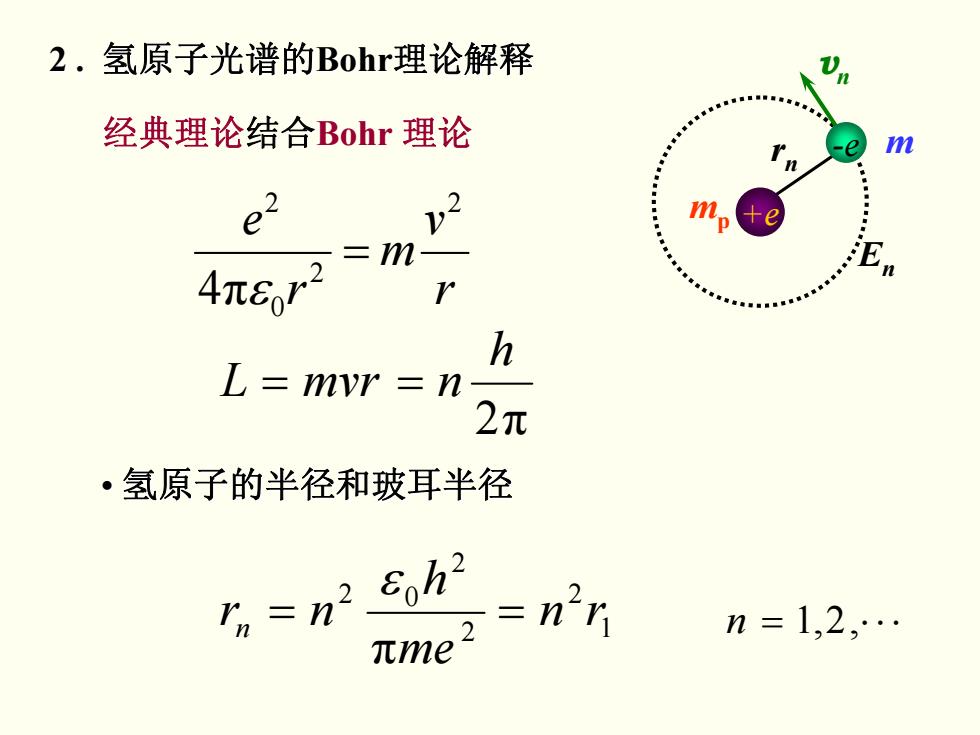
2.氢原子光谱的Bohr理论解释 经典理论结合Bohr理论 e2 =m 4π8r1 h L=mvr =n 2元 ·氢原子的半径和玻耳半径 =n2 8h2 =n'r n=1,2,. 元me1
2 . 氢原子光谱的Bohr理论解释 r v m r e 2 2 0 2 4π = ε 经典理论结合Bohr 理论 • 氢原子的半径和玻耳半径 氢原子的半径和玻耳半径 vn En +e -e m mp rn 2π h == nmvrL 1 2 2 2 2 0 π rn me h nrn = = ε n = ,2,1 ⋅ ⋅ ⋅