
非线性物理:孤波物理 反射势存在时: ·b化,O非零时GLM方程求解就很困难了,解析方法很少,多数用 数值方法和渐近分析方法。这里只是举例说明一些过程。 (I)u(化,0)=-u6y),u>0是常数,8x)是狄拉克函数。 对应u化,0)的薛定谔方程有分立本征值=-k(ku,/2),对应孤波 ;还有>0的连续谱,b(k,0)=u/u。+2i,对应色散波。 最后的解包含两部分:沿x方向传播的孤波和沿-x方向传播的色散 波。孤波对应B在+y,)的求和项,色散波对应于积分项
非线性物理:孤波物理 反射势存在时: • b(k, 0)非零时GLM方程求解就很困难了,解析方法很少,多数用 数值方法和渐近分析方法。这里只是举例说明一些过程。 • (1) u(x, 0)=-u0(x),u0>0是常数, (x) 是狄拉克函数。 • 对应u(x, 0)的薛定谔方程有分立本征值=-k12 (k1=u0/2),对应孤波 ;还有>0的连续谱,b(k, 0)=-u0/(u0+2ik),对应色散波。 • 最后的解包含两部分:沿x方向传播的孤波和沿-x方向传播的色散 波。孤波对应 B(x+y,t) 的求和项,色散波对应于积分项
非线性物理:孤波物理 (a) 0 (b) ·(2)u,0)=-4echx;数值结果如图示。 a (b) (c) -12 -6 12x -12 12x -12 6 12X
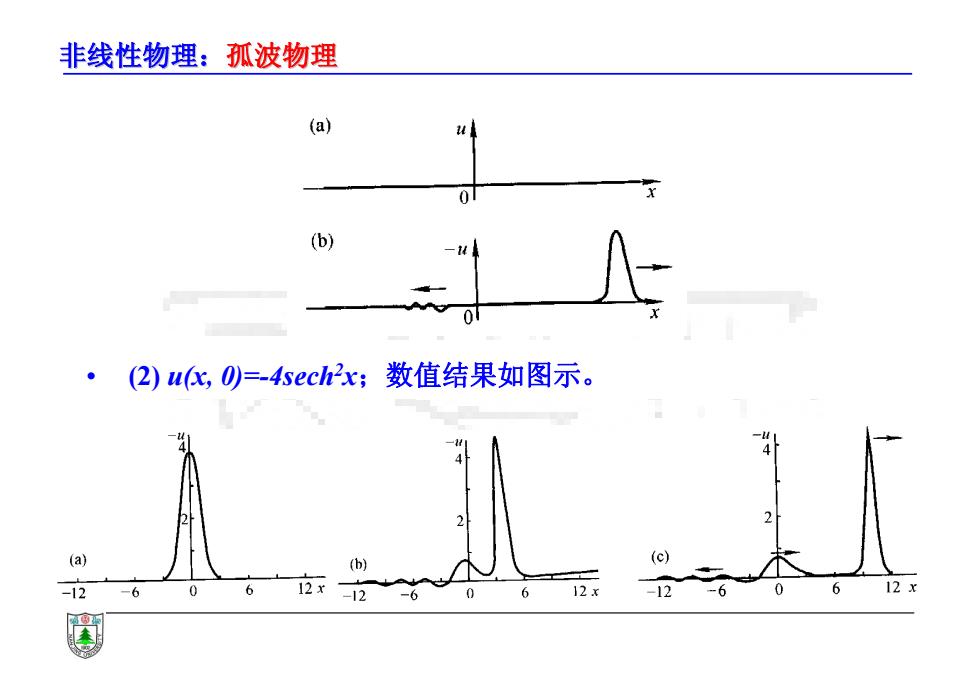
非线性物理:孤波物理 • (2) u(x, 0)=-4sech2x;数值结果如图示
非线性物理:孤波物理 (3)u(:,O=sech2x;数值结果如 图示。 (a) 重要结论:孤波是非线性演化 方程解的一部分,它只依赖于 (b) 相关散射问题的分立本征值。 c
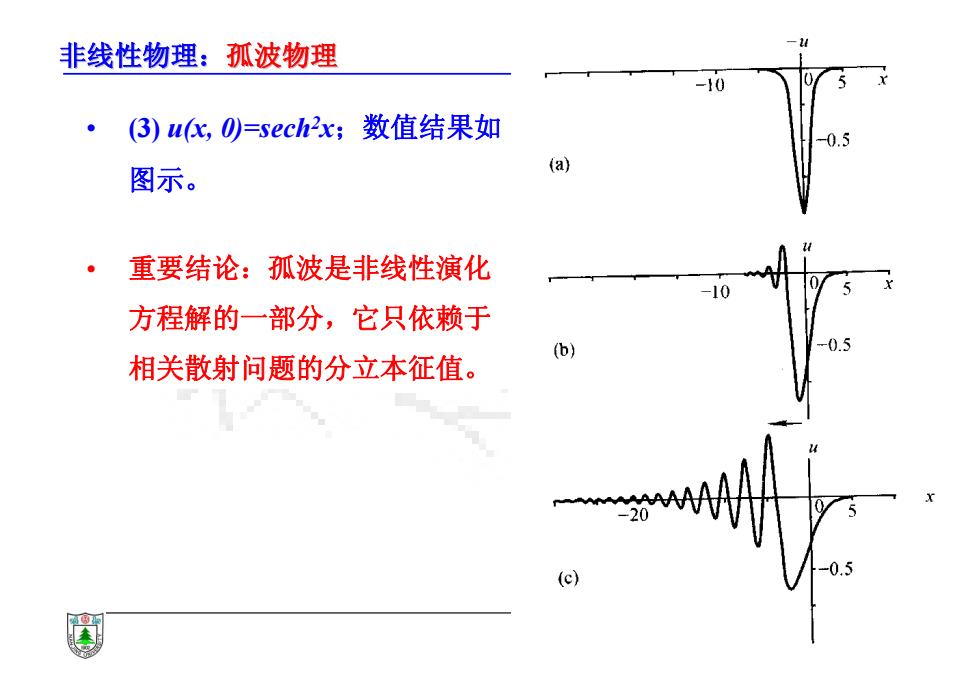
非线性物理:孤波物理 • (3) u(x, 0)=sech2x;数值结果如 图示。 • 重要结论:孤波是非线性演化 方程解的一部分,它只依赖于 相关散射问题的分立本征值

非线性物理:孤波物理 逆散射方法推广: ·Lax方法:1968年Lax将GGKM方法加以推广和标准化,称为Lax 方法。 Zakharovi和Shabat的推广矩阵方法。 AKNS独立的推广矩阵方法。 下面还要介绍一些方法,包括Backlund2变换,Backlund变换与逆 散射方法的关系
非线性物理:孤波物理 逆散射方法推广: • Lax方法:1968年Lax将GGKM方法加以推广和标准化,称为Lax 方法。 • Zakharov和Shabat的推广矩阵方法。 • AKNS独立的推广矩阵方法。 • 下面还要介绍一些方法,包括Backlund变换,Backlund变换与逆 散射方法的关系

非线性物理:孤波物理 Backlund-变换: 考虑如下sine-Gordon方程: uen sinu 。 如果和v都是方程的解,则有下面联立的一阶微分方程组: Ou Ov u+v +2λsin ∂5 05 2 λ≠O,real const. Bu Ov 2 u-V sIn- an an 2 我们称其为sine-Gordon方程的B变换
非线性物理:孤波物理 Backlund变换: • 考虑如下sine-Gordon方程: • 如果u和v都是方程的解,则有下面联立的一阶微分方程组: • 我们称其为sine-Gordon方程的B变换

非线性物理:孤波物理 ·再考虑u和v分别是下面的Burgers?方程和热传导方程的解: 山,+uu=Bx'Y,=Bya ·为正的常数,则下面的一阶微分方程组为B变换: V=-uv/2B y,=(u2-2uv/4B 所以B变换是联系方程两个解的微分方程。功利一些说,如果知 道一个方程的一个解及其B变换,我们可以搞定另外一个解。 这种变换在能够轻易看出一个平庸解的情况下非常有用,因为这 样就可以利用B变换求解另外一个可能很难得到的解
非线性物理:孤波物理 • 再考虑 u 和 v 分别是下面的Burgers方程和热传导方程的解: • 为正的常数,则下面的一阶微分方程组为B变换: • 所以B变换是联系方程两个解的微分方程。功利一些说,如果知 道一个方程的一个解及其B变换,我们可以搞定另外一个解。 • 这种变换在能够轻易看出一个平庸解的情况下非常有用,因为这 样就可以利用B变换求解另外一个可能很难得到的解

非线性物理:孤波物理 ·当然,这种捷径不是那么好看到的,因为对一个方程而言B变换 也不是容易得到的宝贝。Sine-Gordon方程: uen sinu ·显而易见,一个平庸解是=O,利用其B变换得到: Ou L =2入sin 05 2 入≠O,real const. Ou u an 2 各自积分得到:
非线性物理:孤波物理 • 当然,这种捷径不是那么好看到的,因为对一个方程而言B变换 也不是容易得到的宝贝。Sine-Gordon方程: • 显而易见,一个平庸解是v=0,利用其B变换得到: • 各自积分得到:

非线性物理:孤波物理 In[tan(u/4)月=元5+f(n) In[tan(u/4)]=n/2+g() ·f)和g(自分别为针对5和n的积分常数。为了自洽,可以猜出 tan(u/4)的一般形式: tan(u/4)=exp(ag+n/+c) u(5,n)=4tan[exp(5+n/元+c】 ·这个可了不得,它就是sine-Gordon方程的孤子解,真是得来全不 费工夫
非线性物理:孤波物理 • f()和g()分别为针对 和 的积分常数。为了自洽,可以猜出 tan(u/4)的一般形式: • 这个可了不得,它就是sine-Gordon方程的孤子解,真是得来全不 费工夫

非线性物理:孤波物理 关于孤波方程的求解还有微扰方法和数值差分计算方法,限于时 间不再一一介绍,但这些工作依然是目前孤波理论研究的前沿, 同学们可以阅读相关文献
非线性物理:孤波物理 • 关于孤波方程的求解还有微扰方法和数值差分计算方法,限于时 间不再一一介绍,但这些工作依然是目前孤波理论研究的前沿, 同学们可以阅读相关文献

非线性物理:孤波物理 KV方程的守恒律: 我们已经折腾了足够的数学,现在希望稍微物理一点。 ·讨论了这么多KV方程,她有什么值得物理学家爱慕的呢? 有的,因为守恒规律存在于KV方程之中!看到这,物理学家应 该会发疯或者发愤的,虽然只是一字之差。 ·其实就是将孤波看成准粒子啊! 假定p,)是流体密度,v,)是沿x方向的速度,质量演化满足: ap a(pv)=0 pw→c0nst.ifx→0 8t Ox
非线性物理:孤波物理 KdV方程的守恒律: • 我们已经折腾了足够的数学,现在希望稍微物理一点。 • 讨论了这么多KdV方程,她有什么值得物理学家爱慕的呢? • 有的,因为守恒规律存在于KdV方程之中!看到这,物理学家应 该会发疯或者发愤的,虽然只是一字之差。 • 其实就是将孤波看成准粒子啊! • 假定(x,t)是流体密度,v(x,t)是沿 x方向的速度,质量演化满足: