
非线性物理:基础知识一一相空间 单摆问题: ·无阻尼单摆例子,哈密顿H为: H=K+V=2/2+0 cosx,p=-0H/0q,q=0H /op x angle &@o=int rinsic frequency,p=x,q=x 0 ·无阻尼单摆例子,运动方程为: 8=x %,=0→+isinx=0 mg
非线性物理:基础知识--相空间 基础知识--相空间 单摆问题: • 无阻尼单摆例子,哈密顿H为: x angle & int rinsic frequency, p x,q x H K V x / 2 cos x, p H / q, q H / p 0 2 0 2 • 无阻尼单摆例子,运动方程为: 0 x sin x 0 t H 2 0 = x

非线性物理:基础知识一一相空间 ·平衡位置: x。=0,x。=nπ(n=0,±1,±2,) 系统势能在一个固定范围内交替变化: V(x)=-0)C0sx→ Vmn=-oi,e=nπ(n≥0) 'na=o,x。=nπ(n≤0)
非线性物理:基础知识--相空间 基础知识--相空间 • 平衡位置: • 系统势能在一个固定范围内交替变化: x 0, x n ( n 0, 1, 2,...) e e V , x n ( n 0 ) V , x n ( n 0 ) V( x ) cos x e 2 max 0 e 2 2 min 0 0
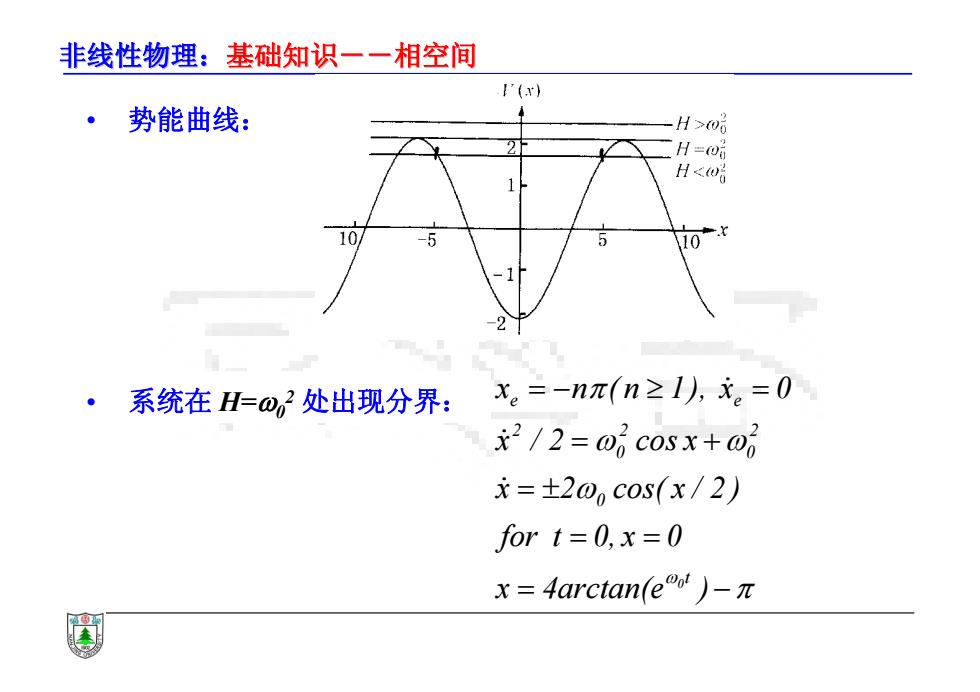
非线性物理:基础知识一一相空间 '(r) ·势能曲线: H>0 H=O品 H<w号 -5 10*t ·系统在H=o,2处出现分界: x。=-nπ(n≥l,x。=0 2/2=0pcosx+0b x=±20c0s(x/2) for t=0,x=0 x=4 arctan(eo')-π
非线性物理:基础知识--相空间 基础知识--相空间 • 势能曲线: • 系统在 H=02 处出现分界: x 4arctan(e ) for t 0, x 0 x 2 cos( x / 2 ) x / 2 cos x x n ( n 1), x 0 t 0 2 0 2 0 2 e e 0

非线性物理:基础知识一一相空间 分界线将系统动力学分成单摆与圆周运动两个区域:H0,时,圆周运动。 ·摆动初始位置x→π,摆动周期越长,除非给定初速:o
非线性物理:基础知识--相空间 基础知识--相空间 • 分界线将系统动力学分成单摆与圆周运动两个区域: H02 时,圆周运动。 • 摆动初始位置 x0,摆动周期越长,除非给定初速:H>02
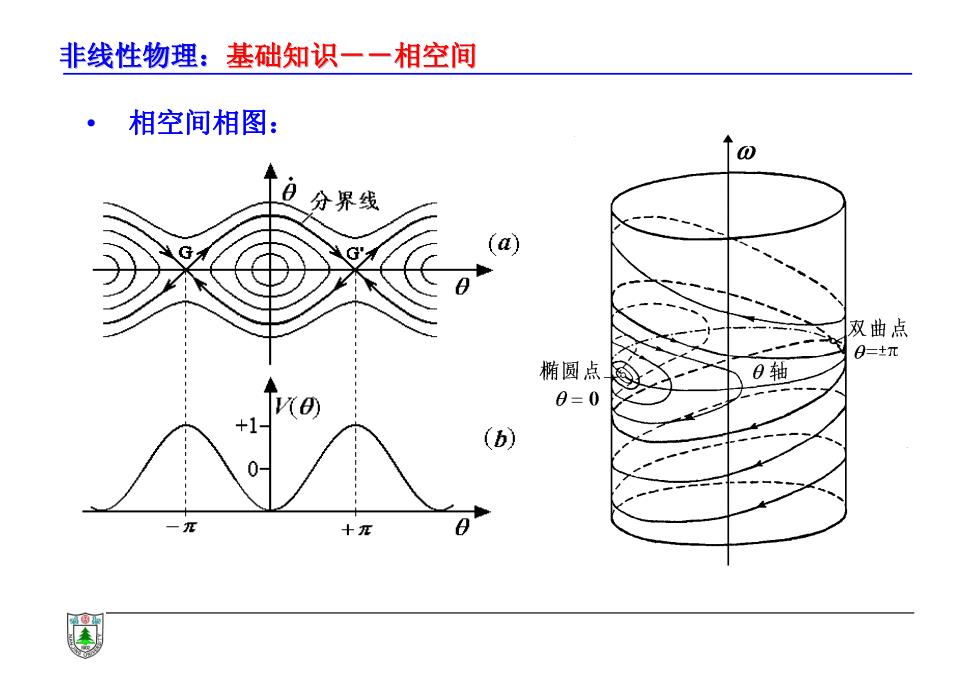
非线性物理:基础知识一一相空间 ·相空间相图: 0 日分界线 (a) 双曲点 0=±元 椭圆点 0轴 0=0 (b) 0 十π
非线性物理:基础知识--相空间 基础知识--相空间 • 相空间相图:

非线性物理:基础知识一一相空间 ·对于分界线性质,可求解分界方程看摆动速度与时间的关系: 2tanx .sin 2x=- .∴.C0S 一三 (1+tan'x) 2 cosh(@t) x=4 arctan(e)-元i=vft)=± 200 cosh(@t)
非线性物理:基础知识--相空间 基础知识--相空间 • 对于分界线性质,可求解分界方程看摆动速度与时间的关系: cosh( t ) 2 x 4arctan(e ) x v(t ) cosh( t ) 1 2 x cos (1 tan x ) 2tan x sin 2x 0 t 0 0 2 0
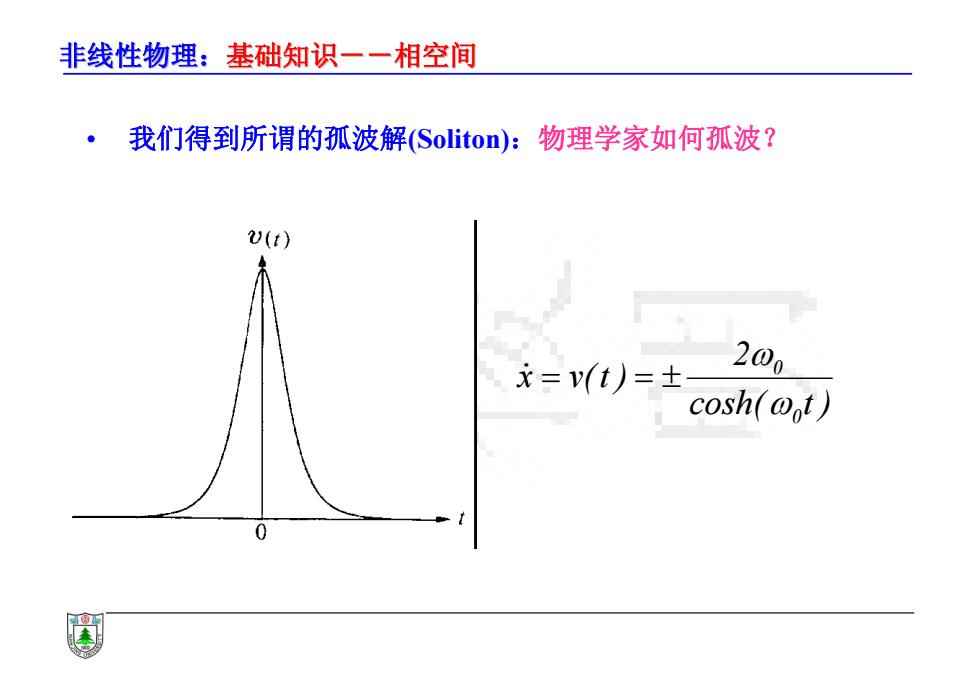
非线性物理:基础知识一一相空间 ·我们得到所谓的孤波解(Soliton): 物理学家如何孤波? 0(t) 200 。 术=1)=± cosh(ot)
非线性物理:基础知识--相空间 基础知识--相空间 • 我们得到所谓的孤波解(Soliton):物理学家如何孤波? cosh( t ) 2 x v(t ) 0 0

非线性物理:基础知识一一相空间 ·当单摆存在阻尼时: 0+2B0+o0=0 2+2B1+o=0 元2=-B±VB2-o8 0=Vo6-B2 入12=-B±i0 0=P.e cos(ot+p) 0=-P.e[Bcos(@t+p)+osin(@t+p)]
非线性物理:基础知识--相空间 基础知识--相空间 • 当单摆存在阻尼时: 2 0 2 0 2 0 20 2 2 0 2 1,2 2 2 0 1,2 i cos( ) P e t [ cos( ) sin( )] P e t t t
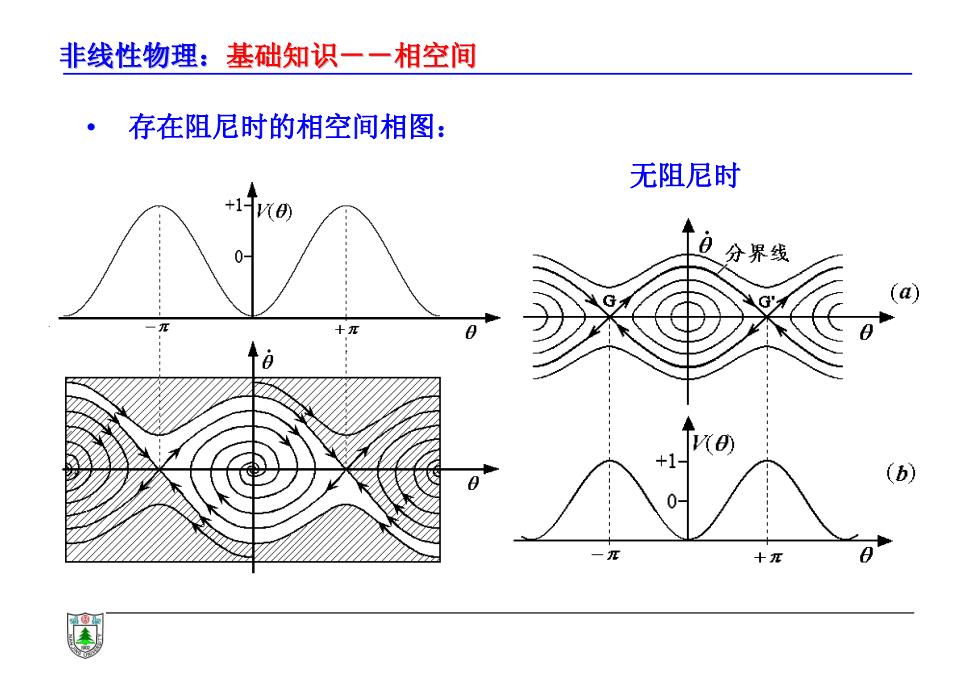
非线性物理:基础知识一一相空间 ·存在阻尼时的相空间相图: 无阻尼时 、分界线 a +1 (b)
非线性物理:基础知识--相空间 基础知识--相空间 • 存在阻尼时的相空间相图: 无阻尼时

非线性物理:基础知识一一相空间 相空间: 绝大多数非线性问题要么找不到描述的微分方程,要么微分方 程无解。建立空间几何分析图像比较有效。 ·动力学系统满足牛顿力学: 龙=F v=x(t) ·用位置x)和速度v就可以完全描述系统状态,用平面c,以上 的点表示这个状态,即化)空间是相空间
非线性物理:基础知识--相空间 基础知识--相空间 相空间: • 绝大多数非线性问题要么找不到描述的微分方程,要么微分方 程无解。建立空间几何分析图像比较有效。 • 动力学系统满足牛顿力学: • 用位置 x(t) 和速度 v 就可以完全描述系统状态,用平面(x,y)上 的点表示这个状态,即(x,y)空间是相空间