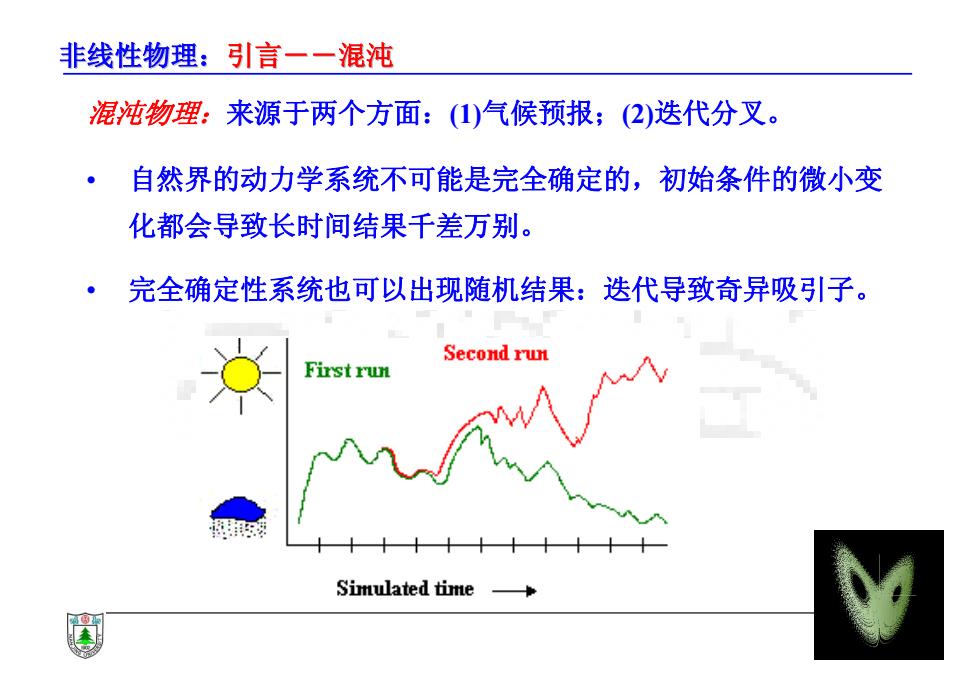
非线性物理:引言一一混沌 混沌物理:来源于两个方面:(1)气候预报;(2)迭代分叉。 自然界的动力学系统不可能是完全确定的,初始条件的微小变 化都会导致长时间结果千差万别。 完全确定性系统也可以出现随机结果:迭代导致奇异吸引子。 Second run First run 十 Simulated time
非线性物理:引言--混沌 混沌物理:来源于两个方面:(1)气候预报;(2)迭代分叉。 • 自然界的动力学系统不可能是完全确定的,初始条件的微小变 化都会导致长时间结果千差万别。 • 完全确定性系统也可以出现随机结果:迭代导致奇异吸引子
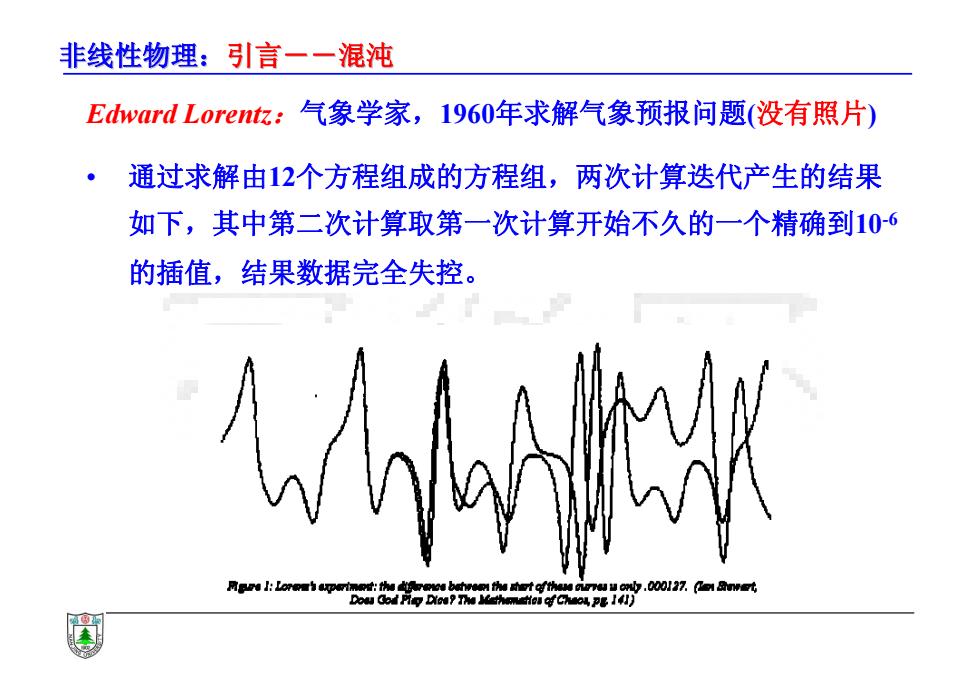
非线性物理:引言一一混沌 Edward Lorent:气象学家,1960年求解气象预报问题(没有照片) 通过求解由12个方程组成的方程组,两次计算迭代产生的结果 如下,其中第二次计算取第一次计算开始不久的一个精确到106 的插值,结果数据完全失控。 1 Te u on.Co0l77.nnw式
非线性物理:引言--混沌 Edward Lorentz:气象学家,1960年求解气象预报问题(没有照片) • 通过求解由12个方程组成的方程组,两次计算迭代产生的结果 如下,其中第二次计算取第一次计算开始不久的一个精确到10-6 的插值,结果数据完全失控

非线性物理:引言一一混沌 迭代问题 Strange attractor from Lorentz: dx/dt=a(y-x) dy/dt=x(b-z)-y d7/dt=xy-cz
非线性物理:引言--混沌 Strange attractor from Lorentz: dx/dt=a(y-x) dy/dt=x(b-z)-y dz/dt=xy-cz 迭代问题

非线性物理:引言一一混沌 混沌散射 1.一个晶格粒子按照如下势能 函数进行散射: 2. V=(2)*6y2)*xp 2+y2/ 3. 颜色深浅表示所在位置粒子 被散射前停留的时间分布。 4. 停留时间分布具有奇异吸引 子特征和分形特征。 福
非线性物理:引言--混沌 混沌散射 1. 一个晶格粒子按照如下势能 函数进行散射: 2. V(x,y)=(x^2)*(y^2)*exp[- (x^2+y^2)] 3. 颜色深浅表示所在位置粒子 被散射前停留的时间分布。 4. 停留时间分布具有奇异吸引 子特征和分形特征

非线性物理:引言一一混沌 Ikeda Attractor zn+i=a+bz explik -ip/(1+2 =0.85,b=0.9,k=0.4,p=7.7 The pictures here show the strange attractor that results from the time evolution of an optical cavity containing a nonlinear dielectric subjected to a periodic string of light pulses.The picture is a cumulative plot of the phase and amplitude 4 of the pulse.For a given output pulse the complex number Z=Aexp(i)is obtained (Re(Z)=horizontal axis and Im(Z)=vertical axis).Pixel colors are plotted according to how often Z falls onto that pixel. ®
非线性物理:引言--混沌 The pictures here show the strange attractor that results from the time evolution of an optical cavity containing a nonlinear dielectric subjected to a periodic string of light pulses. The picture is a cumulative plot of the phase and amplitude A of the pulse. For a given output pulse the complex number Z=Aexp(i) is obtained (Re(Z)=horizontal axis and Im(Z)=vertical axis). Pixel colors are plotted according to how often Z falls onto that pixel. Ikeda Attractor zn+1=a+bznexp[ik -ip/(1+|zn2|)] a=0.85, b=0.9, k=0.4, p=7.7

非线性物理:引言一一混沌 Ikeda Attractor n+=a+bz explik -ip/(1+20 =0.85,b=0.9,k=0.4,p=7.7 The bright yellow signifies high density,often visited region and the red region signifies low density, rarely visited region of the attractor.The two pictures are set at different parameter values and this picture is also "zoomed in"of the previous one
非线性物理:引言--混沌 Ikeda Attractor zn+1=a+bznexp[ik -ip/(1+|zn2|)] a=0.85, b=0.9, k=0.4, p=7.7 The bright yellow signifies high density, often visited region and the red region signifies low density, rarely visited region of the attractor. The two pictures are set at different parameter values and this picture is also "zoomed in“ of the previous one

非线性物理:引言一一混沌 KAM(Kolmogorov 1954,Arnold 1963a,Moser 1963)islands This is probably a picture of the Standard map which is a Hamiltonian (conservative)system.An obvious feature of the picture is the KAM islands
非线性物理:引言--混沌 KAM (Kolmogorov 1954, Arnold 1963a, Moser 1963) islands This is probably a picture of the Standard map which is a Hamiltonian (conservative) system. An obvious feature of the picture is the KAM islands

非线性物理:引言一一混沌 x+xn2-yn2+0.9gn+0.6013yn yn+I=2xnVn-2xn+0.5ym Tinkerbell Attractor The Tinkerbell attractor is represented by the curve and its basin of attraction is represented by the black color.Other colors denote points which escape to infinity as one continually iterates the two-dimensional map.The colors are shaded according to how fast the points escapes to infinity
非线性物理:引言--混沌 Tinkerbell Attractor The Tinkerbell attractor is represented by the curve and its basin of attraction is represented by the black color. Other colors denote points which escape to infinity as one continually iterates the two-dimensional map. The colors are shaded according to how fast the points escapes to infinity. xn+1=xn2-yn2+0.9xn+0.6013yn yn+1=2xnyn-2xn+0.5yn

非线性物理:引言一一混沌 红、黄Forced Damped Pendulum 绿、蓝 ..with Four Basins Even something as simple as a periodically forced damped pendulum can have complex behavior.The computer-generated images left show initial positions that asymptote to one of different behaviors (one color for each behavior). For example,orbits starting at points in the blue region would yield a different type of motion from X"(t)+a*X(t)+sinX(t) orbits starting in the red region.The brighter the =F) shade of color,the longer it takes to settle into the F(t)=b+c*cos(t) corresponding motion.The different regions are separated by fractal basin boundaries.The pictures are made at increasing magnification levels
非线性物理:引言--混沌 红、黄 Forced Damped Pendulum 绿、蓝 ...with Four Basins Even something as simple as a periodically forced damped pendulum can have complex behavior. The computer-generated images left show initial positions that asymptote to one of different behaviors (one color for each behavior). For example, orbits starting at points in the blue region would yield a different type of motion from orbits starting in the red region. The brighter the shade of color, the longer it takes to settle into the corresponding motion. The different regions are separated by fractal basin boundaries. The pictures are made at increasing magnification levels. X''(t)+a*X'(t)+sinX(t) =F(t) F(t)=b+c*cos(t)

非线性物理:引言一一混沌
非线性物理:引言--混沌