
非线性物理:形态发生 扩散限制系统生长:微观模型 ·模拟生长过程的形态发生,微观上可以利用原子聚集机理,而宏 观上采用扩散方程和界面毛细张力的耦合求解。 ·微观模型的主要优点是通过改变微观机制可以很方便地模拟晶体 生长的各种过程,包括成核、生长、熔化、扩散等等,缺点是不 能给出宏观实验可测的一些物理量,如界面张力,晶体各向异性 等。而且微观模型中噪声不可避免。 ·上述一些缺点在宏观连续模型中可以避免,但是宏观模型的严格 求解变得十分困难,甚至不可能。 ·我们从微观分形开始
非线性物理:形态发生 扩散限制系统生长:微观模型 • 模拟生长过程的形态发生,微观上可以利用原子聚集机理,而宏 观上采用扩散方程和界面毛细张力的耦合求解。 • 微观模型的主要优点是通过改变微观机制可以很方便地模拟晶体 生长的各种过程,包括成核、生长、熔化、扩散等等,缺点是不 能给出宏观实验可测的一些物理量,如界面张力,晶体各向异性 等。而且微观模型中噪声不可避免。 • 上述一些缺点在宏观连续模型中可以避免,但是宏观模型的严格 求解变得十分困难,甚至不可能。 • 我们从微观分形开始

非线性物理:形态发生 DBM模型:噪声与尖端分叉 ·这里DBM称之为dense branching model,基于DLA。 ·这里考虑的DLA是包括界面毛细张力和噪声抑制下的DLA,主 要是为了证明DLA机制适合于模拟实际的晶体生长形态和速率 选择机制,虽然问题远没有进展。AA ·先看Nittmann和Stanley:关于噪声抑制效应的工作。这一工作源 于实际系统中两类不同的生长机理:枝晶生长和尖端分叉
非线性物理:形态发生 DBM模型:噪声与尖端分叉 • 这里DBM称之为dense branching model,基于DLA。 • 这里考虑的DLA是包括界面毛细张力和噪声抑制下的DLA,主 要是为了证明DLA机制适合于模拟实际的晶体生长形态和速率 选择机制,虽然问题远没有进展。^_^ • 先看Nittmann和Stanley关于噪声抑制效应的工作。这一工作源 于实际系统中两类不同的生长机理:枝晶生长和尖端分叉
非线性物理:形态发生 e. 72 f, 2 6帆牌兰P观M v=80 v=100
非线性物理:形态发生

非线性物理:形态发生 wiin mAAAAns Flg.3.Hele-Shaw experiment in which the inviscid fluid enters through a central orifice and forms fingers that move radially outward.One of these fingers has trapped a small bubble at its tip.As a result,it is growing stably at constant speed and is emitting sidebranches.(Photograph courtesy of Y. Couder.)
非线性物理:形态发生

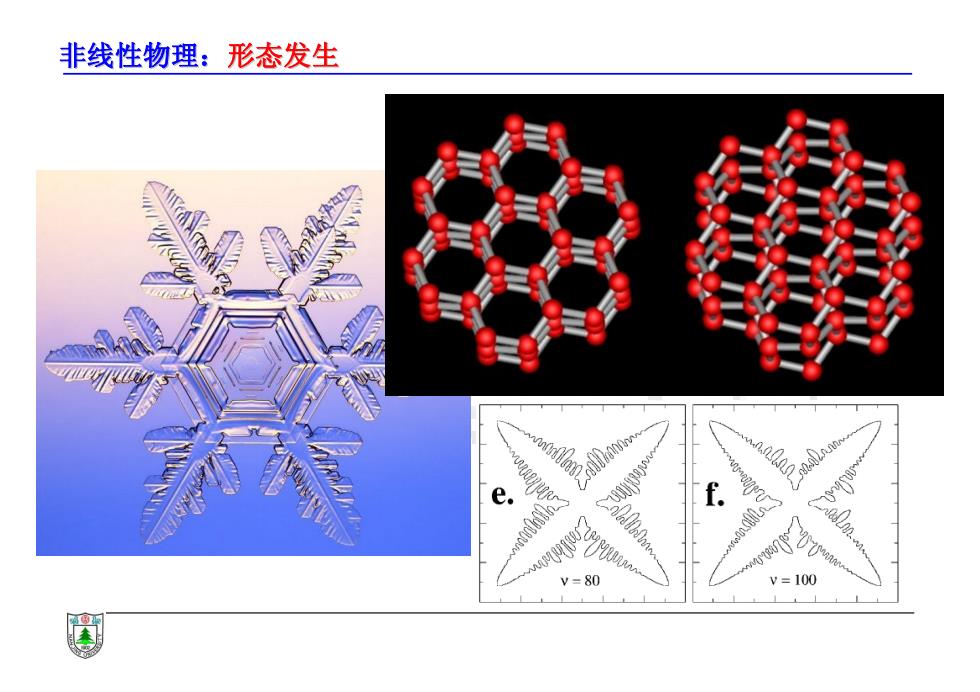
非线性物理:形态发生 枝晶生长关键的科学问题是由于什么机制使得非常微弱的水分子 排列各向异性能够充分发大到宏观的雪花层次: ·三岁孩儿都知道什么是雪花,什么是电影中的棉花 ·对于尖端分叉,以粘性指为例。两种液体界面形态没有什么各向 异性对称性,但尖端分叉不断发生,原因可以理解成两者界面张 力导致一个特征尺度的存在,从而出现尖端分叉。 ·但是如果两液体互溶,那就没有界面张力,但分叉仍然会发生。 问题出现了:是什么因素导致尖端分叉的发生?
非线性物理:形态发生 • 枝晶生长关键的科学问题是由于什么机制使得非常微弱的水分子 排列各向异性能够充分发大到宏观的雪花层次: • 三岁孩儿都知道什么是雪花,什么是电影中的棉花^_^ • 对于尖端分叉,以粘性指为例。两种液体界面形态没有什么各向 异性对称性,但尖端分叉不断发生,原因可以理解成两者界面张 力导致一个特征尺度的存在,从而出现尖端分叉。 • 但是如果两液体互溶,那就没有界面张力,但分叉仍然会发生。 问题出现了:是什么因素导致尖端分叉的发生?

非线性物理:形态发生 上述两种生长形态的差异一直被认为源于不同的物理机制,其实 它们之间可以统一。从微观上描述这种统一模型的初步工作应该 得到关注。^ ·从简化的模拟粘性指的DBM模型开始:根据Laplace方程确定一 个集团周边位置下一次被占据的概率,然后进行选择性生长。因 为每一次生长只是由一个随机数来决定,因此微观上系统存在很 大的噪声。 ·宏观上,DBM界面生长是与界面位置的压力梯度成比例的,这 个类似于流体的Darcy定律: v=-n.VP
非线性物理:形态发生 • 上述两种生长形态的差异一直被认为源于不同的物理机制,其实 它们之间可以统一。从微观上描述这种统一模型的初步工作应该 得到关注。^_^ • 从简化的模拟粘性指的DBM模型开始:根据Laplace方程确定一 个集团周边位置下一次被占据的概率,然后进行选择性生长。因 为每一次生长只是由一个随机数来决定,因此微观上系统存在很 大的噪声。 • 宏观上,DBM界面生长是与界面位置的压力梯度成比例的,这 个类似于流体的Darcy定律:

非线性物理:形态发生 ·为了抑制微观噪声,采取的机制是:一个界面位置除非被选择生 长s次,否则不允生长。从而引入了s这个可调控参数。 ·当s为无穷,即所谓零噪声态,界面生长严格满足Darcy定律了。 ·下页三个图分别对应于s=2,s=20和s=200的情况。图b和图c的形 态与牛顿流体与非牛顿流体构成的粘性指尖端分叉形态相像。 S=2时,所得形态是标准的DBM,d1.7。当s很大时,所得形态 似乎是新的普适类,但在很大尺度上求其分形维,发现d=1.7仍 然成立,即生长形态是相同的,与噪声抑制因子s无关。 尖端分叉机制:随着一个尖端生长,曲率半径增大,然后尖端开 始粗糙化,出现涨落
非线性物理:形态发生 • 为了抑制微观噪声,采取的机制是:一个界面位置除非被选择生 长s次,否则不允生长。从而引入了s这个可调控参数。 • 当s为无穷,即所谓零噪声态,界面生长严格满足Darcy定律了。 • 下页三个图分别对应于s=2, s=20和s=200的情况。图b和图c的形 态与牛顿流体与非牛顿流体构成的粘性指尖端分叉形态相像。 s=2时,所得形态是标准的DBM,df=1.7。当s很大时,所得形态 似乎是新的普适类,但在很大尺度上求其分形维,发现df=1.7仍 然成立,即生长形态是相同的,与噪声抑制因子s无关。 • 尖端分叉机制:随着一个尖端生长,曲率半径增大,然后尖端开 始粗糙化,出现涨落

非线性物理:形态发生 s=20 s=2
非线性物理:形态发生 s=2 s=20

非线性物理:形态发生 s=200
非线性物理:形态发生 s=200

非线性物理:形态发生 ·沿生长法向的涨落很快消失,而沿生长负方向的涨落出现进一步 发展,原因在于屏蔽效应。 。 每一个枝叉的宽度与噪声抑制因子s的关系大致满足:W一 4.510gs+2,与压力梯度无关。 ·上述模型虽然在宏观上被解释为界面张力效应,但是在微观模型 上实际上没有引入任何界面张力,这一点我们在前面关于DLA 章节中已经讨论过。因此,微观上导致形态发生变化的只是噪声 被抑制。这是强调噪声对形态发生有巨大影响的强有力例子
非线性物理:形态发生 • 沿生长法向的涨落很快消失,而沿生长负方向的涨落出现进一步 发展,原因在于屏蔽效应。 • 每一个枝叉的宽度与噪声抑制因子s的关系大致满足:Wf ~ 4.5logs+2,与压力梯度无关。 • 上述模型虽然在宏观上被解释为界面张力效应,但是在微观模型 上实际上没有引入任何界面张力,这一点我们在前面关于DLA 章节中已经讨论过。因此,微观上导致形态发生变化的只是噪声 被抑制。这是强调噪声对形态发生有巨大影响的强有力例子