
非线性物理:分形物理 生长问题: 自然界有很多物质形态,象Gold Black,coagulated aerosols等等 都是颗粒聚集呈现非常纤细的形态。 ·这些聚集体的空间相关函数与尺度都呈幂指数关系,其形成过程 具有强烈的动力学特征。 与此类似的平衡结构有Eden growth model生长模型,random animals随机动物,self-avoiding walk自规避行走和percolating clusters渗流集团。 前者是动力学结构,后者是平衡结构
非线性物理:分形物理 生长问题: • 自然界有很多物质形态,象Gold Black,coagulated aerosols等等 都是颗粒聚集呈现非常纤细的形态。 • 这些聚集体的空间相关函数与尺度都呈幂指数关系,其形成过程 具有强烈的动力学特征。 • 与此类似的平衡结构有Eden growth model生长模型,random animals随机动物,self-avoiding walk自规避行走和percolating clusters渗流集团。 • 前者是动力学结构,后者是平衡结构

非线性物理:分形物理 DLA模型: DLA模型是Eden模型的另一个变种,其主要差别是加进了动力学 效应:颗粒不是随机加在已存在颗粒周围,而是通过从远处随机 扩散来实现sticking,进而生长。 ·具有随机扩散的动力学会变得十分不同!扩散拉普拉斯方程! ()加入了动力学行为后形成的结构有什么特征? (2)宏观描述背后的微观机理是什么? 3)如何与非线性动力学联系起来?
非线性物理:分形物理 DLA模型: • DLA模型是Eden模型的另一个变种,其主要差别是加进了动力学 效应:颗粒不是随机加在已存在颗粒周围,而是通过从远处随机 扩散来实现sticking,进而生长。 • 具有随机扩散的动力学会变得十分不同!扩散拉普拉斯方程! • (1) 加入了动力学行为后形成的结构有什么特征? • (2) 宏观描述背后的微观机理是什么? • (3) 如何与非线性动力学联系起来?

非线性物理:分形物理 DLA模型基本步骤如下: ()点阵原点存在一个颗粒; (2)第二个粒子从远处某个随机位置发出,空间进行随机行走,直 到碰上一个已存在的颗粒,则此颗粒固定下来。 (3)重复过程(1)和(2)。 (4)如果颗粒碰上边界,此颗粒被舍弃。 。 这种生长一个突出的特点是越是向外伸展的聚集体枝叉生长得越 快,即所谓“shadowed'效应,因此聚集体比Eden模型要开放
非线性物理:分形物理 • DLA模型基本步骤如下: • (1)点阵原点存在一个颗粒; • (2)第二个粒子从远处某个随机位置发出,空间进行随机行走,直 到碰上一个已存在的颗粒,则此颗粒固定下来。 • (3)重复过程(1)和(2)。 • (4)如果颗粒碰上边界,此颗粒被舍弃。 • 这种生长一个突出的特点是越是向外伸展的聚集体枝叉生长得越 快,即所谓“shadowed”效应,因此聚集体比Eden模型要开放

非线性物理:分形物理 20 Lattice Constants
非线性物理:分形物理

非线性物理:分形物理 相关性分析:上图是一个典型的正方点阵模拟的DLA cluster,在 三角点阵或者无规点阵里面一样。 ·结构分析手段之一是空间相关函数。聚集体密度的定义是: p()=l if occupied p(r)=0 if not yet 一个含N个颗粒的聚集体相关函数定义如下,这个定义只是对系 综平均相关函数的近似表达 c6r)=N2pp6r'+r, (p()p('+》/八p()》
非线性物理:分形物理 • 相关性分析:上图是一个典型的正方点阵模拟的DLA cluster,在 三角点阵或者无规点阵里面一样。 • 结构分析手段之一是空间相关函数。聚集体密度的定义是: (r) 0 if not yet (r ) 1if occupied • 一个含N个颗粒的聚集体相关函数定义如下,这个定义只是对系 综平均相关函数的近似表达
非线性物理:分形物理 只要远小于聚集体尺度,上述 相关函数应该只与距离相关。 .2 043r034 。 对上图DLA聚集体的分析计算 C(r) 15 得到相关函数如右图所示,数 据是对六个3000颗粒的 10 aggregates沿各个方向统计平均 的结果。 2.0 5.0 10.0 20.0 50.0 r(Lattice Const)
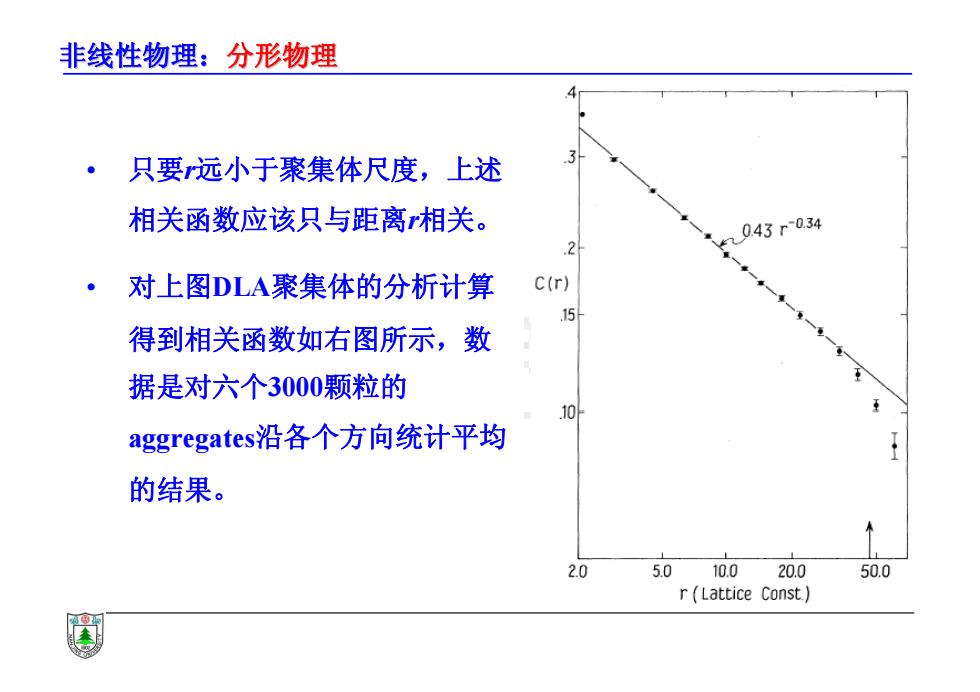
非线性物理:分形物理 • 只要r远小于聚集体尺度,上述 相关函数应该只与距离r相关。 • 对上图DLA聚集体的分析计算 得到相关函数如右图所示,数 据是对六个3000颗粒的 aggregates沿各个方向统计平均 的结果

非线性物理:分形物理 TABLE I.Values of the correlation exponent A for diffusion-limited aggregation model and other systems. 重要的是幂指数 A Two Three 相关性。 dimensions dimensions Diffusion-limited aggregation: Square lattice,average of six clusters of 对三角点阵有类 2079-3609 particles in size (Fig.2). 0.343±0.004a Triangular lattice,average of three clusters of 1500-2997 particles. 0.327±0.01 似的幂指数结果 Radius of gyration,weighted average of A values inferred for six clusters of 999-3000 particle8,Eq.⑤). 0.299±0.02 Koch curve with A =2D =0.416,measured average correlation function of seven curves. translated and rotated at random. 0.42 ·其它结果总结在 Metal-particle aggregates correlations of particle density from micrographs,Ref.3. 0.32±0.01b 1.320.019 表I中。 Self-avoiding walk (flight), correlations of step density,Ref.6. 0.667 1.33 Percolation,from radius of gyration of clusters at threshold,Eq.(5), C6y)~r0.343趾0.004, Refs.5 and 7. ≈0.2 0.9 Random animals from radius of gyration, Eq.(5),Ref.5. 0.46 1.18
非线性物理:分形物理 • 重要的是幂指数 相关性。 • 对三角点阵有类 似的幂指数结果 。 • 其它结果总结在 表 I 中

非线性物理:分形物理 分形分析:DLA所给予我们直观的分形特征指导我们进行分形分 析。先从数学上和Koch结构开始。 利用上面的空间相关函数方法进行分析得出幂指数为-0.42,而 Koch结构的分形维严格上是D=n3/Mn2=1.585=2.0-0.42。 ·在Hausdorff集合中密度相关具有如下形式: (p(p(+)》~rD-d=rA. ·可以理解,一个开放的体系空间相关性总是随着距离而衰减的。 我们来看看如何推出这一关系
非线性物理:分形物理 • 分形分析:DLA所给予我们直观的分形特征指导我们进行分形分 析。先从数学上和Koch结构开始。 • 利用上面的空间相关函数方法进行分析得出幂指数为-0.42,而 Koch结构的分形维严格上是D=ln3/ln2=1.585=2.0-0.42。 • 在 Hausdorff 集合中密度相关具有如下形式: • 可以理解,一个开放的体系空间相关性总是随着距离而衰减的。 我们来看看如何推出这一关系

非线性物理:分形物理 所谓Hausdorff集是指这样一个空间,它可以被半径为a的物体 填充,但拓扑学上看并没有填满。而半径为α的物体个数K(@)按 照D变化。这是我们前面讲分形维定义时已经讲到。 这样空间体积为V=K(D。而每一个物体的平均体积 N(~1K(o~P。按照空间相关函数的定义,我们有: aP-Nla)=∫2rXp(》roccuped =ar(p()p(o》/八p(0》, (p()p(+)》心rD-d=rA
非线性物理:分形物理 • 所谓 Hausdorff 集是指这样一个空间,它可以被半径为 a 的物体 填充,但拓扑学上看并没有填满。而半径为 a 的物体个数 K(a) 按 照 a-D 变化。这是我们前面讲分形维定义时已经讲到。 • 这样空间体积为 V=K(a)ad~ad-D。而每一个物体的平均体积 N(a)~1/K(a)~aD。按照空间相关函数的定义,我们有:

非线性物理:分形物理 这里是空间维数。可以看出,要满足上式,相关函数必须是第 二行的形式,因为将相关函数表达式代入上式就得到N(@)~P。 ·记住:不要管系数的变化,只管幂指数的变化。 在很大或者很小时,相关函数对幂指数律的偏离是因为存在一个 下限尺度和上限尺度。 ·当然,更为直接的是颗粒数目N对聚集体回转尺寸R的幂指数律关 系: N(a)~a°for asR, N~RD=R4-A
非线性物理:分形物理 • 这里d是空间维数。可以看出,要满足上式,相关函数必须是第 二行的形式,因为将相关函数表达式代入上式就得到N(a)~aD。 • 记住:不要管系数的变化,只管幂指数的变化。 • 在r很大或者很小时,相关函数对幂指数律的偏离是因为存在一个 下限尺度和上限尺度。 • 当然,更为直接的是颗粒数目N对聚集体回转尺寸R的幂指数律关 系: