
非线性物理:基础知识一一相空间 庞加莱映射: 。 相空间轨道方法是庞加莱建立,但是轨道形态仍然很复杂,这导 致他提出庞加莱截面的概念。 ·在相空间取某一坐标为常数的截面,将相空间的轨迹演化简化成 轨迹线与这一截面的交点在截面上的运动一一缩小了一维! 设相空间是n维的,原则上可以取出一个(n-1)维相平面,称为庞 加莱截面。 将这种时间上连续的运动转变为离散的图象处理方法称为庞加莱 映射
非线性物理:基础知识--相空间 基础知识--相空间 庞加莱映射: • 相空间轨道方法是庞加莱建立,但是轨道形态仍然很复杂,这导 致他提出庞加莱截面的概念。 • 在相空间取某一坐标为常数的截面,将相空间的轨迹演化简化成 轨迹线与这一截面的交点在截面上的运动--缩小了一维! • 设相空间是n维的,原则上可以取出一个(n-1)维相平面,称为庞 加莱截面。 • 将这种时间上连续的运动转变为离散的图象处理方法称为庞加莱 映射
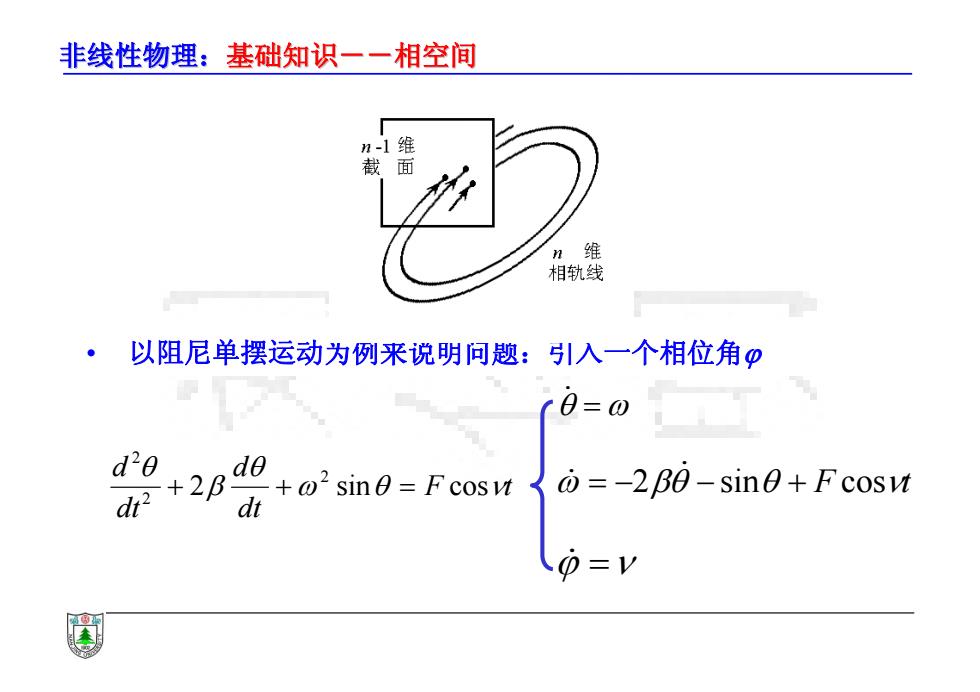
非线性物理:基础知识一一相空间 n-1维 截面 n维 相轨线 以阻尼单摆运动为例来说明问题:引入一个相位角φ 0=0 d20 d2+2B θ +2 sin0=Fcosu=-280-sin0+Fcosv dt
非线性物理:基础知识--相空间 基础知识--相空间 • 以阻尼单摆运动为例来说明问题:引入一个相位角 F t dt d dt d 2 sin cos 2 22 2 sin F cost
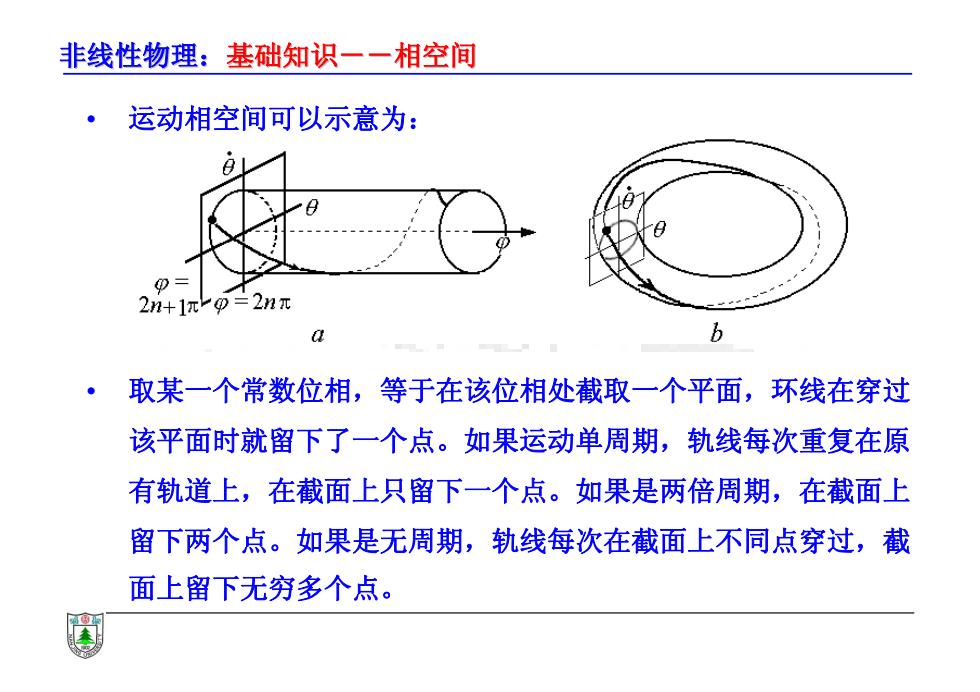
非线性物理:基础知识一一相空间 ,运动相空间可以示意为: 2n+1πp=2nπ a b ·取某一个常数位相,等于在该位相处截取一个平面,环线在穿过 该平面时就留下了一个点。如果运动单周期,轨线每次重复在原 有轨道上,在截面上只留下一个点。如果是两倍周期,在截面上 留下两个点。如果是无周期,轨线每次在截面上不同点穿过,截 面上留下无穷多个点
非线性物理:基础知识--相空间 基础知识--相空间 • 运动相空间可以示意为: • 取某一个常数位相,等于在该位相处截取一个平面,环线在穿过 该平面时就留下了一个点。如果运动单周期,轨线每次重复在原 有轨道上,在截面上只留下一个点。如果是两倍周期,在截面上 留下两个点。如果是无周期,轨线每次在截面上不同点穿过,截 面上留下无穷多个点
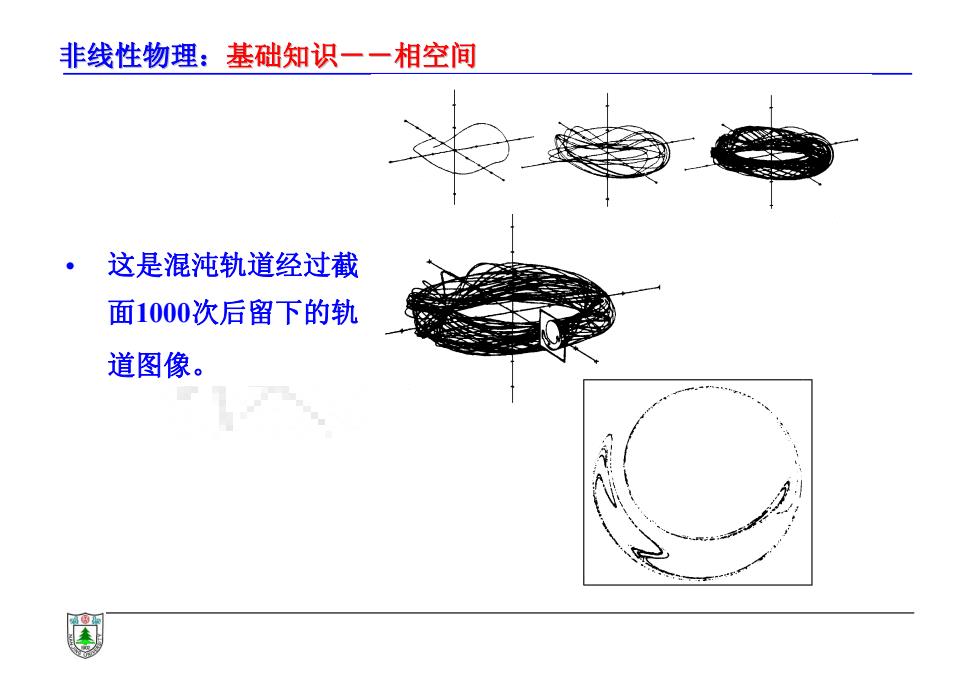
非线性物理:基础知识一一相空间 这是混沌轨道经过截 面1000次后留下的轨 道图像
非线性物理:基础知识--相空间 基础知识--相空间 • 这是混沌轨道经过截 面1000次后留下的轨 道图像

非线性物理:基础知识一一相空间 以单摆为例: ·再以带阻尼和周期驱动的单摆为例来说明庞加莱映射的应用。 0=0 =-280-sin0+Fcosvt 0=V 在F很小时,预期长时间行为是小角度周期振动,所以: d20 do +0=Fcosvt θ(t)= cos(vt-o) dt V(@2-v2)2+4B22
非线性物理:基础知识--相空间 基础知识--相空间 以单摆为例: • 再以带阻尼和周期驱动的单摆为例来说明庞加莱映射的应用。 2 sin F cost • 在 F 很小时,预期长时间行为是小角度周期振动,所以: F t dt d dt d 2 cos 2 2 cos( t ) ( ) 4 ( ) 2 2 2 2 2 F t
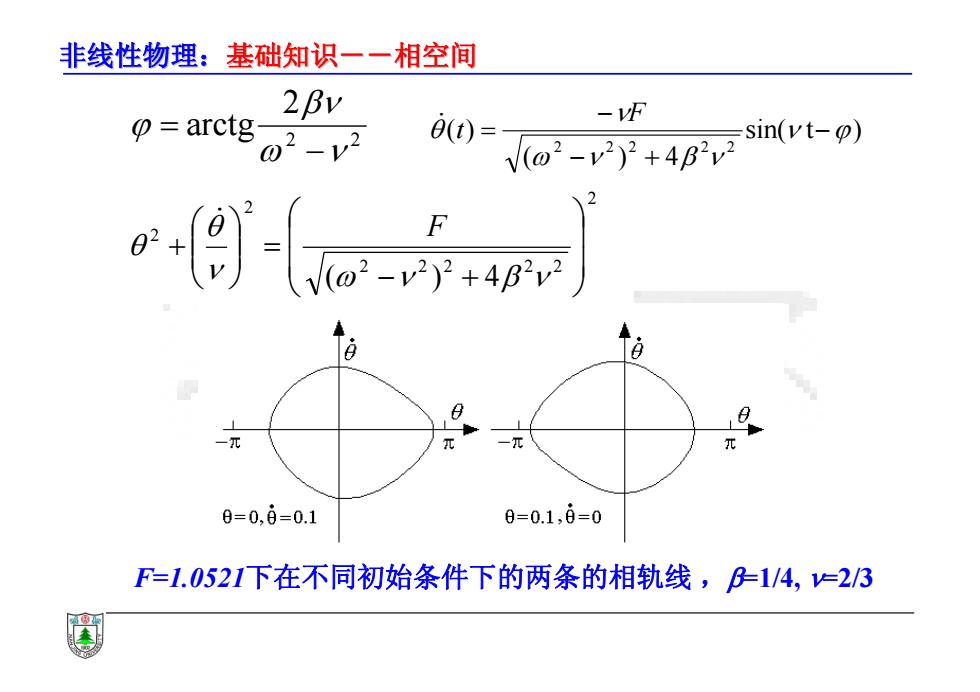
非线性物理:基础知识一一相空间 2Bv o arctg- -vF 2-v2 0(t)= V(@2-v2)2+4B2w2 sin(vt-p) B 0=0,8=0.1 0=0.1,6=0 F=1.0521下在不同初始条件下的两条的相轨线,1/4,=23
非线性物理:基础知识--相空间 基础知识--相空间 F=1.0521下在不同初始条件下的两条的相轨线 ,=1/4, =2/3 2 2 2 arctg sin( t ) ( ) 4 ( ) 2 2 2 2 2 F t 2 2 2 2 2 2 2 2 ( ) 4 F
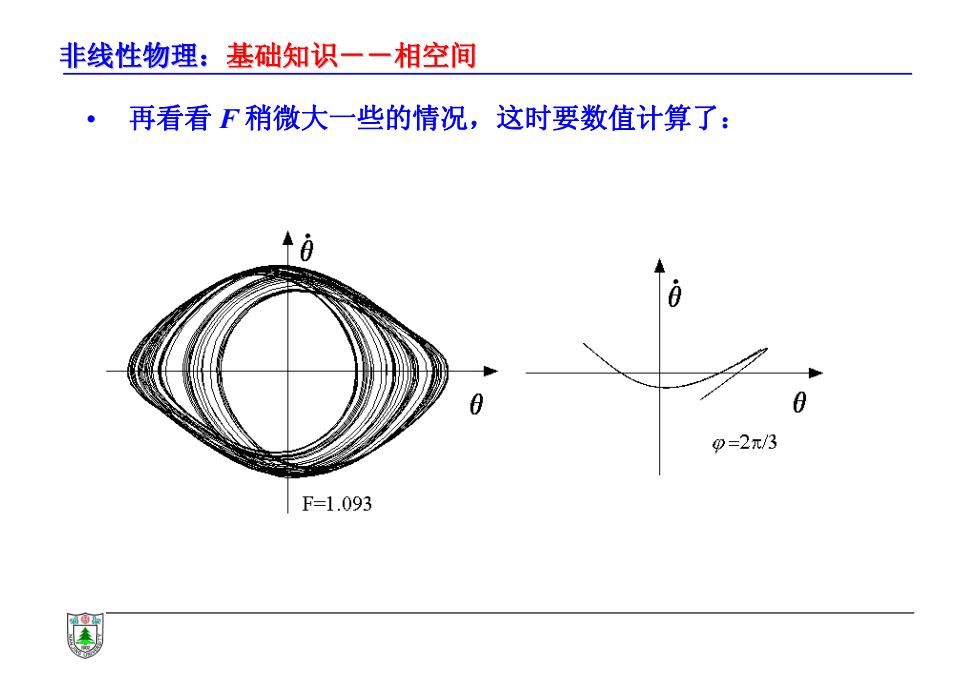
非线性物理:基础知识一一相空间 ·再看看F稍微大一些的情况,这时要数值计算了: 9=2π/3 F=1.093
非线性物理:基础知识--相空间 基础知识--相空间 • 再看看 F 稍微大一些的情况,这时要数值计算了:
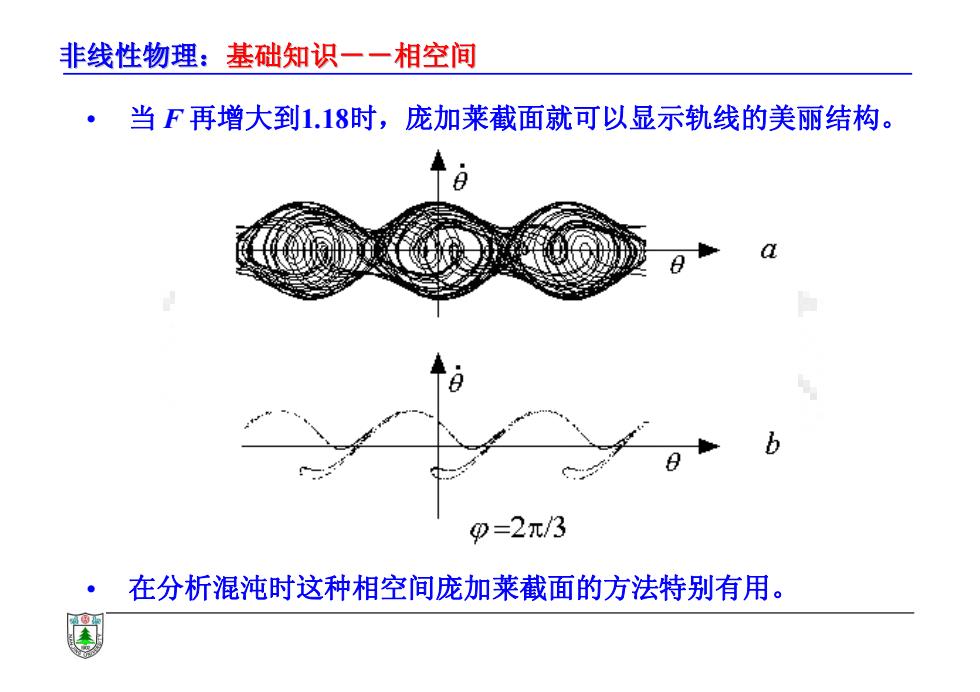
非线性物理:基础知识一一相空间 ·当F再增大到1.18时,庞加莱截面就可以显示轨线的美丽结构。 9=2π/3 在分析混沌时这种相空间庞加莱截面的方法特别有用
非线性物理:基础知识--相空间 基础知识--相空间 • 当 F 再增大到1.18时,庞加莱截面就可以显示轨线的美丽结构。 • 在分析混沌时这种相空间庞加莱截面的方法特别有用
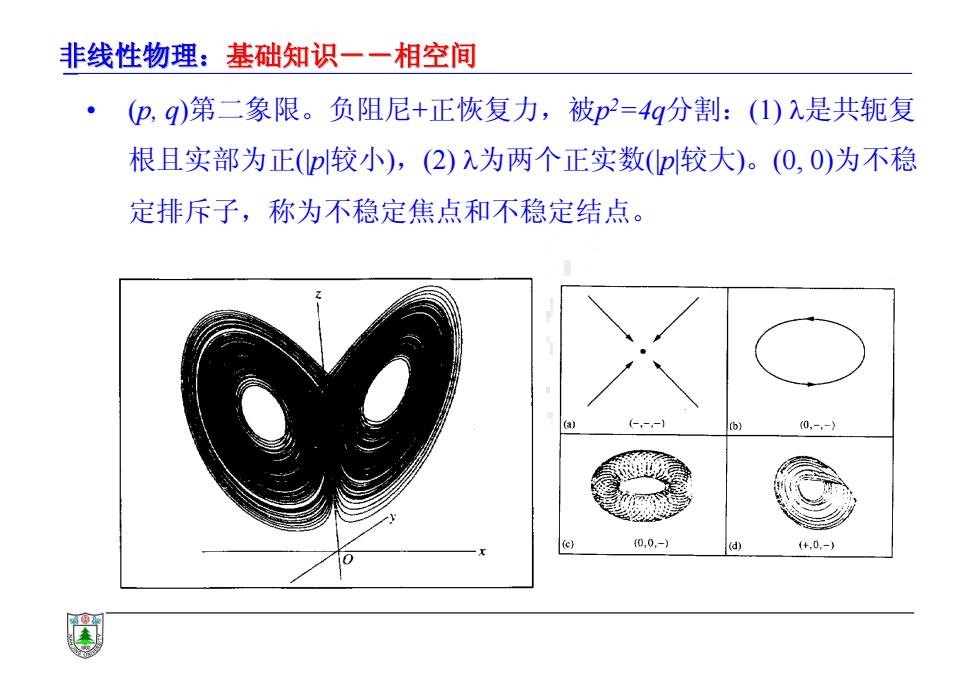
非线性物理:基础知识一一相空间 (p,q)第二象限。负阻尼+正恢复力,被p2=4g分割:(1)入是共轭复 根且实部为正(较小),(2),为两个正实数(p较大)。(0,0)为不稳 定排斥子,称为不稳定焦点和不稳定结点。 -,--1 0,-,- 0,0.-) (d) +,0,-)
非线性物理:基础知识--相空间 基础知识--相空间 • (p, q)第二象限。负阻尼+正恢复力,被p2=4q分割:(1) 是共轭复 根且实部为正(|p|较小),(2) 为两个正实数(|p|较大)。(0, 0)为不稳 定排斥子,称为不稳定焦点和不稳定结点