
第21章量子光学基出 §21.0引言 §21.1热辐射黑体辐射 §21.2普朗克的能量子假说和黑体辐射公式 §21.3光的粒子性 §21.4康普顿散射 §21.5氢原子光谱 Bohr理论 §21.6光的辐射和吸收 §21.7激光
第 21 章 量子光学基础 §21.1 热辐射 黑体辐射 §21.2 普朗克的能量子假说和黑体辐射公式 §21.3 光的粒子性 §21.4 康普顿散射 §21.5 氢原子光谱 Bohr 理论 §21.6 光的辐射和吸收 §21.7 激光 §21.0 引言
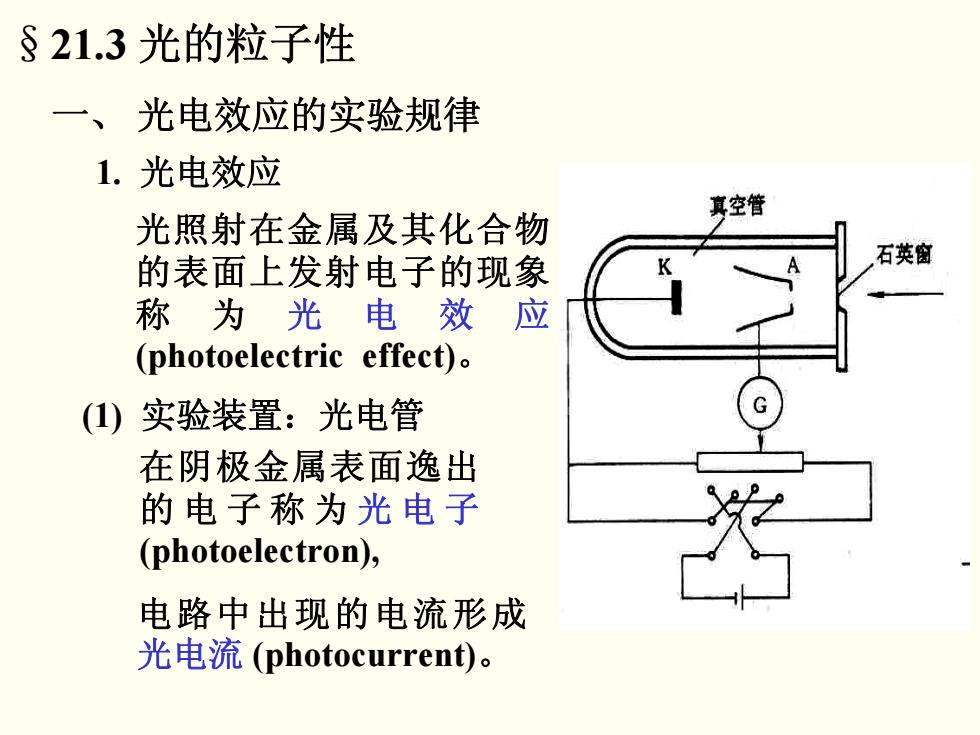
§21.3光的粒子性 一、光电效应的实验规律 1.光电效应 享空管 光照射在金属及其化合物 石英窗 的表面上发射电子的现象 称为光电效 应 (photoelectric effect). ()实验装置:光电管 在阴极金属表面逸出 的电子称为光电子 (photoelectron), 电路中出现的电流形成 光电流(photocurrent)
§21.3 光的粒子性 一、 光电效应的实验规律 1. 光电效应 光照射在金属及其化合物 的表面上发射电子的现象 称 为 光电效应 (photoelectric effect)。 (1) 实验装置:光电管 实验装置:光电管 在阴极金属表面逸出 的电子称为 光电子 (photoelectron), 电路中出现的电流形成 光电流 (photocurrent)
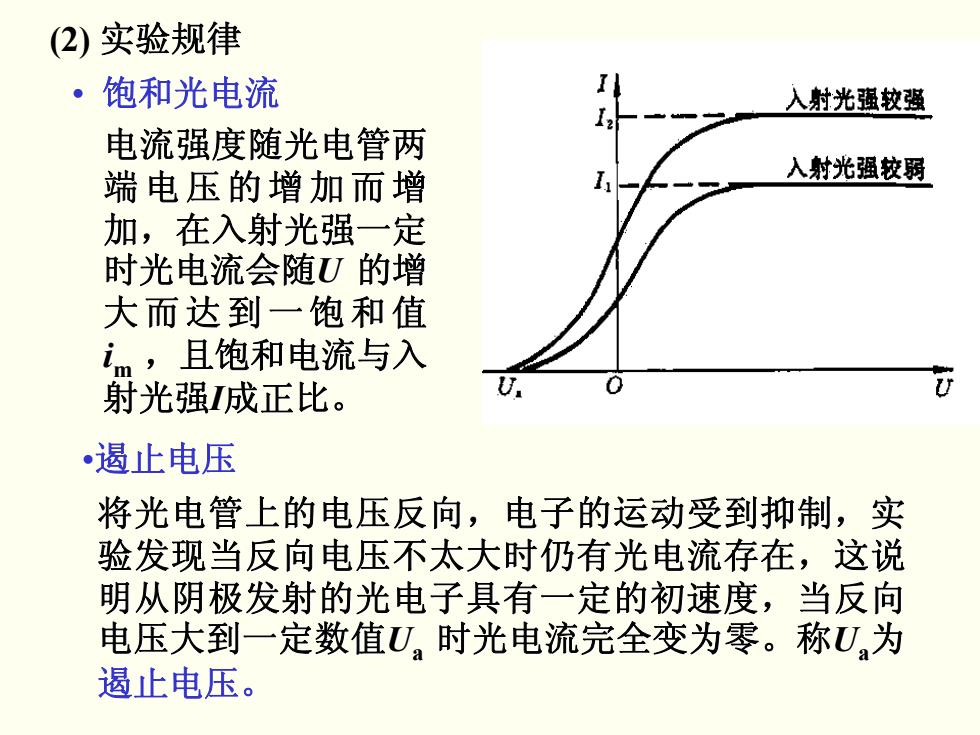
(2)实验规律 ·饱和光电流 入射光强较强 电流强度随光电管两 端电压的增加而增 入射光强校弱 加,在入射光强一定 时光电流会随U的增 大而达到一饱和值 im,且饱和电流与入 射光强成正比。 U U •遏止电压 将光电管上的电压反向,电子的运动受到抑制,实 验发现当反向电压不太大时仍有光电流存在,这说 明从阴极发射的光电子具有一定的初速度,当反向 电压大到一定数值U,时光电流完全变为零。称U为 遏止电压
• 饱和光电流 (2) 实验规律 电流强度随光电管两 电流强度随光电管两 端电压的增加而增 端电压的增加而增 加,在入射光强一定 加,在入射光强一定 时光电流会随U 的增 大而达到一饱和值 大而达到一饱和值 im ,且饱和电流与入 且饱和电流与入 射光强I成正比。 •遏止电压 将光电管上的电压反向,电子的运 将光电管上的电压反向,电子的运动受到抑制,实 动受到抑制,实 验发现当反向电压不太大时仍有光 验发现当反向电压不太大时仍有光电流存在,这说 电流存在,这说 明从阴极发射的光电子具有一定的 明从阴极发射的光电子具有一定的初速度,当反向 初速度,当反向 电压大到一定数值 电压大到一定数值Ua 时光电流完全变为零。称 光电流完全变为零。称Ua为 遏止电压
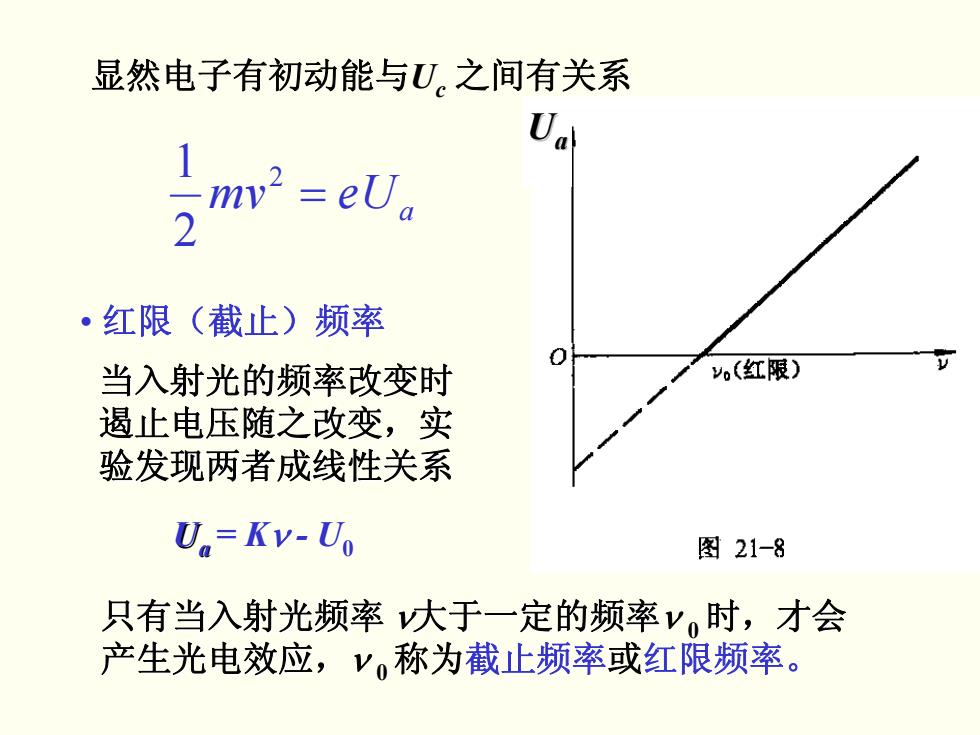
显然电子有初动能与U。之间有关系 m2=eU。 2 ·红限(截止)频率 当入射光的频率改变时 o(红限) 遏止电压随之改变,实 验发现两者成线性关系 U=Kv-Uo 图21-8 只有当入射光频率大于一定的频率y。时,才会 产生光电效应,y称为截止频率或红限频率
显然电子有初动能与 Uc 之间有关系 a = eUmv2 2 1 • 红限(截止)频率 当入射光的频率改变时 当入射光的频率改变时 遏止电压随之改变,实 遏止电压随之改变,实 验发现两者成线性关系 验发现两者成线性关系 只有当入射光频率 只有当入射光频率 ν大于一定的频率 大于一定的频率ν 0 时,才会 产生光电效应, 产生光电效应, ν 0称为截止频率 或红限频率。 Ua = Kν - U0 Ua
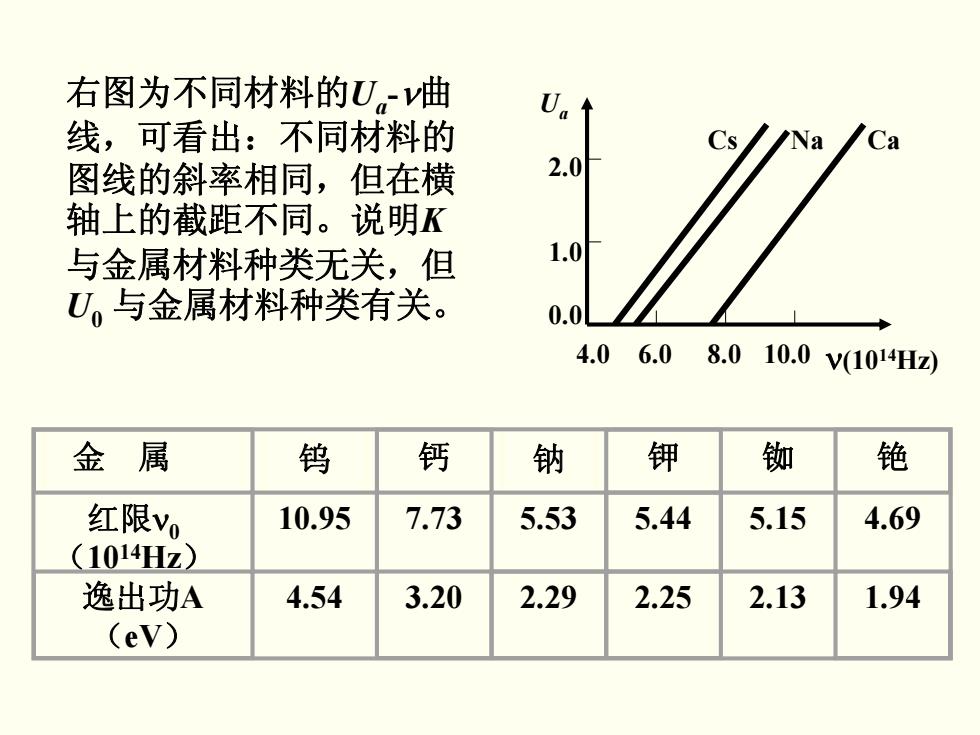
右图为不同材料的Uv曲 线,可看出:不同材料的 图线的斜率相同,但在横 2.0 轴上的截距不同。说明K 与金属材料种类无关,但 1.0 U,与金属材料种类有关。 0.0 4.06.08.010.0v(104Hz 金属 钨 钙 钠 钾 铷 铯 红限Vo 10.95 7.73 5.53 5.44 5.15 4.69 (1014Hz) 逸出功A 4.54 3.20 2.29 2.25 2.13 1.94 (ev)
4.0 6.0 8.0 10.0 ν(1014Hz) 0.0 1.0 2.0 Ua Cs Na Ca 右图为不同材料的Ua-ν曲 线,可看出:不同材料的 图线的斜率相同,但在横 轴上的截距不同。说明K 与金属材料种类无关,但 U0 与金属材料种类有关。 金 属 钨 钙 钠 钾 铷 铯 红限ν0 (1014Hz) 10.95 7.73 5.53 5.44 5.15 4.69 逸出功A (eV) 4.54 3.20 2.29 2.25 2.13 1.94

光电效应瞬时响应性质 当入射光无论如何弱,光电子在光照射的瞬间 可产生,驰豫时间不超过109s。 二、爱因斯坦的光量子假设 1.经典物理学所遇到的困难 金属表面对电子具有束缚作用,电子脱离金属表面 所需要的能量,所需的最少能量称为逸出功(wok function)。用A表示,显然有
当入射光无论如何弱,光电子在光照射的瞬间 可产生,驰豫时间不超过10-9 s 。 •光电效应瞬时响应性质 二、爱因斯坦的光量子假设 e A 1. 经典物理学所遇到的困难 经典物理学所遇到的困难 金属表面对电子具有束缚作用,电子脱离金属表面 所需要的能量,所需的最少能量称为逸出功 (work function)。用 A表示 ,显然有

E photon mv2+A=eU+A 其中Ephoton为吸收的电磁波能量。 ·按照光的经典电磁理论:光波的强度与频率无关, 电子吸收的能量也与频率无关,不存在截止频率! 若用极微弱的光照射,阴极电子积累能量达到逸出功 A需要一段时间,光电效应不可能瞬时发生!
其中Ephoton为吸收的电磁波能量。 • 若用极微弱的光照射,阴极电子积累能量达到逸出功 A需要一段时间,光电效应不可能瞬时发生! • 按照光的经典电磁理论:光波的强度与频率无关, 电子吸收的能量也与频率无关,不存在截止频率! E AeUAmv a +=+= 2 photon 21

2.爱因斯坦光量子假设(1905) 为了解释光电效应,爱因斯坦假设 ()光是由一颗一颗的光子(光量子)组成。每个光 子的能量与其频率成正比,即 E=hy (2) 一个光子只能整个地被电子吸收或放出。光量子 具有“整体性”。 (3)根据能量守恒定律,电子在离开金属面时具有的初 动能: hy= mm2+A=eUa+A 2 上式即为光电效应方程
(3) 根据能量守恒定律,电子在离开金属面时具有的初 动能: 上式即为光电效应方程 2. 爱因斯坦光量子假设 爱因斯坦光量子假设 (1905) 为了解释光电效应,爱因斯坦假设 (1) 光是由一颗一颗的光子(光量子)组成。每个光 子的能量与其频率成正比,即 E = hν a +=+= AeUAmvh 2 21 ν (2) 一个光子只能整个地被电子吸收或放出。光量子 具有“整体性

利用爱因斯坦光电方程可以解释: ·光电效应的瞬时性问题 ·电子的离开金属表面的动能至少为零,故 当v<A/h时,不发生光电效应。可发生光 电效应的最小频率即红限频率 A V。= h 不同金属的A不同,则红限频率不同
• 电子的离开金属表面的动能至少为零,故 当 ν < A/h时,不发生光电效应。可发生光 电效应的最小频率即红限频率 利用爱因斯坦光电方程可以解释: • 光电效应的瞬时性问题 不同金属的A不同,则红限频率不同。 h A ν 0 =

3.光电效应的实验验证 R.A.Millikan极力反对爱因斯坦的光子假说,花了 十年测量光电效应,得到了遏止电压和光子频率的 严格线性关系 1 mva=eU。=e(Kv-Uo) 2 〔A=eUo h=eK 由直线斜率K的测量可以确定(光电效应)普朗 克常数。 h=6.56×1034J.s
由直线斜率K的测量可以确定(光电效应)普朗 的测量可以确定(光电效应)普朗 克常数。 R.A.Millikan R.A.Millikan 极力反对爱因斯坦的光子假说,花了 极力反对爱因斯坦的光子假说,花了 十年测量光电效应,得到了遏止电压和光子频率的 十年测量光电效应,得到了遏止电压和光子频率的 严格线性关系 0 = eUA = eKh 3. 光电效应的实验验证 光电效应的实验验证 )( 21 0 2m UKeeUmv a ν −== J.s 1056.6 −34 h ×=