
第20章光的干涉和衍射 §20.1光波的相干叠加 §20.2双缝干涉 §20.3薄膜干涉 §20.4偏振光的干涉 §20.5光的衍射 §20.6光栅衍射 §20.7圆孔衍射光学仪器的分辨本领 §20.8X射线的衍射
§20.1 光波的相干叠加 §20.3 薄膜干涉 §20.4 偏振光的干涉 §20.5 光的衍射 §20.6 光栅衍射 §20.7 圆孔衍射 光学仪器的分辨本领 §20.8 X射线的衍射 第 20 章 光的干涉和衍射 §20.2 双缝干涉
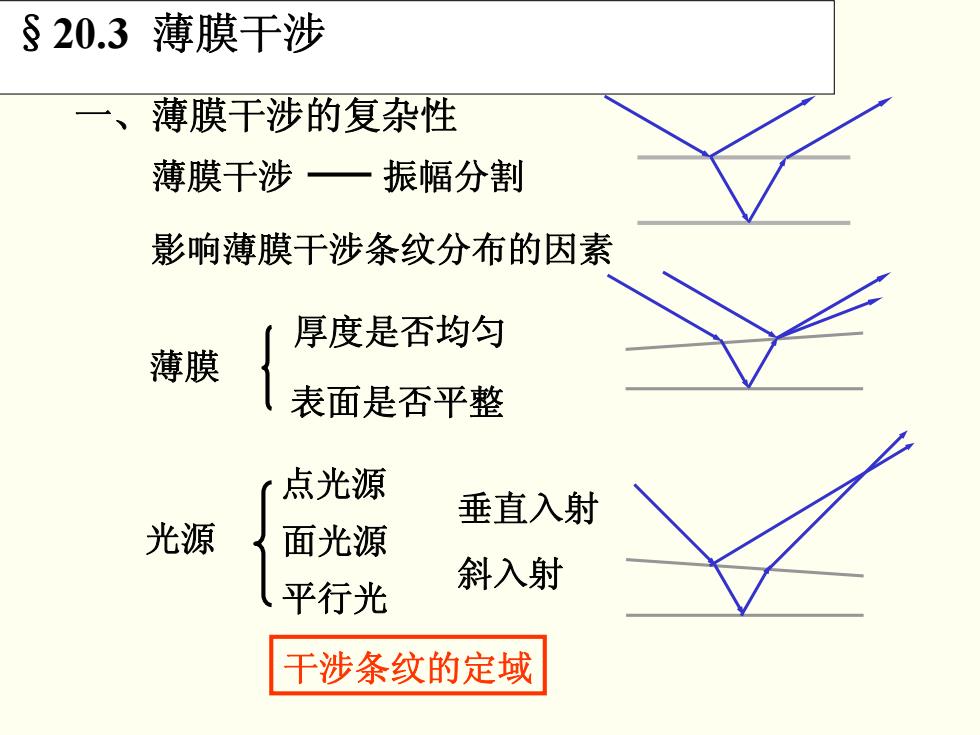
§20.3 薄膜干涉 一、薄膜干涉的复杂性 薄膜干涉一振幅分割 影响薄膜干涉条纹分布的因素 厚度是否均匀 薄膜 表面是否平整 〔点光源 垂直入射 光源 面光源 平行光 斜入射 干涉条纹的定域
一、薄膜干涉的复杂性 薄膜干涉 振幅分割 影响薄膜干涉条纹分布的因素 薄膜 光源 厚度是否均匀 表面是否平整 点光源 面光源 平行光 垂直入射 斜入射 干涉条纹的定域 §20.3 薄膜干涉

二、等倾干涉条纹 点光源照射到表面平整,厚度均 匀的薄膜上产生的干涉条纹。 δ=n,(AB+BC)-n,AD+ 2 AB=BC=d/cosr B AD=ACsini=2d.tanr.sini n1>n2 ..8=2n24-2md.tanr.sini+ d cos r n sin i=n2 sin r . d (sinrd cs 2n,d cos r 6=2dvn22-n"sin2i+ 2
d n1 n1 n 2 n1 > n 2 点光源照射到表面平整 ,厚度均 匀的薄膜上产生的干涉条纹。 二、等倾干涉条纹 r B C D 2 AD)BCAB( 2 1 λ δ n n +−+= = = cos/BCAB rd = = ⋅ ⋅sintan2sinACAD irdi 2 sintan2 cos 2 2 1 λ δ =∴ irdn +⋅⋅− r d n i A sin sin rnin1 = 2 2 cos2 2 )sin1( cos 2 2 2 2 λ λ δ r =+−=∴ rdn + r dn 2 2 sin 2 2 1 2 2 λ δ innd +−=

k入 干涉极大 当δ= 干涉极小 条纹位置由入射角确定,一定的入射 角对应同一级明条纹或暗条纹。因此 称为等倾干涉条纹。 B 条纹定域于无穷远处(透镜的焦平面上) n1>n2 对于透射光,无半波损失 8=2dvn22-n2 sin2i 与反射光所形成的条纹互补。 8=2dvn2-n'sin2i 2
d n1 n1 n2 n1 > n2 r B C i D A ( ) 当 ⎪⎩⎪⎨⎧ + = 2 12 λ λ δ k k 干涉极大 干涉极小 条纹位置由入射角确定,一定的入射 角对应同一级明条纹或暗条纹。因此 称为等倾干涉条纹。 条纹定域于无穷远处(透镜的焦平面上) 对于透射光,无半波损失 innd 2 2 1 2 2 δ = 2 − sin 与反射光所形成的条纹互补。 2 2 sin 2 2 1 22 λ δ innd +−=
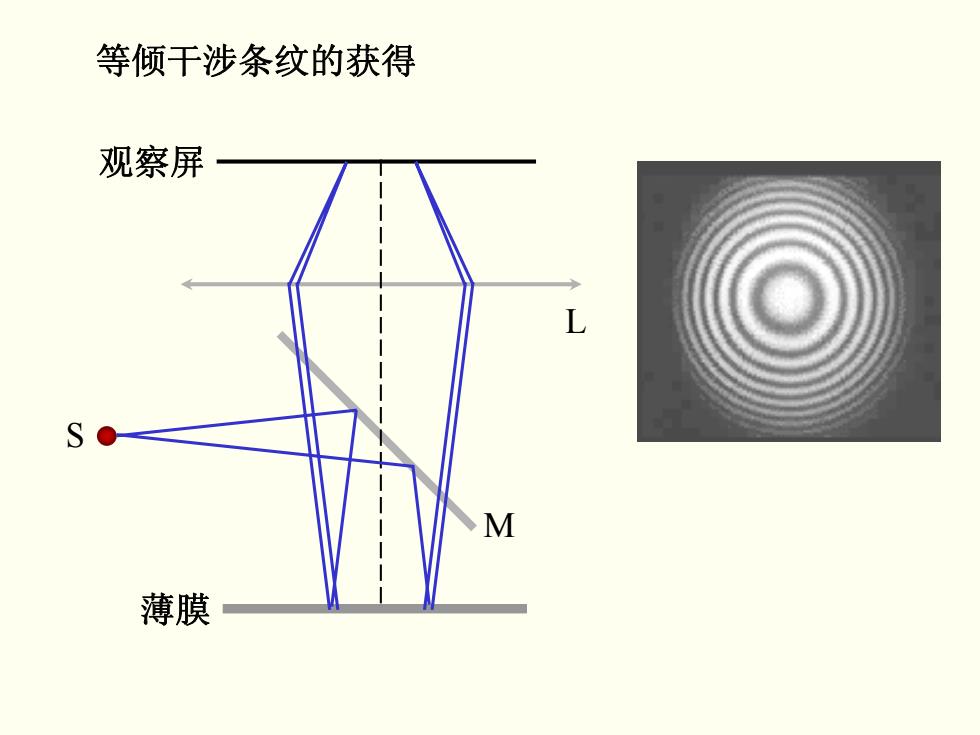
等倾干涉条纹的获得 观察屏 S 薄膜
S L M 观察屏 薄膜 等倾干涉条纹的获得

条纹特点: δ=2dVn22-n,2sin2i+ =k 2 形状:同心圆环 条纹间隔分布:内疏外密 条纹级次分布: -定时,k个→6个→i↓→?↓ 中央级次高,边缘级次低 膜厚变化时,条纹的移动:k一定时,d个→i个→个 条纹由中央冒出 波长对条纹的影响: k,d一定时,1个→i↓→r↓ 若改用面光源照明,条纹不变,明条纹亮度增加
条纹特点: 形状: 同心圆环 条纹间隔分布: 内疏外密 条纹级次分布: d一定时, k δ ri k ↓↓→↑→↑→ 膜厚变化时,条纹的移动: rid k ↑↑→↑→ 波长对条纹的影响: λ ri k ↓↓→↑→ λ λ δ −= =+ kinnd 2 2 sin 2 2 1 2 2 k一定时, k,d一定时, 中央级次高,边缘级次低 条纹由中央冒出 若改用面光源照明,条纹不变,明条纹亮度增加

「例20-41如用白光垂直入射到空气中厚为320m的肥皂 膜上(其折射率=1.33),问肥皂膜呈现什么色彩? =k 2nd 解: 2nd 2 k-1/2 取k=1,2,3代入上式,分别得: 2=4nd=1700nm 红外 4 22 =-nd=567nm 黄光! 3 4 -nd 341nm 紫外
[例20-4] 如用白光垂直入射到空气中厚为320nm的肥皂 膜上(其折射率n=1.33),问肥皂膜呈现什么色彩? 解: λ λ =+ knd 2 2 21 2 − = k nd λ λ1 = nd = nm17004 nm567 3 4 λ2 nd == nm341 5 4 λ3 nd == 黄光! 取 k = 1,2,3代入上式,分别得: 红外 紫外
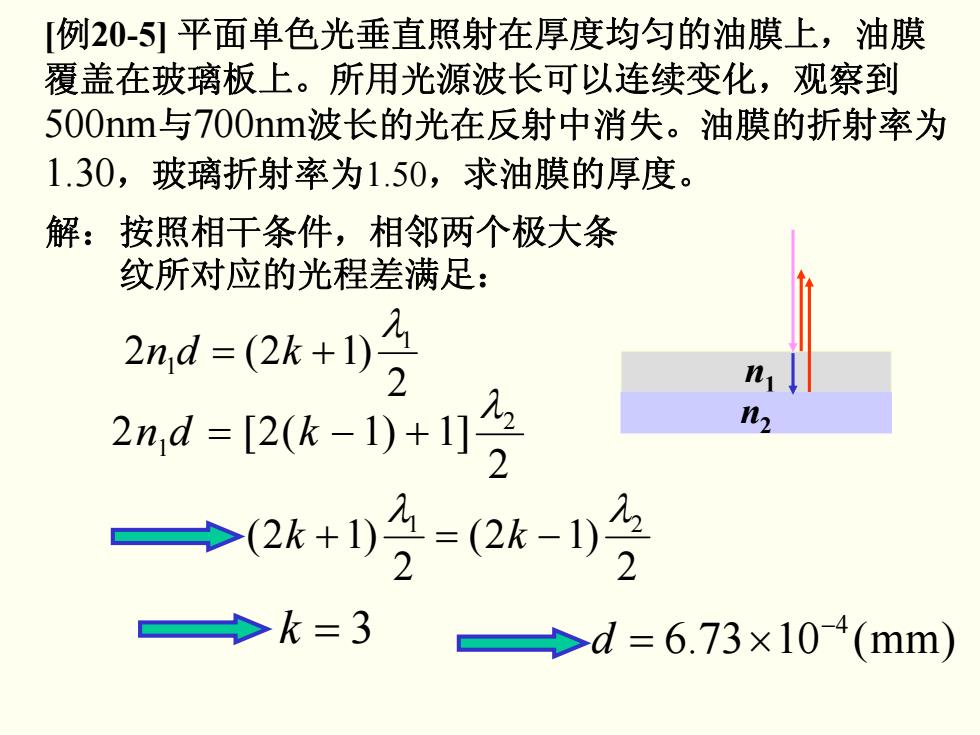
[例20-5]平面单色光垂直照射在厚度均匀的油膜上,油膜 覆盖在玻璃板上。所用光源波长可以连续变化,观察到 500nm与700nm波长的光在反射中消失。油膜的折射率为 1.30,玻璃折射率为1.50,求油膜的厚度。 解:按照相干条件,相邻两个极大条 纹所对应的光程差满足: 2md=(2k+2 2n,d=[2(k-1)+1]5 n2 →2+19-2&-1月 →k=3 >d=6.73×104(mm)
[ 例20-5] 平面单色光垂直照射在厚度均匀的油膜上,油膜 覆盖在玻璃板上。所用光源波长可以连续变化,观察到 500nm 与700nm波长的光在反射中消失。油膜的折射率为 1.30,玻璃折射率为1.50,求油膜的厚度。 解: n 1 n 2 2 )12(2 1 1 λ kdn += 2 ]1)1(2[2 2 1 λ kdn +−= 2 )12( 2 )12( λ1 λ2 k k −=+ k = 3 )mm(1073.6 − 4 d ×= 按照相干条件,相邻两个极大条 纹所对应的光程差满足:
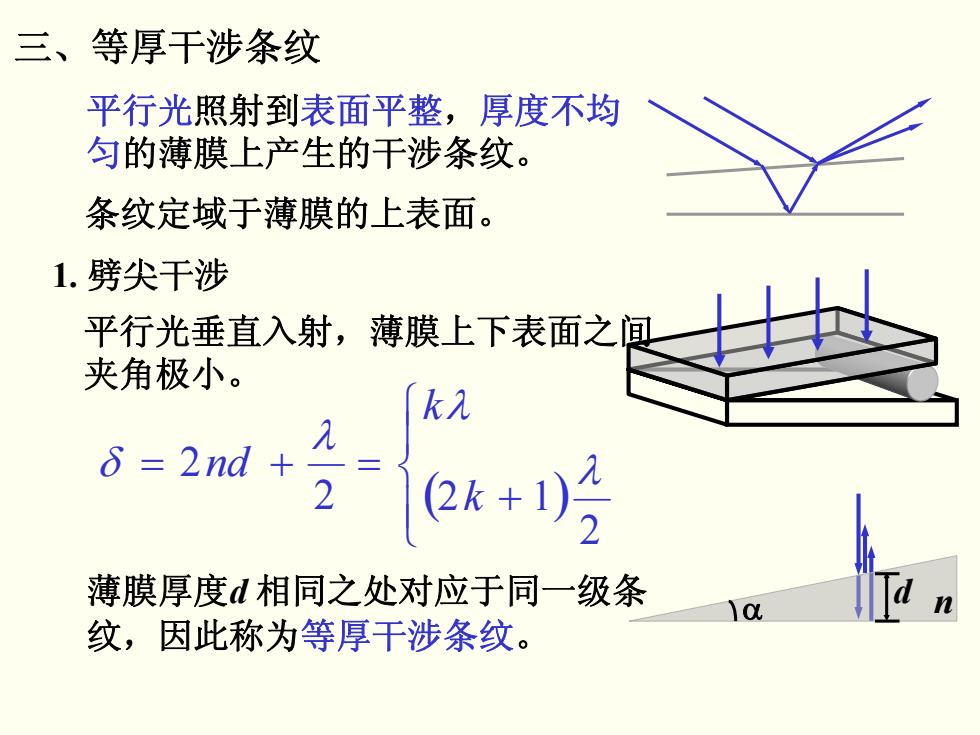
三、等厚干涉条纹 平行光照射到表面平整,厚度不均 匀的薄膜上产生的干涉条纹。 条纹定域于薄膜的上表面。 1.劈尖干涉 平行光垂直入射,薄膜上下表面之闻 夹角极小。 k δ=2nd+ Q+月 薄膜厚度d相同之处对应于同一级条 纹,因此称为等厚干涉条纹
三、等厚干涉条纹 平行光照射到表面平整,厚度不均 匀的薄膜上产生的干涉条纹。 条纹定域于薄膜的上表面。 1. 劈尖干涉 平行光垂直入射,薄膜上下表面之间 夹角极小。 α n 薄膜厚度d 相同之处对应于同一级条 d 纹,因此称为等厚干涉条纹。 ( ) ⎪⎩ ⎪⎨⎧ + = + = 2 2 2 1 2 λ λ λ δ k k nd

入 条纹特点:8=2nd+ =k入 2 形状:平行于劈尖的直条纹 条纹级次分布:厚度越大,级次越高。劈尖处为0级暗条纹。 条纹间隔分布:d,1一d。= 九 2n 相邻明(暗)条纹对应的薄膜厚度 差相等,为该媒质中的半个波长。 条纹等间距分布。 相邻条纹间距: 1=dis-dk sin a 2na
条纹特点: 形状:平行于劈尖的直条纹 条纹间隔分布: 条纹级次分布:厚度越大,级次越高。 λ λ δ =+= knd 2 2 α n d 劈尖处为0级暗条纹。 n d d k k 2 1 λ + − = 相邻明(暗)条纹对应的薄膜厚度 差相等,为该媒质中的半个波长。 ∴条纹等间距分布。 相邻条纹间距: α λ α n d d l k k sin 2 1 ≈ − = +