
第17章机械波 §17.1机械波的类型 §17.2机械波的速度 §17.3惠更斯原理 §17.4平面简谐波 §17.5平面波的波动方程 §17.6波的能流密度和强度 §17.7半波反射和全波反射 §17.8波的叠加和干涉现象 §17.9多普勒效应
第 17 章 机械波 §17.1 机械波的类型 §17.2 机械波的速度 §17.3 惠更斯原理 §17.4 平面简谐波 §17.5 平面波的波动方程 §17.6 波的能流密度和强度 §17.7 半波反射和全波反射 §17.8 波的叠加和干涉现象 §17.9 多普勒效应

§17.4平面简谐波 一、平面行波 设平面波沿x轴正向传播,质元沿y轴振动 设坐标原点的质元振动 y。=f(t) 则t时刻x处质元振动 y=f(-*) 此式为沿x轴正向传播平面波波动方程。 则沿x轴负向传播平面波波动方程为: y=f(t+ 2
一、平面行波 设平面波沿 x 轴正向传播,质元沿 y 轴振动 设坐标原点的质元振动 tfy )( o = 则 t 时刻 x 处质元振动 y ft x u = − ( ) 此式为沿 x 轴正向传播平面波波动方程。 则沿 x 轴负向传播平面波波动方程为: y ft x u = + ( ) §17.4 平面简谐波

二、平面简谐波 简谐波:波源作简谐振动,在波传到的区域,媒质中的 质元均作简谐振动。 设y。=Ac0s(ot+p) 波速d 假设:媒质无吸收(质元振幅均为) 任一点P 图中p点比o点落后时间: X u p:t台0:t- L 则 + 波动式
二、平面简谐波 设 = ωtAy +ϕ)cos( o 则 yA t x u = ⎛ ⎝⎜ ⎞⎠⎟ + ⎡⎣⎢ ⎤⎦⎥ cos ω ϕ m 简谐波:波源作简谐振动,在波传到的区域,媒质中的 质元均作简谐振动 。 假设:媒质无吸收(质元振幅均为A) y x o x 波速 uv 任一点p 图中p点比o点落后时间: u x : : totp −⇔ u x ——波动式

三、描述简谐波的物理量 1.相速度 等相位面沿波线向前推进的速度,即波速(单位时间波 所传过的距离)。 2.波长角波数 波长:两相邻同相点间的距离 周期T:波前进一个波长的距离所需的时间。 2元 角波数: k= 即单位长度上波的相位变化。 元 频率、波长和波速三者关系: V= 或九=uT
三、描述简谐波的物理量 1. 相速度 等相位面沿波线向前推进的速度,即波速 (单位时间波 所传过的距离 ) 。 2. 波长 角波数 波长:两相邻同相点间的距离 λ 角波数: λ 2 π k = 即单位长度上波的相位变化。 周期 T :波前进一个波长的距离所需的时间。 频率、波长和波速三者关系: λ = uT λ ν u = 或
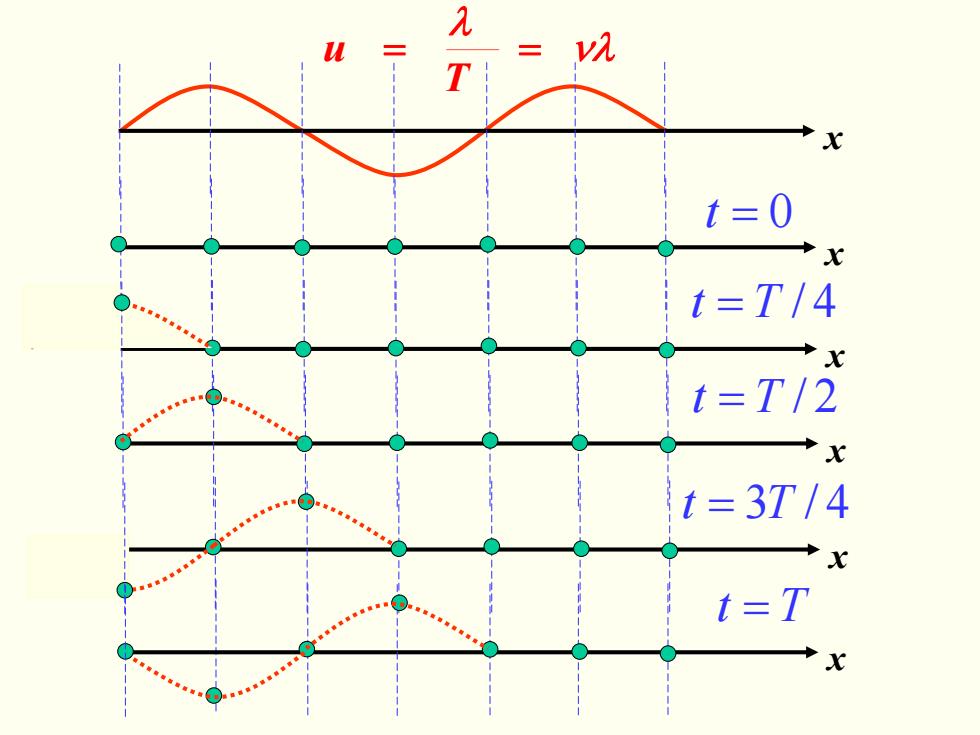
v t=0 t=T/4 X t=T/2 t=3T/4 t=T
νλ λ == T u x x t = 0 x = Tt 4/ x = Tt 2/ x = Tt 4/3 = Tt x

波动式的其它形式: y=Ac0S2πvt年S)+0 (0=2元Y) =4cos2m克+w- ,λ=uT) T =Acos[k(ut干x)+p] (k= 2元 ,u= =Acos[ot干kxr+p] 2元 2 (ku= 元 T y=Acos[@(t干)+p] 2/
波动式的其它形式: ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ = 2cos π )( +ϕν u x tAy m ω = 2( π ν ) ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ = + ϕ λ 2cos π )( x T t A m = [ m xutkA )(cos + ϕ ] = cos [ω m kxtA + ϕ ] ), 1 ( uT T λν == ), 2 π ( T uk λ λ == ) 2 π 2 π ( T uku == λ = +ϕω ])(cos[ u x tAy m

3.一维简谐波表达式的物理意义 由y(x,)=Acos@t-,从几方面讨论 a.固定x,(=x) y(xo,t)=Acos(@t-kxp) b.固定t,(t=) y(x,to)=Acos(@to-kx) c如看定某一相位,即令(ot-x)=常数 dx 相速度为: dt k d.表达式也反映了波是振动状态的传播 y(x+△x,t+△M)=x,t) 其中△x=u△t
3. 一维简谐波表达式的物理意义 a. 固定 x, (x= x0) b. 固定 t, (t = t0 ) cos(),( ) 0 0 = ω − kxtAtxy cos(),( ) 0 0 = ω − kxtAtxy c. 如 看定某一相位 , 即令 (ω t-kx)=常数 相速度为: u kt x = ω = d d d. 表达式也反映了波是振动状态的传播 由 = ω −kxtAtxy )cos(),( 从几方面讨论 Δ+ +Δ = txyttxxy ),(),( 其中Δ x=uΔ t

e.表达式还反映了波的时间、空间双重周期性。 T时间周期性 λ空间周期性 = T >注:相位差和波程差的关系 △x △0=±2元
e. 表达式还反映了波的时间、空间双重周期性。 T 时间周期性 λ 空间周期性 kT u λ ω == ¾注:相位差和波程差的关系 λ ϕ Δx ±=Δ 2π
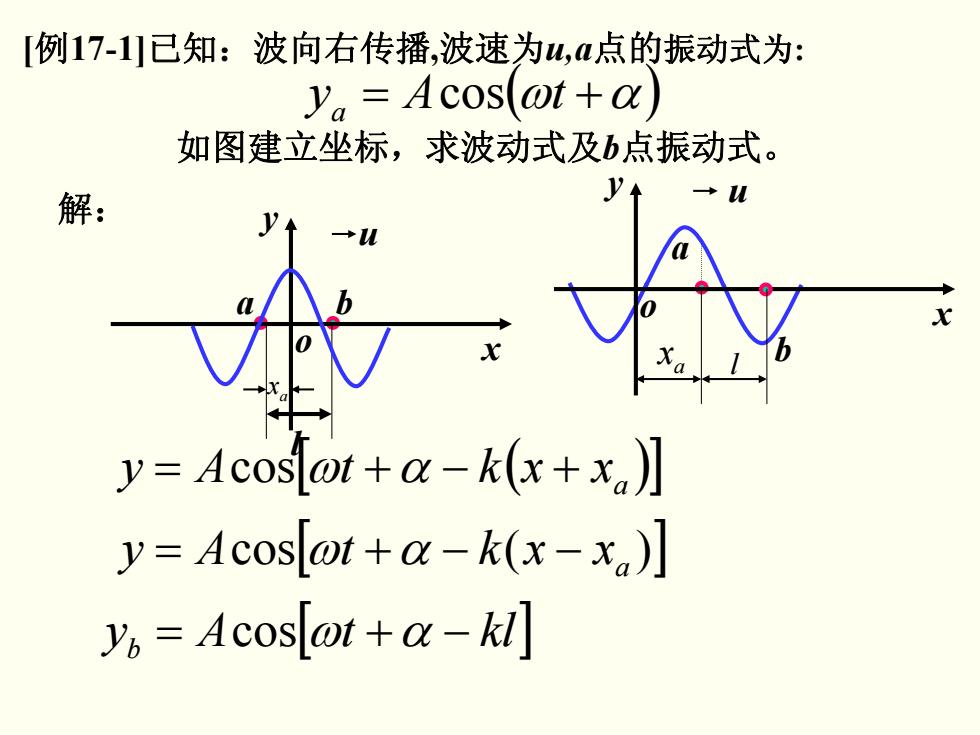
[例17-1已知:波向右传播,波速为山,点的振动式为: y。=Acos(ot+) 如图建立坐标,求波动式及b点振动式。 解: y=Acos[ot+a-k(x+x)】 y=Acos@t-+a-k(x-xa)】 y,Acos wt+a-kl]
[例17-1]已知:波向右传播,波速为u,a点的振动式为: = (ωtAy +α) a cos 如图建立坐标,求波动式及b点振动式。 cos[ )( ] a = ω +α − − xxktAy [ kltAy ] b = cos ω +α − [ ( )] a = cos ω +α − + xxktAy 解: a x x y o u a b l x y o u a b a x l

[例17-2]一横波在弦上传播,波动式为: y=0.02cosπ(5x-200t) 求:(1)A,yT,u(2)如弦的单位质量为0.5kgm,求 张力。 解: y=0.02c0s5π(x-40t) 2π y=Acos (x-ut) 2π u=40m·s1 5元 元=0.4m 元 T=2=0.01sy= 元 1 =100Hz A=0.02m u T
解: y = 5cos02.0 π − tx )40( )( 2π = cos − utxAy λ 1 sm40 − u ⋅= 5π 2π = λ λ = m4.0 == s01.0 u T λ Hz100 1 == T ν A = m02.0 [例17-2]一横波在弦上传播,波动式为: 求:(1)A , ν, T , u (2)如弦的单位质量为0.5kg/m,求 张力。 y = cos02.0 π − tx )2005(