
第17章机械波 §17.1机械波的类型 §17.2机械波的速度 §17.3惠更斯原理 §17.4平面简谐波 §17.5平面波的波动方程 §17.6波的能流密度和强度 §17.7半波反射和全波反射 §17.8波的叠加和干涉现象 §17.9多普勒效应
第 17 章 机械波 §17.1 机械波的类型 §17.2 机械波的速度 §17.3 惠更斯原理 §17.4 平面简谐波 §17.5 平面波的波动方程 §17.6 波的能流密度和强度 §17.7 半波反射和全波反射 §17.8 波的叠加和干涉现象 §17.9 多普勒效应
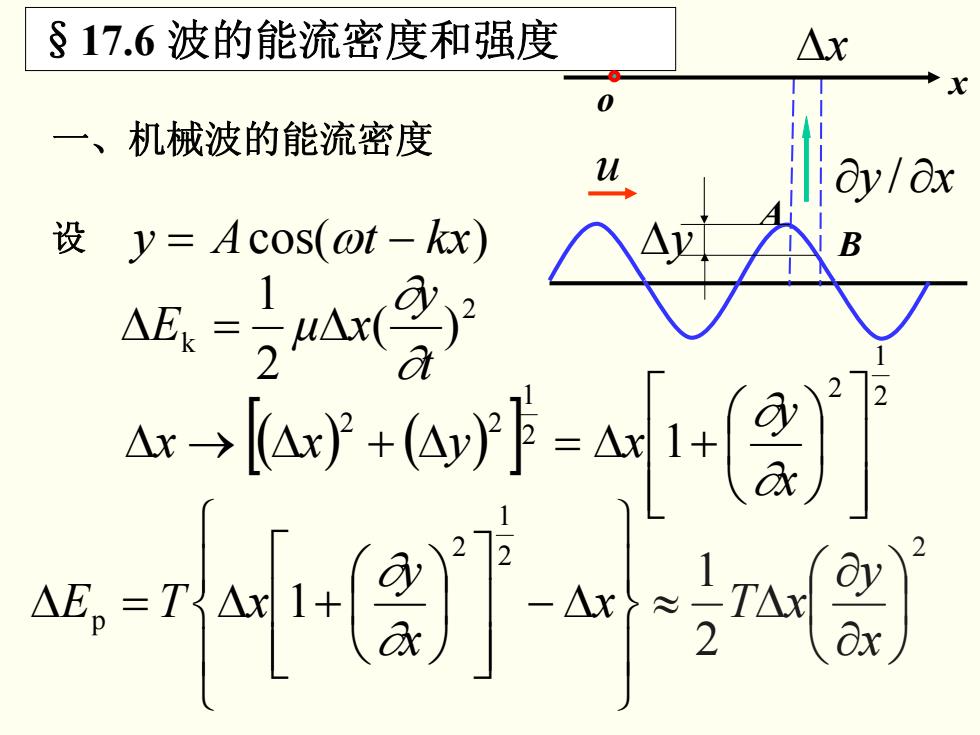
§17.6波的能流密度和强度 △x 一、机械波的能流密度 设y=Acos(ot-kx) A迟.方a sn-w+f-ae 小
一、机械波的能流密度 设 y A t kx = cos( ) ω − 2 k )( 2 1 t y E μ x ∂ ∂ Δ=Δ [ ] () () 2 1 2 2 1 2 2 1 ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ +Δ=Δ+Δ→Δ x y xyxx ∂ ∂ ⎪ ⎭ ⎪ ⎬ ⎫ ⎪ ⎩ ⎪ ⎨ ⎧ Δ− ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ +Δ=Δ x x y xTE 2 1 2 p 1 ∂ ∂ 2 2 1 ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ∂ ∂ Δ≈ x y xT §17.6 波的能流密度和强度 u A B x o Δx Δy ∂ / ∂xy

对于平面简谐波 sink) AF=TAx'sin(-k) 2 T .‘u= △E=△E。(同步变化) k △E=△xuo2Asin(ot-kx)
2 2 pk 2 1 )( 2 1 ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ∂ ∂ Δ+ ∂ ∂ Δ=Δ+Δ=Δ x y xT t y EEE μ x 对于平面简谐波 E μ ( ) −ωωΔ=Δ kxtAx 222 k sin 2 1 Δ=Δ ( ) −ω kxtAxkTE 222 p sin 2 1 k EE p T k u Δ=Δ∴== μ ω Q ΔE x A t kx = Δ μω ( ) ω − 22 2 sin (同步变化 )

单位体积中的机械能 △E 8= 三po2Asin(ot-x) S△x u=pS 6--fw-Tpo
单位体积中的机械能 ε = Δ Δ E S x = ρω ( ) ω − 22 2 A t kx sin 22 0 2 1 d 1 At T T == ρωεε ∫ μ = ρS
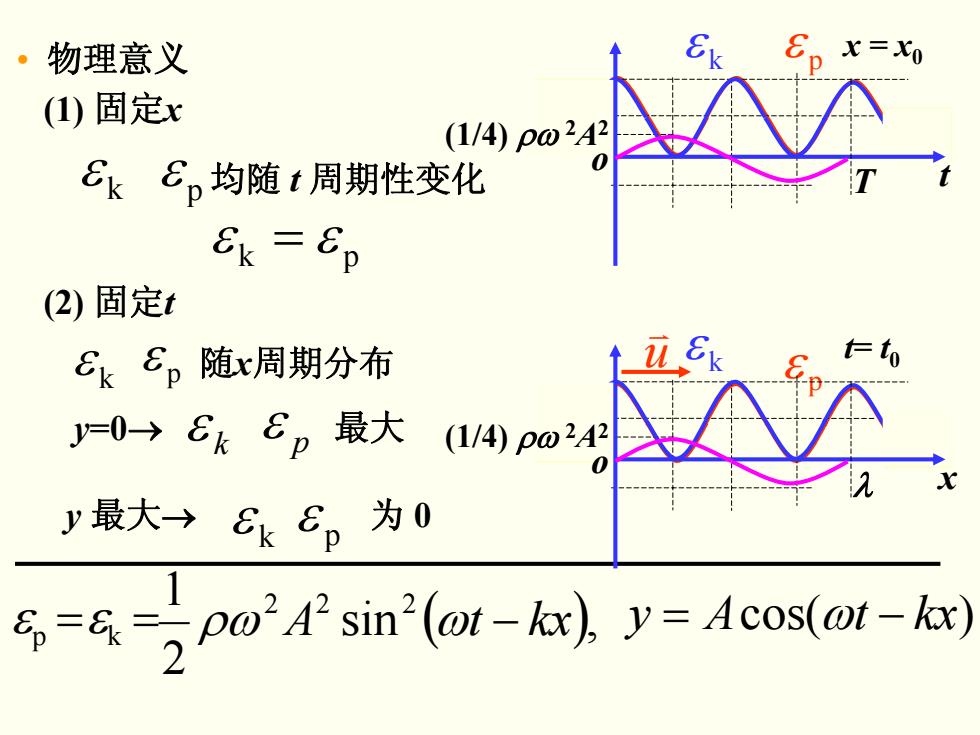
。 物理意义 。x=0 (1)固定x 11Ap02A8 CkBp均随t周期性变化 8k=8p (2)固定t EkEp随x周期分布 t=to 0→8kEp最大 (1/4)p02A2 y最大→Ek8。为0 p0 sin'(ot-ka).y=Acos(ot-k)
p ε (1) 固定x • 物理意义 (2) 固定t ε k ε p 均随 t 周期性变化 pk ε = ε ε k ε p 随x周期分布 y 最大→ 为 0 k ε p ε y=0→ ε k ε p 最大 sin ( ), 21 222 ε =ε kp = ρω ω − kxtA = ω − kxtAy )cos( p ε T ε k x = x0 t o (1/4) ρω2A2 λ t= t ε k 0 x o (1/4) ρω2A2 u v
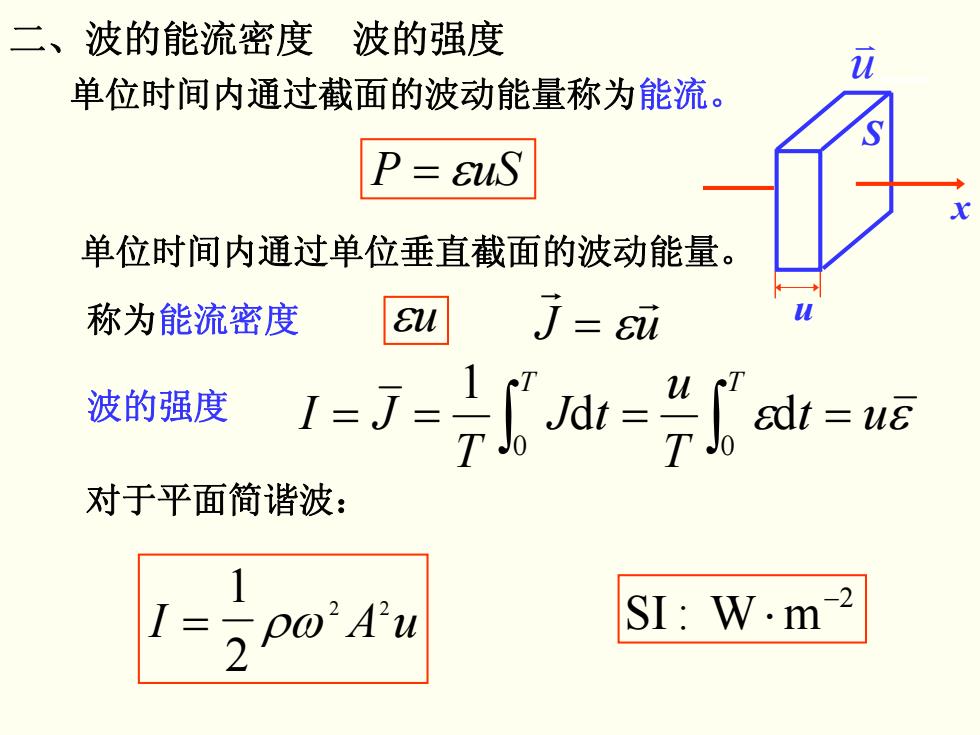
二、波的能流密度 波的强度 单位时间内通过截面的波动能量称为能流。 P=suS 单位时间内通过单位垂直截面的波动能量。 称为能流密度 j=su 波的强度 1=J=7d=ai=a运 对于平面简谐波: SI:W.m-2
r r J u = ε 波的强度 ut εε T u tJ T JI T T ==== 0 ∫∫ 0 dd 1 对于平面简谐波: I Au = 1 2 2 2 ρω 2 mW :SI − ⋅ 二、波的能流密度 波的强度 单位时间内通过截面的波动能量称为能流。 单位时间内通过单位垂直截面的波动能量。 称为能流密度 = εuSP εu S u x u v

球面简谐波的波动式: ou I2= PA o'u 在无吸收时,通过两球面的能流相等 14π2=124π3一 4=2 A V= Aoro cos(ot-kr)
球面简谐波的波动式: uAI 2 2 1 1 2 1 = ωρ uAI 2 2 2 2 2 1 = ωρ 在无吸收时,通过两球面的能流相等 1 2 2 1 r r A A = )cos( 00 krt r rA y = ω − r 2 r 1 O 2 22 2 4 π 11 = 4 πrIrI

三、声波声强级 I(W/m2)I 1.正常人听声范围 频率范围:20-20000H☑ Io=10-12W/m2 2.声强级 0201000 20000 Hz) 以1000Hz时的I下作为基准声强I 1=10-12W/m2 L=log lo 单位:Bel(贝尔) dB(分贝) ldB=Bel 10 L=101o810 √声波,超声波,次声波
三、声波 声强级 频率范围: − Hz2000020 2. 声强级 0 log II L = 12 2 0 m/W10− I = 单位: Bel(贝尔) dB (分贝) Bel 10 1 dB1 = 9声波,超声波,次声波 1. 正常人听声范围 o 20 1000 20000 I (W / m2) I上=1 I0=10-12W/m2 · ν(Hz) · 以1000 Hz 时的I下作为基准声强 I0, 0 log10 II L =

[例17-6在截面积为S的圆管中,有一列平面简谐波,其波 动的表达式为y=Ac0$(ot-2πx/几)。管中波的平 均能量密度为w,则通过截面S的平均能量是多少? 解: P=wuS 几 2元 u .T= T ① 02 u= P= ⊙入 wS 2π 2元 END
解: = uSwP T u λ Q = ω 2π Q T = 2π ωλ ∴ u = SwP 2π ωλ = END [例17-6]在截面积为S的圆管中,有一列平面简谐波,其波 动的表达式为 。管中波的平 均能量密度为w,则通过截面S的平均能量是多少? = ω − 2cos( πxtAy λ)/