
第16章变化的电兹场 §16.1电磁感应定律 §16.2动生电动势 §16.3感生电动势 感应电场 §16.4自感和互感 §16.5电容和电感电路中的暂态电流 §16.6磁场能量 §16.7位移电流 §16.8麦克斯韦电磁场方程组
第 16 章 变化的电磁场 §16.2 动生电动势 §16.1 电磁感应定律 §16.3 感生电动势 感应电场 §16.4 自感和互感 §16.6 磁场能量 §16.7 位移电流 §16.8 麦克斯韦电磁场方程组 §16.5 电容和电感电路中的暂态电流
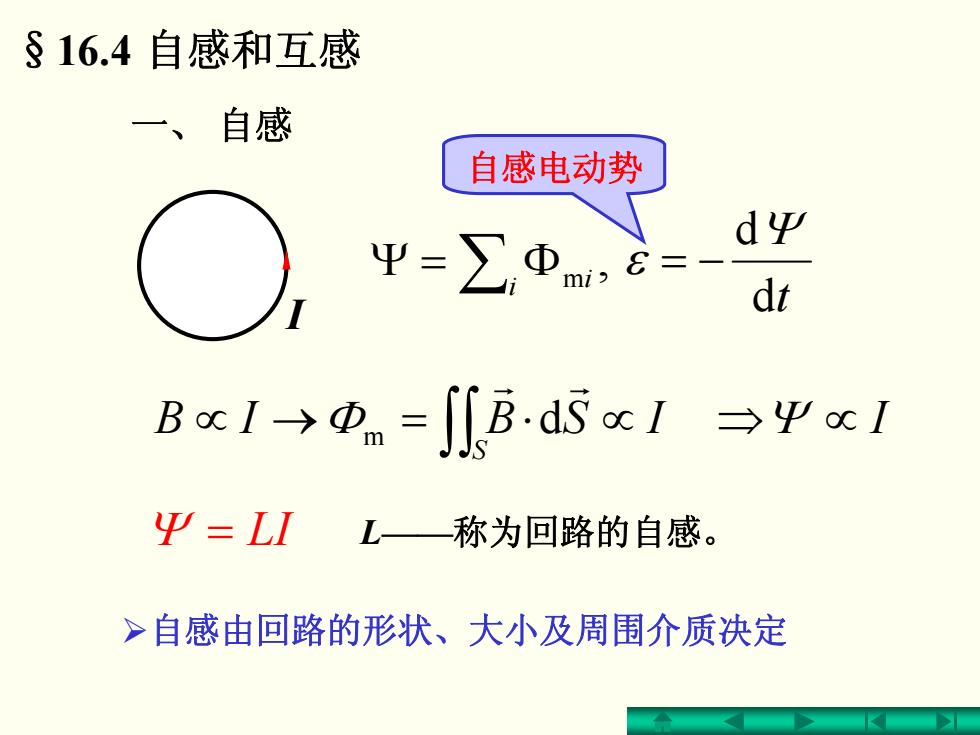
§16.4自感和互感 一、自感 自感电动势 dΨ 4=∑Φm,E= dt BcI→①n=J八B.dSc1→ΨcI Ψ=LI L—称为回路的自感。 >自感由回路的形状、大小及周围介质决定
§16.4 自感和互感 一、 自感 Ψ = LI L——称为回路的自感。 ¾自感由回路的形状、大小及周围介质决定 , ∑iΦ=Ψ mi dt dΨ ε −= IB ISB S ∝⋅=→∝ ∫∫ r r Φ m d ⇒Ψ ∝ I 自感电动势 I

dΨ dL =-L dt dr dt d 若L不变 8z=-L 自感电动势阻碍电流的变化 dt 电磁惯性 自感之单位H1H=1Wb/A 计算自感系数的方法: Ψ ●平Ψ=LI→L= d 。=-L d dt
计算自感系数的方法: I LLI Ψ Ψ =⇒=• t I L t I L L L d d d d ε ε −=⇒−=• t L I t I L t L d d d d d d −−=−= Ψ ε 若 L不变 t I L L d d ε −= = Wb/A1H1 H ——电磁惯性 自感电动势阻碍电流的变化 自感之单位

二、互感互感应 L1→平1→821 12→Ψ12→612 显然: Y21=M21 平2=M1212 可以证明:M12=M21=M回路的互感 621= dΨL=-M -1, dM dt dt dΨ2=- d2-12 M 812= dt d dt
二、 互感 互感应 21 121 Ψ = IM 12 212 Ψ = IM 可以证明: 12 = 21 = MMM t M I t I M t d d d d d d 1 21 1 21 −−=−= Ψ ε 回路的互感 t M I t I M t d d d d d d 2 12 2 12 −−=−= Ψ ε 1 → Ψ21 I 21 → ε 2 12 12 I Ψ →→ ε I1 I 2 显然:

dM 若 =0 dt =-M dl dt 62=-M d/2 dt 计算互感系数的方法: ●M Ψ2 12 。M=- 821二 812 d山 dI2 dt dt
若 0 dd = tM t I M t I M d d d d 2 12 1 ε 21 −= ε −= 计算互感系数的方法: 2 12 1 21 II M Ψ Ψ==• t I t I M d d d d 2 12 1 21 ε ε −=−=•

「例16-7]均匀长螺线管S,1外共轴地密绕两线圈, 匝数分别为N1、N2,求自感和互感。 解: B1=461 S N1 y=Ho 1 L=4o1 L2=461 N2S N1 M=Ho1 平1=N2S41 ◆M=√LL2
[例16-7] 均匀长螺线管S, l 外共轴地密绕两线圈, 匝数分别为N1、N2,求自感和互感。 1 1 01 I lN B = μ 1 21 01 SI lN Ψ = μ S l N L 21 = μ01 解: S l N L 22 = μ02 l S 1 1 0221 I lN Ψ = SN μ S lNN M 21 = μ0 = LLM 21
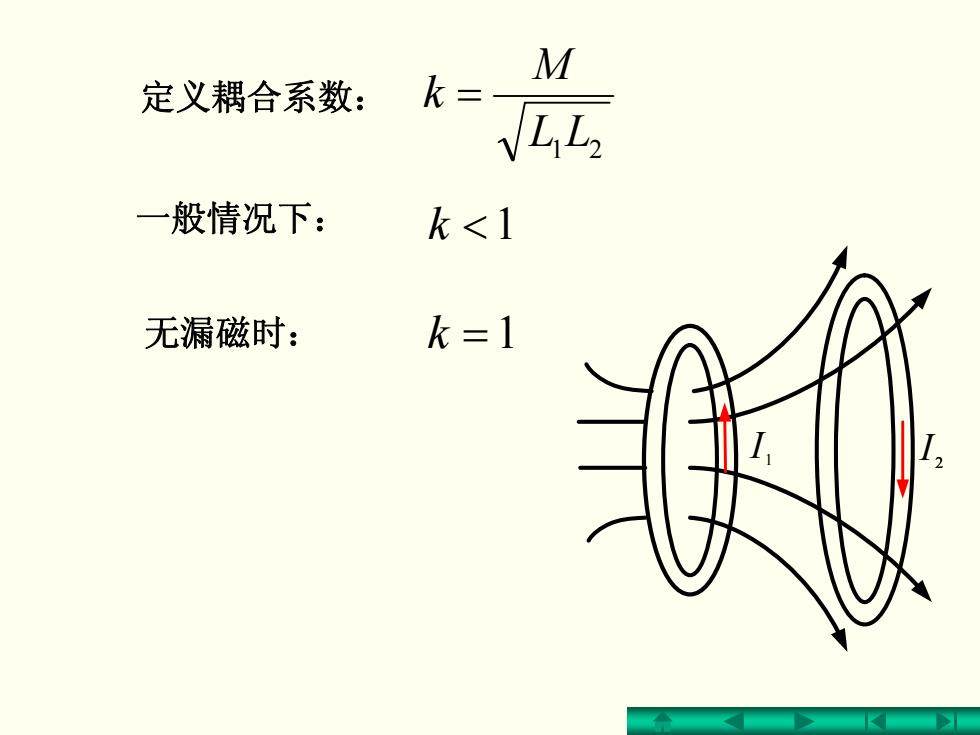
M 定义耦合系数: k= LL 一般情况下: k<1 无漏磁时: k=1
定义耦合系数: LL 21 M k = 一般情况下: k <1 无漏磁时: k =1 I1 I 2

[例16-81 如图,已知I,xo,a,b (1)回路在X处以v向右运动,求E1 回路静止于七处, d (2) >0,求82 dt (3)回路在七处以响右运动, L>0,求8 dt 解: (1)以顺时针方向为正 资性 E=Bav-B2av
I x0 a b 解: (1)以顺时针方向为正 ε = 11 − 2avBavB ⎟⎟⎠⎞ ⎜⎜⎝⎛ + = − bxx Iav 00 0 11 2π μ ,,, baxI 0 [例16-8] 如图,已知 (1)回路在 处以v向右运动,求 (2)回路静止于 处, 0 d d > t I ,求 2 ε (3)回路在 处以v向右运动, ,求 3 ε x0 x0 x0 0 d d > t I 1 ε

(2) xo +b 2元X 2元 Xo d dp(1) Moa 82= xo+b dt 2π (3) dΦ(I,xo) 83= d n5+b6a11h 2元 2元x+bx0 =81+82
0 0 0 0 ln 2 π d 2 π 0 0 x bxIa xa x bx I x + =Φ = ∫ + μ μ t I d )(d 2 Φ ε −= 0 0 0 ln 2 π d d x bx t I a + −= μ 21 = ε + ε v xbx Ia x bx t I a ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − + − + −= 0 0 0 0 0 0 11 2 π ln 2 π d d μ μ ( 2 ) t xI d ),(d 0 3 Φ ε −= ( 3 ) I x 0 a b

[例16-1两同心共面导体圆环,半径,乃(<<,) I=tk为正的常数。求变化磁场在大圆环 内激发的感生电动势。 解: M= I 12 M= 2= 1 12 12 2r2 2 →M= 2 821=- d平=-Mdl=-,x×k dt dt 2r2 END
[例16-9] 两同心共面导体圆环,半径 k为正的常数。求变化磁场在大圆环 内激发的感生电动势。 )(, 2121 << rrrr = ktI 解: 2 12 1 21 II M Ψ Ψ== , π 2 2 12 2 12 I rB I M ==Ψ 2 20 2 2r I B μ= 2 2 10 2 π r r M μ=⇒ k r r t I M t ×−=−= Ψ −= 2 2 21 10 21 2 π d d d d μ ε 1r 2r I END