专题选读14约瑟夫森效应
专题选读14 约瑟夫森效应

Brian Josephson1973年Nobel物理学奖获得者
Brian Josephson Josephson 1973年Nobel物理学奖获得者 物理学奖获得者
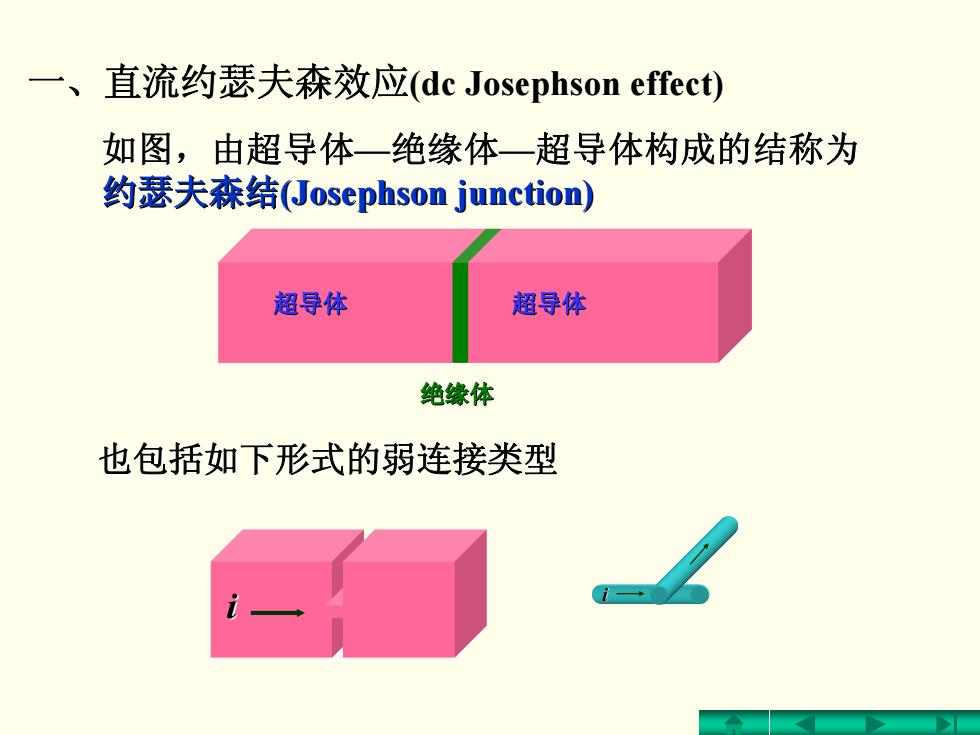
一、直流约瑟夫森效应(dc Josephson effect) 如图,由超导体一绝缘体一超导体构成的结称为 约瑟夫森结(Josephson junction) 超导体 超导体 绝缘体 也包括如下形式的弱连接类型
如图,由超导体 如图,由超导体—绝缘体—超导体构成的结称为 超导体构成的结称为 约瑟夫森结(Josephson Josephson junction) junction) 超导体 绝缘体 超导体 也包括如下形式的弱连接类型 也包括如下形式的弱连接类型 i i 一、直流约瑟夫森效应(dc Josephson effect)

问题:超导体中库珀对(通过声子场耦合在一起的 电子对)能否穿过约瑟夫森结形成隧道电流,该隧 道电流与哪些因素有关? 一自由运动的电子对应一平面波 业=Aea (1) 电子在正常导体中运动时,由于各种各样的散射, 使得电子波矢k随机变化,波函数平对空间确定的 两点x1、飞2相位差不确定。 但是,对于处于超导态的电子对(库珀对)从点x 运动到点x,由于没有散射作用存在,波函数有确定 的相位差k化2x),将其称为在宏观尺度上电子运 动相位的相干性
电子在正常导体中运动时,由于各种各样的散射, 使得电子波矢k 随机变化,波函数 Ψ 对空间确定的 两点 x 1 、 x 2相位差不确定。 ( 1 ) 一自由运动的电子对应一平面波 ikx = A e 但是,对于处于超导态的电子对(库珀对)从点 x 1 运动到点 x 2由于没有散射作用存在,波函数有确定 的相位差 k (x 2- x 1 ),将其称为在宏观尺度上电子运 动相位的相干性 。 问题:超导体中库珀对(通过声子场耦合在一起的 (通过声子场耦合在一起的 电子对)能否穿过约瑟夫森结形成隧道电流,该隧 电子对)能否穿过约瑟夫森结形成隧道电流,该隧 道电流与哪些因素有关? 道电流与哪些因素有关? ψ

现考虑两个独立的超导体S,和S,由约瑟夫森结接 触,电子在接触处的相位分别为0和0,电子的 隧穿几率应该与相位差6=(日-9)有关。根据量 子理论,Josephson给出了如下关系(理论推导 略): I=1o sin(-02)=1o sin 8 (2) 此处I为最大零电压隧穿电流(正比于电子的隧穿 几率)。 (2)式说明在零电压下,隧穿电流与相位差6=(9 日)有关,称该现象为直流约瑟夫森效应
现考虑两个独立的超导体 S 1 和 S 2 由约瑟夫森结接 触,电子在接触处的相位分别为 θ 1 和 θ 2,电子的 隧穿几率应该与相位差 δ= ( θ 1 - θ 2) 有关。根据量 子理论,Josephson 给出了如下关系(理论推导 略): = II 0 sin( θ − θ = I 021 sin) δ 此处 I0为最大零电压隧穿电流(正比于电子的隧穿 几率)。 (2)式说明在零电压下,隧穿电流与相位差 δ=( θ 1 - θ 2 )有关,称该现象为直流约瑟夫森效应 。 ( 2 )

二、 交流约瑟夫森效应(ac Josephson effect) 在约瑟夫森结上加上电压',电子对从结的一边隧 穿到另一边能量变化为E=·2qV,电子态随时间 的演化由如下因子确定 =e-2iev 利用量子理论可以证明,由于外加电场引起的相位 差6随时间的变化满足关系 88 (3) h =-2eV 8t 积分后得 =8-0,- 2eVt (4) 杭
二、交流约瑟夫森效应(ac Josephson effect ) 在约瑟夫森结上加上电压 V,电子对从结的一边隧 穿到另一边能量变化为 E= - 2qV, 电子态随时间 的演化由如下因子确定 积分后得 h 2eVt θθδ 21 −−= 利用量子理论可以证明,由于外加电场引起的相位 差 δ 随时间的变化满足关系 eV t −= 2 ∂ ∂ δ h ( 3 ) ( 4 ) iEt 2ieV ee − =

所以,隧穿电流应为 I=Io sinδ=Io sin(e,-02-2πt) (5) 其中 2eV (6) h 这样,在结上加一直流电压,会在结中产生一交变 的电流,交流电流的频率与所加直流电压成正比, 称这一有趣的现象为交流约瑟夫森效应
所以,隧穿电流应为 h 2 eV ν = 其中 这样,在结上加一直流电压,会在结中产生一交变 的电流,交流电流的频率与所加直流电压成正比, 称这一有趣的现象为交流约瑟夫森效应。 ( 5 ) ( 6 ) sin sin( 2 π ) 0 210 = δ = III θ − θ − νt

例如,1μV的直流电压对应的交流电流的频率为 483.6MHz,位于微波波段。同时高频交流超导电 流辐射同频率的电磁波。 相反,若以微波照射结,结会吸收微波导致电流的 增加。当微波的频率为时,会诱导出台阶式变化 的-V关系 1/mA V=n△U (n=1,2,.) 20 其中台阶的高度为 10 hv △U= 2e 以它作为电压测量的基准,微小电压的检查精 度可达到10-8V
例如,1μV的直流电压对应的交流电流的频率为 483.6MHz,位于微波波段。同时高频交流超导电 流辐射同频率的电磁波。 其中台阶的高度为 相反,若以微波照射结,结会吸收微波导致电流的 增加。当微波的频率为ν时,会诱导出台阶式变化 的I-V关系 = Δ nUnV = ...) ,2 ,1( e h U 2 ν =Δ 以它作为电压测量的基准,微小电压的检查精 度可达到10-8V

三、超导结的衍射效应 将约瑟夫森结放在横向磁场中,通过结的磁通量 会使两区的电子波函数产生附加的相位差,从而 改变隧穿电流,可以证明:流过约瑟夫森结的电 流由下式确定 I=1,sin(0,-02)sin(元/Φo) (7) 元Φ/Φo 对于一定材料的约瑟夫森结(日)是确定的,所以 sin(πΦ/Φo) 元Φ/Φ。 (8) 其中中是通过约瑟夫森结的磁通量中。=h/2e= 2.06785461×10-15Wb为超导磁通量子
三、超导结的衍射效应 将约瑟夫森结放在横向磁场中,通过结的磁通量 会使两区的电子波函数产生附加的相位差,从而 改变隧穿电流,可以证明:流过约瑟夫森结的电 流由下式确定 0 0 0 21 π / sin( π )/ sin( ) ΦΦ ΦΦ = II − θθ 对于一定材料的约瑟夫森结 ( θ 1 - θ 2) 是确定的,所以 0 0 m π / sin( π )/ ΦΦ ΦΦ = II 其中 Φ是通过约瑟夫森结的磁通量 Φ0= h/2e = 2.06785461 ×10-15Wb 为超导磁通量子 。 ( 7 ) ( 8 )
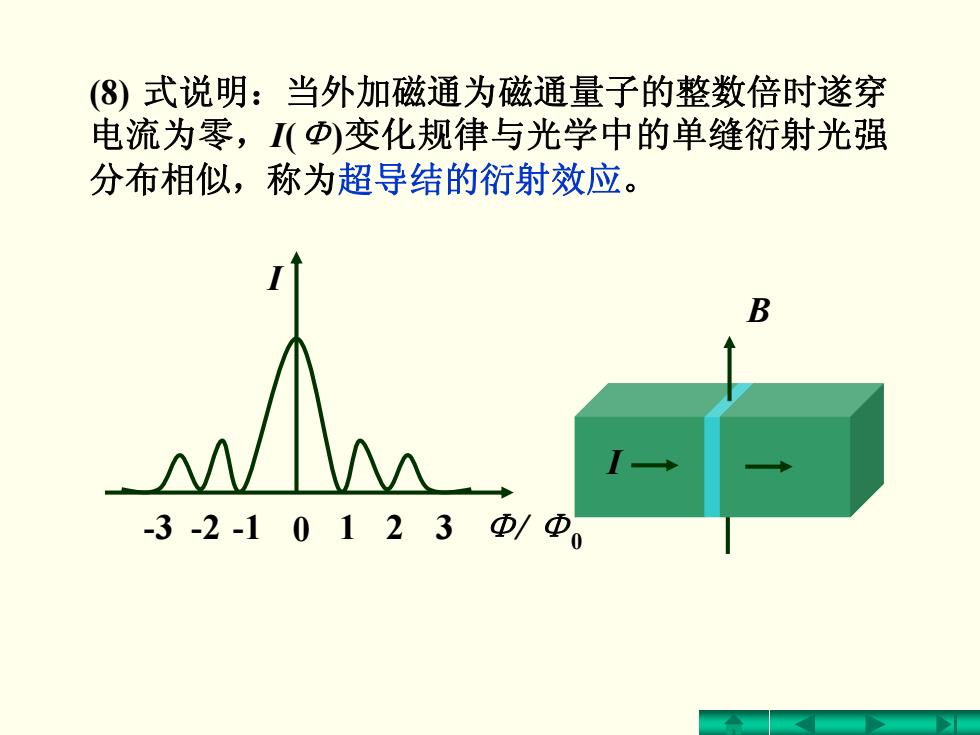
(⑧)式说明:当外加磁通为磁通量子的整数倍时遂穿 电流为零,(Φ)变化规律与光学中的单缝衍射光强 分布相似,称为超导结的衍射效应。 -3-2-10123Φ/Φ
(8) 式说明:当外加磁通为磁通量子的整数倍时遂穿 电流为零,I(Φ)变化规律与光学中的单缝衍射光强 分布相似,称为超导结的衍射效应。 0 Φ/ Φ0 -1-2-3 1 3 2 I I B