
第9章热力学定律 §9.1内能功和热量 准静态过程 §9.2热力学第一定律热容 §9.3绝热过程 多方过程 §9.4循环过程卡诺循环过程 §9.5热力学第二定律 §9.6热力学过程的不可逆性 §9.7热力学系统的熵 §9.8熵增加原理 §9.9热力学第二定律的统计意义 熵的统计表述有序和无序
§9.1 内能 功和热量 准静态过程 第 9 章 热力学定律 §9.2 热力学第一定律 热容 §9.3 绝热过程 多方过程 §9.5 热力学第二定律 §9.6 热力学过程的不可逆性 §9.7 热力学系统的熵 §9.8 熵增加原理 §9.9 热力学第二定律的统计意义 熵的统计表述 有序和无序 §9.4 循环过程 卡诺循环过程
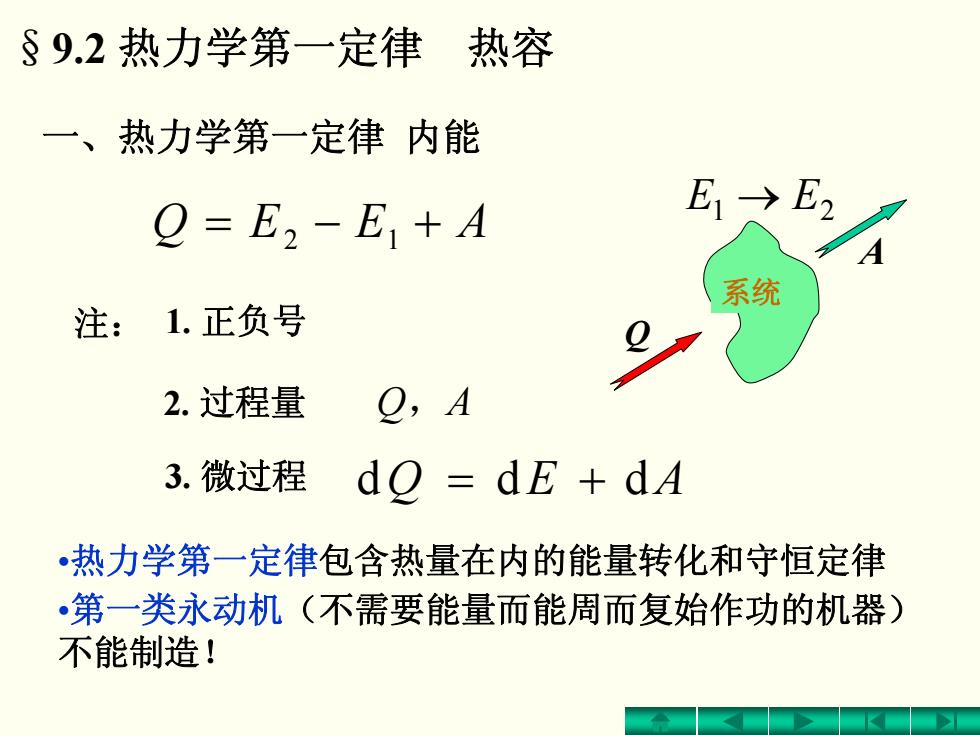
§9.2热力学第一定律热容 一、热力学第一定律内能 Q=E2-E+A E1→E2 A 系统 注:1.正负号 2.过程量 O,A 3.微过程 do =dE+dA •热力学第一定律包含热量在内的能量转化和守恒定律 •第一类永动机(不需要能量而能周而复始作功的机器) 不能制造!
Q A → EE 21 = − 12 + AEEQ 注: 1. 正负号 2. 过程量 Q,A = + ddd AEQ •热力学第一定律包含热量在内的能量转化和守恒定律 •第一类永动机(不需要能量而能周而复始作功的机器) 不能制造! 3. 微过程 一、热力学第一定律 内能 系统 §9.2 热力学第一定律 热容

二、等值过程 p 1.等容过程 dr=0 d4=0 V 对元过程 (de)=dE 对有限过程 @=R-E-2-列 =5-A
二、等值过程 1. 等容过程 = AV = 0d 0d ( )V = dd EQ ( ) )( 2 12 TTR 12 i Mm V EEQ =−= − Vpp i )( 2 −= 12 对有限过程 对元过程 0 V V p p1 p2

2.等温过程 p Pi P2 对元过程 dT=0,∴.dE=0, (do)=dA=pdy 对有限过程 Q,=(a-rg vRT In Pi=vRT In V2 1p2
2. 等温过程 T = ∴ E = ,0d ,0d () () VV RT Mm AQ VV T T 2 d 1 ∫ == 2 1 ln p p = νRT 对元过程 对有限过程 ( )T = = ddd VpAQ 1 2 ln V V = νRT 0 V1 V2 p1 p2 V p

3.等压过程 对元过程 (dO)p =dE+pdV V 对有限过程1=pdV 0 =p(V2-Y)=vR(T2-T) (O=E2-E+A =v迟(,-I)+R,-TD 2 i+2R(T-T)
( )P = + ddd VpEQ ∫ = 2 1 d VV VpA )()( = − 12 =ν −TTRVVp 12 ( )p = − 12 +AEEQ )()( 2 12 TTRTT 12 iR ν ν −+−= )( 22 TTR 12 i − + =ν 3. 等压过程 对元过程 对有限过程 0 V p p V1 V2

三、热容量 1.系统的热容:系统吸收热量与它温度变化的比值 do C= dT (1)摩尔热容量:当系统物质的量为1mo 单位:J/moK (2)比热容:当系统物质的量为1kg 单位:J/kgK dQ为过程量 C为过程量
T Q C d d = 三、热容量 (1)摩尔热容量:当系统物质的量为1mol dQ 为过程量 C 为过程量 1. 系统的热容:系统吸收热量与它温度变化的比值 (2)比热容:当系统物质的量为1kg 单位:J/mol· K 单位:J/kg· K

2.摩尔定容热容量 .m 理想气体准静态等容过程 do=dE+pdy=dEm dEm=iR 2 △E=v5RT=Cy,m△T
2.摩尔定容热容量 V V T Q C ⎟⎠⎞ ⎜⎝⎛ = d d m m, 理想气体准静态等容过程 = mm + = dddd EVpEQ m TRi E Δ=Δ 2 ν =ν V m, ΔTC V V T Q C ⎟⎠⎞ ⎜⎝⎛ = dd m m, Ri2 = TEdd m =

3.摩尔定压热容量 r-器s PV=RT p=C-→pdV=RdT +R 2
3.摩尔定压热容量 p P T Q C ⎟⎠⎞ ⎜⎝⎛ = dd m m, T p VpE ⎟⎠⎞ ⎜⎝⎛ +dm dd = →= = dd TRVpCp = RTpV RRi CP += 2 m

CP.m Cv.m +R 迈耶公式 R 热容比 Y= Cvm 2+i Y= +R R 2
P m, = V m, + RCC m, m, m, 1 V V P C R C C 热容比 γ +== i + i = 2 γ 迈耶公式 R i C V 2 RR m, = i C P += 2 m
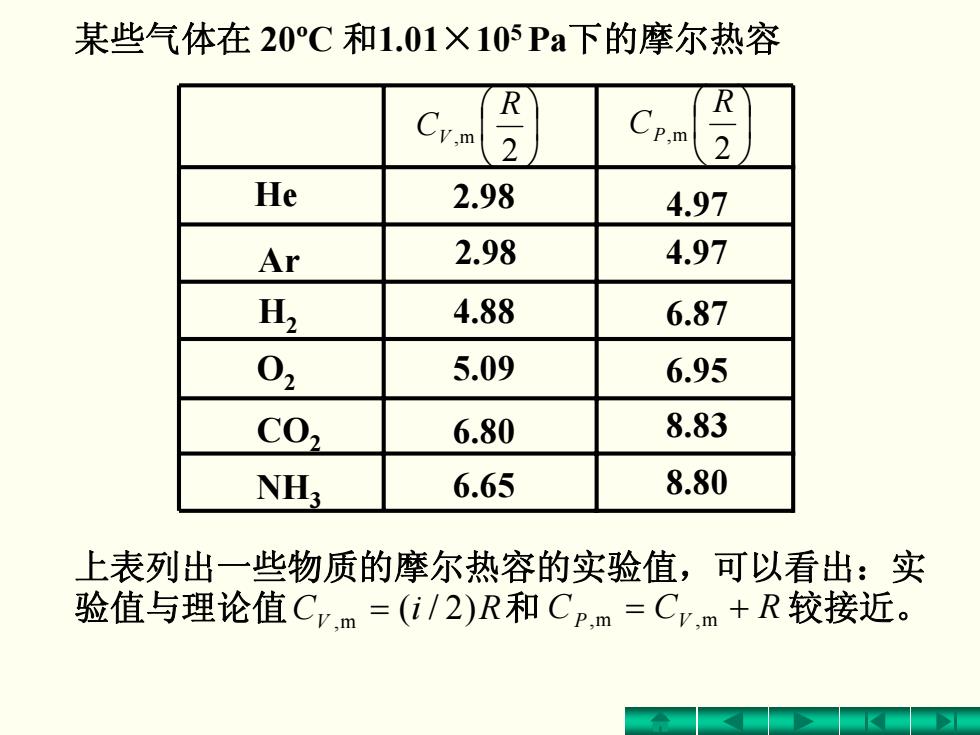
某些气体在20°C和1.01×105Pa下的摩尔热容 2 He 2.98 4.97 Ar 2.98 4.97 H 4.88 6.87 02 5.09 6.95 C02 6.80 8.83 NH; 6.65 8.80 上表列出一些物质的摩尔热容的实验值,可以看出:实 验值与理论值Cv.m=(i/2)R和Cp.m=Cv,m+R较接近
某些气体在 20ºC 和1.01×105 Pa下的摩尔热容 He Ar H2 O2 CO2 NH3 ⎟⎠⎞ ⎜⎝⎛ 2 m, R CV ⎟⎠⎞ ⎜⎝⎛ 2 m, R CP 2.98 2.98 4.88 5.09 6.80 6.65 4.97 4.97 6.87 6.95 8.83 8.80 上表列出一些物质的摩尔热容的实验值,可以看出:实 验值与理论值 V m, = )2/( RiC 和 P m, V m, += RCC 较接近