
第6章振动力学基础 §6.1简谐振动动力学 §6.2简谐振动运动学 §6.3微振动的简谐近似 §6.4平行简谐振动的合成振动频谱 §6.5垂直简谐振动的合成 §6.6阻尼振动 §6.7受迫振动共振
第 6 章 振动力学基础 §6.1 简谐振动动力学 §6.2 简谐振动运动学 §6.3 微振动的简谐近似 §6.5 垂直简谐振动的合成 §6.4 平行简谐振动的合成 振动频谱 §6.6 阻尼振动 §6.7 受迫振动 共振
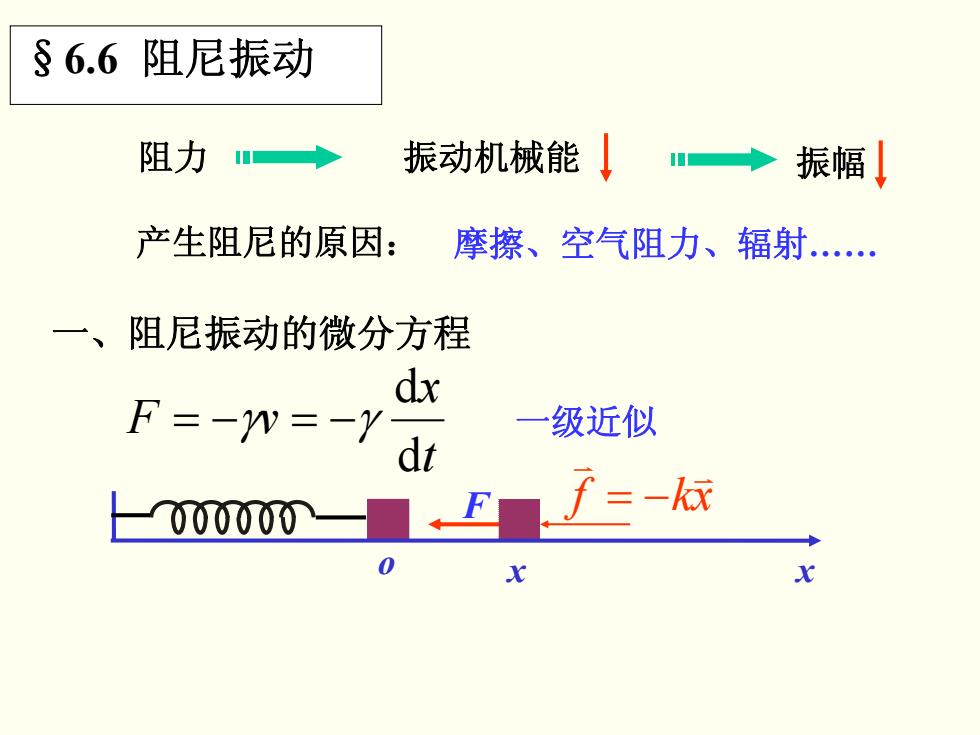
§6.6阻尼振动 阻力 振动机械能 →振幅 产生阻尼的原因: 摩擦、空气阻力、辐射.… 一、阻尼振动的微分方程 dx F=-w=-Ydi 一 级近似 000000一■.E.f=-你
阻力 振动机械能 振幅 产生阻尼的原因: 摩擦、空气阻力、辐射…… 一、阻尼振动的微分方程 t x vF d d −=−= γγ 一级近似 xkf v v −= §6.6 阻尼振动 F o x x

-kx-w=m k dt2 令:00 268= 6称为阻尼系数 m m d2x dx 动力学方程: +26 2 dt2 +0x=0 dt 物体大致的运动情况: 只有弹性力 简谐振动 加粘滞阻力后 振幅逐渐变小,即有衰减 如何衰减? 考虑以运动的物体在只有粘滞阻力作用时的运动情况
2 2 d d t x γ =−− mvkx δ 称为阻尼系数 0 d d 2 d d 2 2 0 2 x =++ t x t x 动力学方程: ωδ 物体大致的运动情况: 只有弹性力 简谐振动 加粘滞阻力后 振幅逐渐变小,即有衰减 如何衰减? 考虑以 v0 运动的物体在只有粘滞阻力作用时的运动情况。 m m k γ ω = 2, δ = 2 令: 0

dx d2x dt2 - dt 即 +2 d=0 dt2 dt dv -2 dv =-28dt dt v 积分得: lnv-ln=-2→v=y,e26 动能与时间关系: -m2-me 2 随时间指数减少
t x t x m d d d d 2 2 −= γ 即 0 d d 2 d d 2 2 =+ t x t x δ v t v 2δ d d ∴ −= t v v d2 d −= δ 积分得: t vvtvv ⋅− =⇒−=− δ δ 2 0 0 2lnln e 动能与时间关系: t mvmvE ⋅− == 42 δ 0 2 k e 21 21 随时间指数减少

可以设想:阻尼不太大时,物体一方面在弹性力作用 下振动,另一方面在粘滞力作用下振幅随时间指数地 衰减。 x=Aecos(ot+p) 方程的解:x=Ae1cos√D子δ21+0, 2元 0= 2 周期: T -82 2
( ) 0 220 cos ϕδω δ = +− − Aex t t 22 0 2π −δω T = 方程的解: 周期: ( ) 0 cos ϕω δ = + − Aex t t 22 0 −= δωω 可以设想:阻尼不太大时,物体一方面在弹性力作用 下振动,另一方面在粘滞力作用下振幅随时间指数地 衰减

讨论: >阻尼较小时(δ 阻尼较大时(δ>⊙。),质点缓慢回到平衡位置, 不作往复运动。 >当(δ=0) 时,为“临界阻尼”情况。是质点不作 往复运动的一个极限。 x=Ae cos@o2-82t+o
讨论: ( ) 0 22 0 cos ϕδω δ = +− − Aex t t ¾ 当( )时,为“临界阻尼”情况。是质点不作 往复运动的一个极限。 δ =ω0 ¾ 阻尼较小时( ),振动为减幅振动,振幅 随时间按指数规律迅速减少。阻尼越大, 减幅越迅速。振动周期大于自由振动周期。 t Ae−δ δ ω0
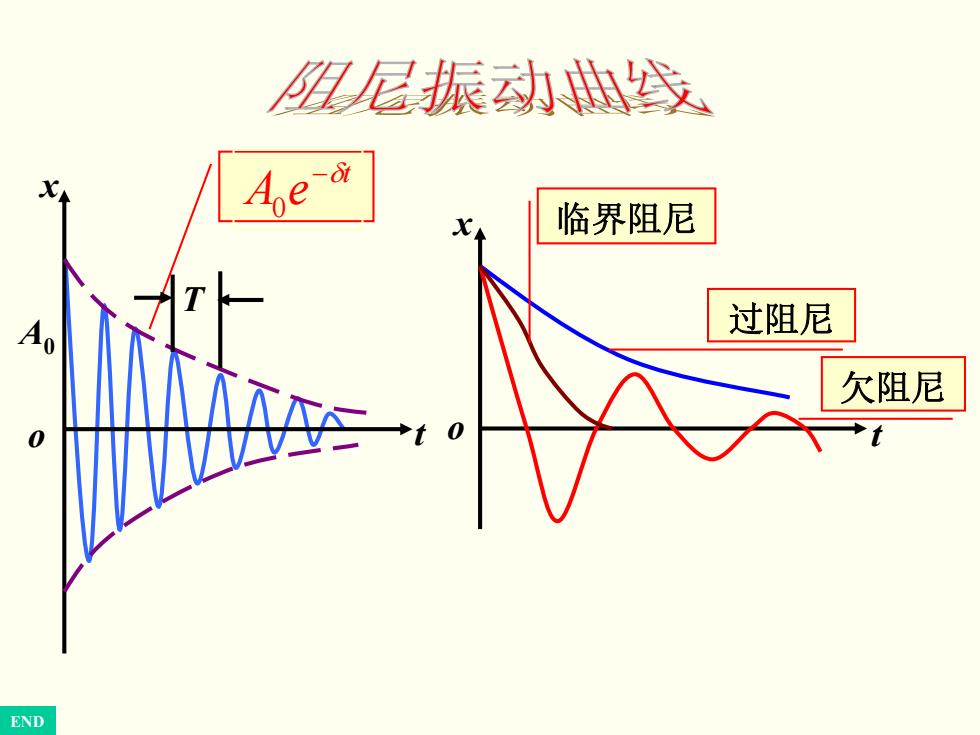
阻尼振动曲线 he-o 临界阻尼 过阻尼 欠阻尼 0 END
t x o A0 t A e−δ 0 T t x o 临界阻尼 过阻尼 欠阻尼 END