
第5章刚体力学基出 §5.1刚体运动的描述 §5.2刚体的定轴转动定理 §5.3刚体的转动惯量 §5.4刚体定轴转动的角动量守恒定律 §5.5刚体定轴转动的功能原理 §5.6回转仪进动 §5.7刚体的平面运动
第 5 章 刚体力学基础 §5.1 刚体运动的描述 §5.2 刚体的定轴转动定理 §5.3 刚体的转动惯量 §5.4 刚体定轴转动的角动量守恒定律 §5.5 刚体定轴转动的功能原理 §5.6 回转仪 进动 §5.7 刚体的平面运动

§5.6回转仪进动 讨论刚体的定点转动。 回转仪:由厚而重,形状对称的刚体绕对称 轴高速自转的装置。 当M=0时,角动量及角速度矢量保持恒定 定向回转仪。 当回转仪受到外力矩作用时,如:陀螺倾斜一? 一进动一回转效应
讨论刚体的定点转动。 回转仪:由厚而重,形状对称的刚体绕对称 轴高速自转的装置。 当 M = 0 时,角动量及角速度矢量保持恒定 ——定向回转仪 。 当 回转仪受到外力矩作用时,如:陀螺倾斜—— ? —— 进动 —— 回转效应。 §5.6 回转仪 进动

1.陀螺 设陀螺质量为m,以角速度o自转。 重力对固定点o的力矩: M=产×mg M- mgrsin 绕自身轴转动的角动量: L=J@ 由角动量定理的微分式: dI M.dt 显然,ML元,.di⊥i 乙时刻改变方向而大小不变一进动
设陀螺质量为m,以角速度ω自转。 重力对固定点o的力矩: gmrM v v v ×= = mgrM sinθ v 绕自身轴转动的角动量: ω v r c = JL 由角动量定理的微分式: ⋅= dd tML v v 显然, LM , r r ⊥ r L 时刻改变方向而大小不变——进动。 1. 陀螺 L v Ω v ω v θ mg o r v L r d dϕ LL r r d ⊥∴

d=sine.do=Josine.do d=Mdt mgrsin0.di Josine.do=mgrsine.dt 2 do mgr 进动角速度: dt J.⊙ dl 说明 1.2(或w)与w有关,与9无关。 2.进动轴通过定点且与外力平行。 3.进动方向决定于外力矩和自转角速度的方向。 4.o较小时,0有周期性变化,称为章动
θ ⋅=⋅= dsindd tmgrtMLv v LL dsind J c ⋅=⋅= dsin ϕθωϕθ v v J dsin dsin tmgr c ω θ ⋅ ϕ = θ ⋅ ω ϕ d c d J mgr t 进动角速度: Ω == 1. Ω( 或 ω p ) 与 ω 有关,与 θ无关。 Ω 2. 进动轴通过定点且与外力平行。 3. 进动方向决定于外力矩和自转角速度的方向。 4. ω 较小时, θ 有周期性变化,称为章动 。 v θ L v LLv v + d L v d dϕ o 说明
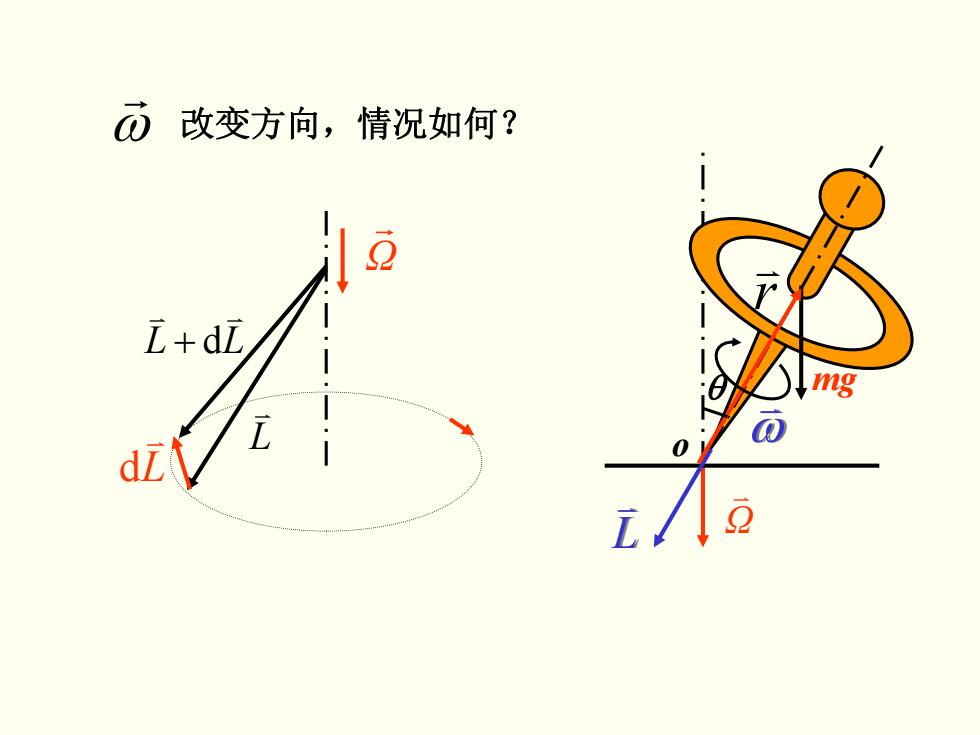
而改变方向,情况如何? i+d瓦 mg
ω r 改变方向,情况如何? Ω v L v ω v θ mg o r v L v d LL v v + d Ω r L v

2.杠杆回转仪 俯视图 0 L(t+dt) do L(t) 平衡时,保持0大小方向不变。 当重物移近时,受力矩M作用,出现回转现象。 L-J@ dl Mdt di=idp=Jdp∴.0p= do M dt J0
2. 杠杆回转仪 当重物移近时,受力矩 rM 作用,出现回转现象。 平衡时,保持 r ω 大小方向不变。 cω r r = JL ω ϕ ωϕωϕ c c p d d ddd J M t == JLL ==∴ r r r dϕ L r d tL )( r + ttL )d( r o 俯视图 r M Ω r ω r dd tML r r =

改变方向,情况如何? M。改变方向,情况如何? 俯视图 L(t) dl L(t+dt) 回转效应的应用:飞机,轮船,导弹中的指向仪, 炮筒内的旋转式来复线。 END
回转效应的应用:飞机,轮船,导弹中的指向仪, 炮筒内的旋转式来复线。 ω r 改变方向,情况如何? M p r 改变方向,情况如何? L r d d ϕ tL )( r + ttL )d( r o 俯视图 M r Ω r ω r END