
第5章利体力学基础 §5.1刚体运动的描述 §5.2刚体的定轴转动定理 §5.3刚体的转动惯量 §5.4刚体定轴转动的角动量守恒定律 §5.5刚体定轴转动的功能原理 §5.6回转仪进动 §5.7刚体的平面运动
第 5 章 刚体力学基础 §5.1 刚体运动的描述 §5.2 刚体的定轴转动定理 §5.3 刚体的转动惯量 §5.4 刚体定轴转动的角动量守恒定律 §5.5 刚体定轴转动的功能原理 §5.6 回转仪 进动 §5.7 刚体的平面运动

§5.7刚体的平面运动 刚体作平面运动时,不论运动如何复杂,总可 以分解为随质心的平动和绕通过质心轴的转动。 求解刚体平面运动的基本方程: ∑F=ma。 加上初始条件、约束条件 M。=Jad →y。,a。,0,0 动能: -m+o
刚体作平面运动时,不论运动如何复杂,总可 以分解为随质心的平动和绕通过质心轴的转动。 求解刚体平面运动的基本方程: α v r v v cc c JM i amF = =∑ 加上初始条件、约束条件 ⇒ av cc ω , , , α 动能: 2 c 2 k c 2 1 2 1 += JmvE ω §5.7 刚体的平面运动

[例5-18]长1质量m的匀质细杆放在光滑的水平面上,以 水平力垂直作用在细杆上,作用点距质心为,计算万 作用瞬间细杆的角加速度和质心的加速度。 解: F=ma M。=Fd=J.o J。 ml2 12 F 12Fd X= m ml2 d=0时,a=0,刚体只有平动没有转动
= maF c c = = JFdM cα 2 c 12 1 = mlJ c 2 12 ml Fd m F a =⇒ α = 解: d = 0 时,α = 0,刚体只有平动没有转动。 [例5-18] 长 l 质量 m 的匀质细杆放在光滑的水平面上,以 水平力 垂直作用在细杆上,作用点距质心为 d ,计算 作用瞬间细杆的角加速度和质心的加速度。 F r F r c . d F r

[例5-19]一匀质圆球(r)从静止开始沿一粗糙斜面纯滚动 而下,斜面倾角为O,球从上端滚到下端球心高度相差 为,计算小球滚到下端时质心的速度和转动角速度。 解:ng sin0-F=ma。 FN-mg cose=0 Fr=Ja mg 2 J=二mr1 5 纯滚动条件:a。=r0 V。=r0 5 10 →a.=78sin8 0= gh
[例5-19] 一匀质圆球(r )从静止开始沿一粗糙斜面纯滚动 而下,斜面倾角为θ ,球从上端滚到下端球心高度相差 为 h ,计算小球滚到下端时质心的速度和转动角速度。 c θ gm r FN r Ft 解: r ct sinθ − = maFmg 0cos N − mgF θ = = JrF ct α c = ra α sinθ 7 5 c =⇒ ga 2 c 5 2 = mrJ 纯滚动条件: c = rv ω gh r 7 101 ω =

v.=2ds=f2anising-h 0 也可由机械能守恒计算: 2 Vc -r@ → a。 5n0o 5 19 gh 10
savc = 2 c 也可由机械能守恒计算: 2 c 2 c 2 1 2 1 += Jmvmgh ω gh r 7 101 ω = ha gh 710 sin/2 = c θ = sinθ 7 5 c =⇒ ga c = rv ω
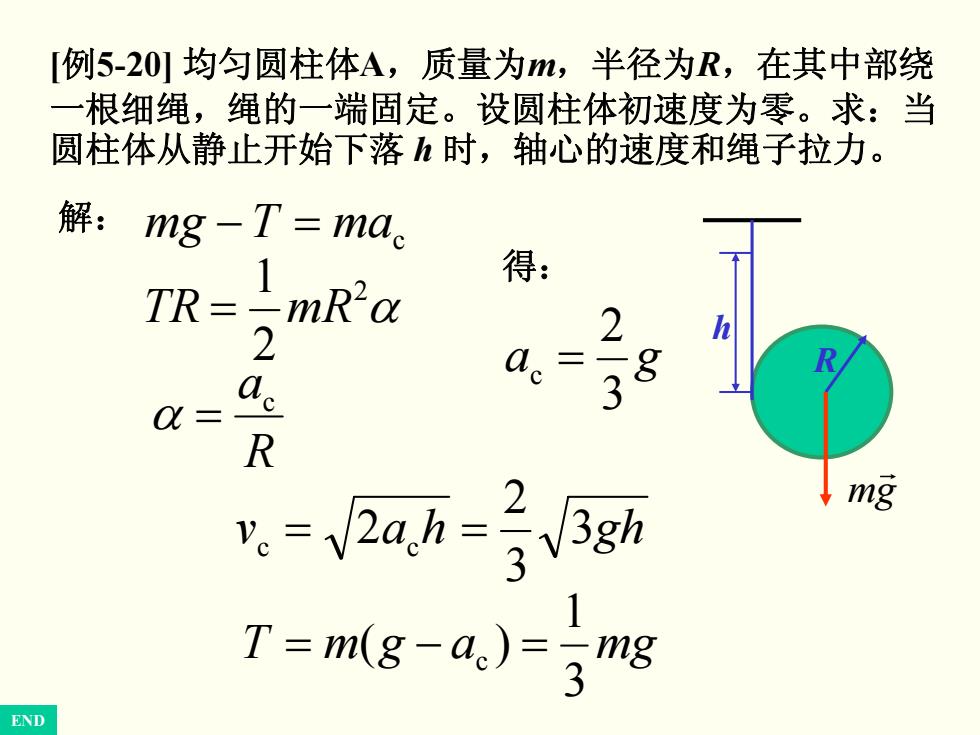
例5-20l均匀圆柱体A,质量为,半径为R,在其中部绕 一根细绳,绳的一端固定。设圆柱体初速度为零。求:当 圆柱体从静止开始下落时,轴心的速度和绳子拉力。 解: mg-T=ma 得: TR- -mR'a 2 a。 Q= R mg T-mg-a,)Smg END
[ 例5-20] 均匀圆柱体 A,质量为 m,半径为 R,在其中部绕 一根细绳,绳的一端固定。设圆柱体初速度为零。求:当 圆柱体从静止开始下落 h 时,轴心的速度和绳子拉力。 − = maTmg c 解: α 2 2 1 = mRTR R a c α = 得: ga 3 2 c = 3ghhav 3 2 2 c c == mgagmT 3 1 )( c =−= h R gm r END