
第3章机械能和功
第 3 章 机械能和功

第3章 机械能和功 §3.1功质点动能定理 §3.2保守力非保守力耗散力 §3.3质点在保守力场中的势能 §3.4质点系的势能 §3.5功能原理 能量守恒定律
第 3 章 机械能和功 §3.1 功 质点动能定理 §3.2 保守力 非保守力 耗散力 §3.3 质点在保守力场中的势能 §3.4 质点系的势能 §3.5 功能原理 能量守恒定律

§3.1功质点动能定理 一、功 功是度量能量转换的基本物理量,它描写了 力对空间的积累效应。单位为J(焦耳)。 恒力的功:A=Fcos△ =F.△F 一→ 变力的功:△A,=F,cosa,A引 b(xb36,26) A=∑cos,A =∑元A a(xaya,2a)
一、功 功是度量能量转换的基本物理量,它描写了 力对空间的积累效应。单位为J (焦耳)。 rFA r cosα Δ= F v r v Δ α 恒力的功: rF 变力的功: r r = ⋅Δ iiii rFA r cosα Δ=Δ ii i i rFA r = ∑ cosα Δ i i i rF r r ∑ Δ⋅= i αi r r Δ r Fi ),,( aaa zyxa ),,( bbb zyxb §3.1 功 质点动能定理

AdFcosads 说明子 1.一般情况下,功与力和路径有关 直角坐标系: dA=F.dr=Fdx+F,dy+F.dz A=Fd+F,d+F≠A,+A,+4 自然坐标系: A=F西=心A=rd=心Fco 2. F与参考系无关,位移与参考系有关,故 A与参考系有关
x y ++=⋅= zddddd zFyFxFrFA r r ∫ ∫ ∫ ++= b a b a b a y y z z y z x x x ddd zFyFxFA ∫∫ =⋅= b a b a rFrFA r r r dd t 自然坐标系: 2. 与参考系无关,位移与参考系有关,故 A与参考系有关。 直角坐标系: F r 1. 一般情况下,功与力和路径有关 ∫∫ =⋅= b a b a d αdcos sFrFA r r 说明 ++≠ AAA zyx ∫∫ == b a b a t θdcosd sFsF

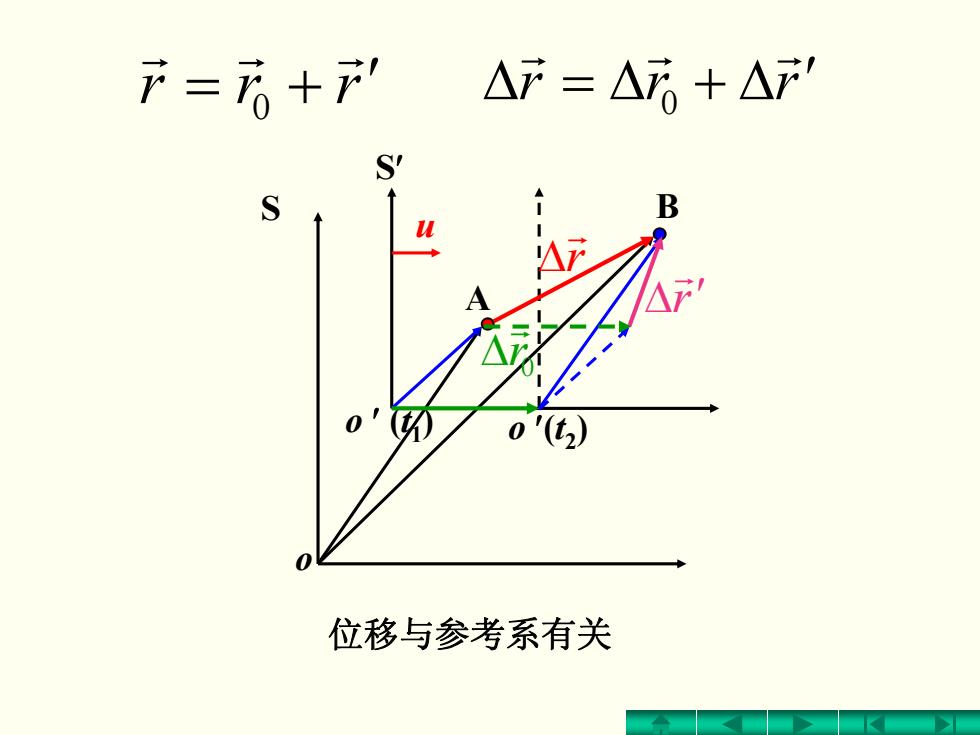
产=+ S' S 位移与参考系有关
= + rrr ′ r r r 0 位移与参考系有关 S S′ o o ′ A u 0r r r' r r r
产=+ △产=△+△F1 S' S W A 0 0 位移与参考系有关
S S′ o o ′ (t1) A B u o ′(t2) r r Δ Δr′ r = + rrr ′ r r r 0 Δ = Δ + Δrrr ′ r r r 0 0r r Δ 位移与参考系有关

3.合力的功等于各分力的功的代数和。 4=∑d∑心Ed=∑4 4.平均功率 P= △A △t 瞬时功率 P= d 下.d=下.寸 dt dt W(瓦特)=J/s
4. 平均功率 t A P Δ Δ = vF t rF r r r r ⋅= ⋅ = d 瞬时功率 d W(瓦特)=J/s 3. 合力的功等于各分力的功的代数和。 ∫ ∑ ⋅= ba i i rFA r r d)( = ∫ =⋅ ∑∑ i i i b a i ArF r r d t A P d d =

[例3-1)小球在水平变力F作用下缓慢移动,即在所有位 置上均近似处于力平衡状态,直到绳子与竖直方向成0角。 求:(1)F的功,(2)重力的功。 解:Fcos0=mg sin0F=ng tan0 F=mg tancos0=mgsine A,=∫F.d=∫Fds=mgsin6d0 mg mgl(1-cose) 变力 Ae=∫mg·dF=0-mg sin01d0 =-mgl(1-cose) 恒力曲线运动
F cosθ = mg sinθ t = mgF θ costan θ = mg sinθ ∫ mg ⋅= rgmA r r d 解: = mgF tanθ = −mgl − θ )cos1( F tdd sFrFA ∫∫ =⋅= r r = mgl − θ )cos1( 变力 恒力 曲线运动 [例3-1] 小球在水平变力 作用下缓慢移动,即在所有位 置上均近似处于力平衡状态,直到绳子与竖直方向成θ 角。 求:(1) 的功, (2) 重力的功。 F r F r m l θ θ F r gm r ∫ = θ θθ 0 lmg d sin ∫ −= θ θθ 0 lmg d sin

二、质点的动能定理 设质点m在力的作用下沿曲线从a点移动到b点 元功: d4=F.ds Fcosads dv Fcosa=ma =m dv d4=Fcosads=m ards mvdv dt 总功: A=∫dM=mdw=m时-f)=E6-R
二、质点的动能定理 =⋅= α dcosdd sFsFA r r t v F mma d d cos α t == s t v msFA d d d = α dcosd = 总功: ∫ ∫ == 2 1 dd v v vmvAA s 设质点 m在力的作用下沿曲线从 a点移动到 b 点 r d α F r b 1 a v r 2 v r 元功: = dvmv EEvvm kk ab 2 1 2 2 )( 2 1 −=−=

质点的动能定理: 合外力对质点所做的功等于质点动能的增量。 4=m-m=w- 说明 1.合外力的功是动能变化的量度。 A>0→Eb>Eka,A<0→Eb<Ea 2.A,E与参考系有关,动能定理只在惯性系中成立。 3.应用:A→△E 4微分形式:户.d=d近,F可= dEk dt
质点的动能定理: 合外力对质点所做的功等于质点动能的增量。 EEmvmvA kk ab 21 22 21 21 −=−= 0 , >→> EEA kk ab 说明 ⇔ ΔEA k 3. 应用: =⋅ ErF k ,dd 1. 合外力的功是动能变化的量度。 k 2. ,EA 与参考系有关,动能定理只在惯性系中成立。 r r t E vF d d k =⋅ r r 4. 微分形式: < 0 → < EEA kk ab