
第14章稳恒兹场 §14.1磁感应强度及洛仑兹力公式 §14.2毕奥一萨伐尔定律 §14.3磁高斯定理安培环路定理 §14.4磁场对载流导线的作用 §14.5带电粒子的运动
第 14 章 稳恒磁场 §14.1 磁感应强度 及洛仑兹力公式 §14.3 磁高斯定理 安培环路定理 §14.2 毕奥—萨伐尔定律 §14.4 磁场对载流导线的作用 §14.5 带电粒子的运动

§14.3磁高斯定理安培环路定理 一、磁通量 通过小面元磁通量 dΦn=Bcos@S=B.dS/ hn=八dD=j川Bcos =J八B.dS单位T-m2=wb 二、磁高斯定理 静电场高斯定理: fE.ds=qleo B.d5=?
§14.3 磁高斯定理 安培环路定理 一、磁通量 SBSB r r d ddcos m Φ = θ ⋅= ∫∫∫∫ == s s m dΦΦ θdcos SB 静电场高斯定理: ∫∫ =⋅ s qSE 0 /d ε r r ∫∫ =⋅ s SB ?d r r 二、磁高斯定理 通过小面元磁通量 WbmT 2 单位 =⋅ S r d θ n r S B r ∫∫ ⋅= s SBr r d

由毕奥一萨伐尔定律:dB=凸,d×F 4πr3 dΦ=0 任意电流系统可分为di,Idi,… 各自产生磁场 d8,dB2…1d 通过闭合面之磁通量d①,d中,… 通过闭合面之总磁通量 中nm=fB.dS=d+d中,+…=0
L r r d,d 21 lIlI L r r d,d BB 21 Φ d,d Φ 21 L L r r ++=⋅= m ∫∫ 21 Φ ddd ΦΦ S SB Φ = 0d 任意电流系统可分为 各自产生磁场 通过闭合面之磁通量 由毕奥—萨伐尔定律: 通过闭合面之总磁通量 3 0 d 4π d r rlI B r r r × = μ S = 0

E.ds=q/Eo B.d5-0 E线出自正电荷,收于负电荷 B线无头无尾 静电场为有源场! 磁场为无源场! 磁场与电场不同等的原因:自然界无磁单极 >狄拉克磁单极
∫∫ =⋅ s qSE 0 /d ε r r ∫∫ =⋅ S SB 0d r r E线出自正电荷,收于负电荷 r B线无头无尾 r 静电场为有源场! 磁场与电场不同等的原因:自然界无磁单极 ¾狄拉克磁单极 磁场为无源场!

三、安培环路定理 静电场: Ed7=0 无旋场 稳恒磁场: B.d7=? 有旋场 若任选一根磁力线为闭合回路 fB.di=fBdl≠0
三 、安培环路定理 静电场: ∫ =⋅ l lE 0d r r 稳恒磁场: =⋅ ?d ∫l lBr r 若任选一根磁力线为闭合回路 ∫ ⋅ l lBr r d ≠ 0 ∫ = l dlB 无旋场 ??? 有旋场

用长直电流的磁场来讨论: dl B.dI =Bdl cos=Brdo 2元 Bd-fnld 1绕向相反或电流反向, fB.di=-4,1
ϕ μ e r I B r r 2π 0 = =⋅ = BrlBlB dcosdd ϕθ r r I = μ0 l 绕向相反或电流反向, IlB l 0 d −=⋅ μ ∫ r r θ l r d r r dϕ l B r I l 用长直电流的磁场来讨论: ϕ μ ϕ d 2π dd 0 r rI BrlB∫∫∫ lll ==⋅ r r ∫ = l I ϕ μ d 2π0

fBd=BBd B -〔dw-人do。 N次链套:B.d7=-M4,1 如空间有多个电流,则: 手d1-到∑风小l∑:处在0回中的体流 =∑f月d)=4∑1
11 ddd 22 1 2 lBlBlBl l l r r r r r r ⋅+⋅=⋅ ∫ ∫ ∫ N次链套: INlB l ∫ d −=⋅ μ0 r r = ∑i i I μ0 ϕ 1 d l r 2 d l r B1 r B 2 r 2 l 1 l 如空间有多个电流,则: ∑i i lBlB I :处在积分回路中的电流 l i i l v v v v d ⎟⋅d ⎠ ⎞ ⎜ ⎝ ⎛ =⋅ ∫ ∫ ∑ ∑ ( ) ∫ ⋅= i l i lBv v d )dd( 2 π 1 2 0 ∫∫ = − l l I ϕϕ μ = 0

注意:1.代数和 B.d=4,4- 9 B由所有电流共同产生 但安培环路定理表达式中 的电流强度是指穿过闭合 曲线的电流,不包括闭合 曲线以外的电流。 2.上述讨论不是严格证明,只是说明。 3. fB.di≠0 磁场为有旋场! 电流是磁场的涡旋中心 4.仅适用稳恒电流产生的磁场
1. 代数和 IIlB 210 )(d l −=⋅ ∫ μ r r 2. 上述讨论不是严格证明,只是说明。 4. 仅适用稳恒电流产生的磁场 磁场为有旋场! 电流是磁场的涡旋中心 B由所有电流共同产生 r 3 I 3. ≠⋅ 0d ∫l lBr r 1I 2 I 但安培环路定理表达式中 的电流强度是指穿过闭合 曲线的电流,不包括闭合 曲线以外的电流。 注意:
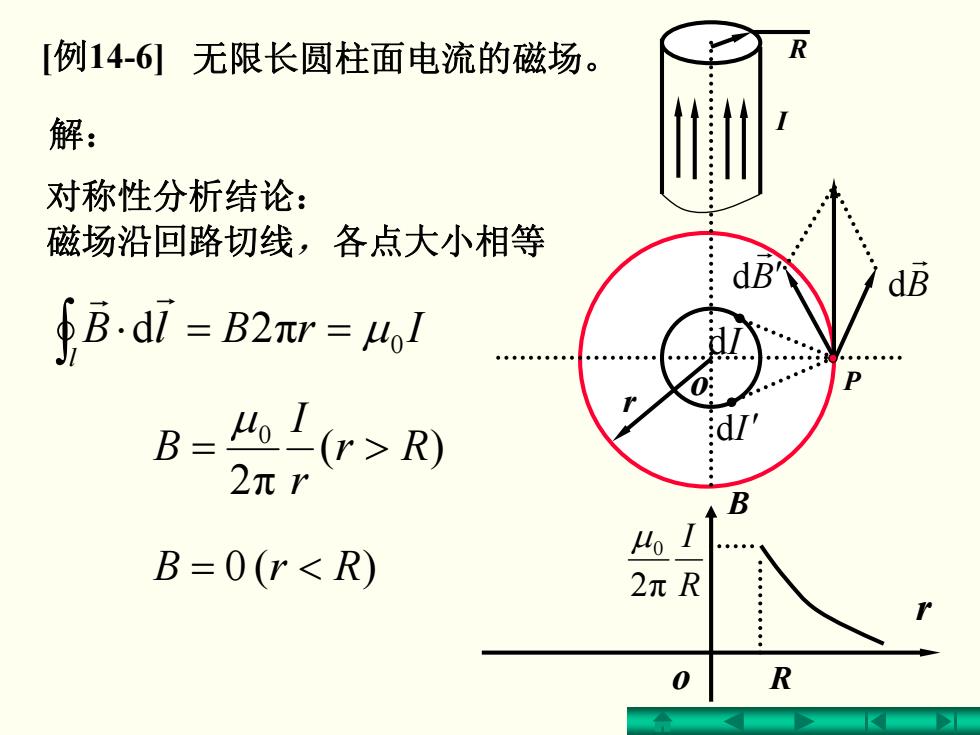
[例14-6]无限长圆柱面电流的磁场。 解: 对称性分析结论: 磁场沿回路切线,各点大小相等 dB B.d7 B2nr=ol B=4o(r>R) 2元r B B=0(r<R) 2πR 0 R
o R P B r B d ′ r d dI dI′ IrBlB l π 0 2 d ==⋅ μ ∫ r r r )( 2 π 0 Rr r I B >= μ = < RrB )( 0 I r B o R R I 2 π μ0 [ 例14-6] 无限长圆柱面电流的磁场。 解: 对称性分析结论: 磁场沿回路切线 ,各点大小相等
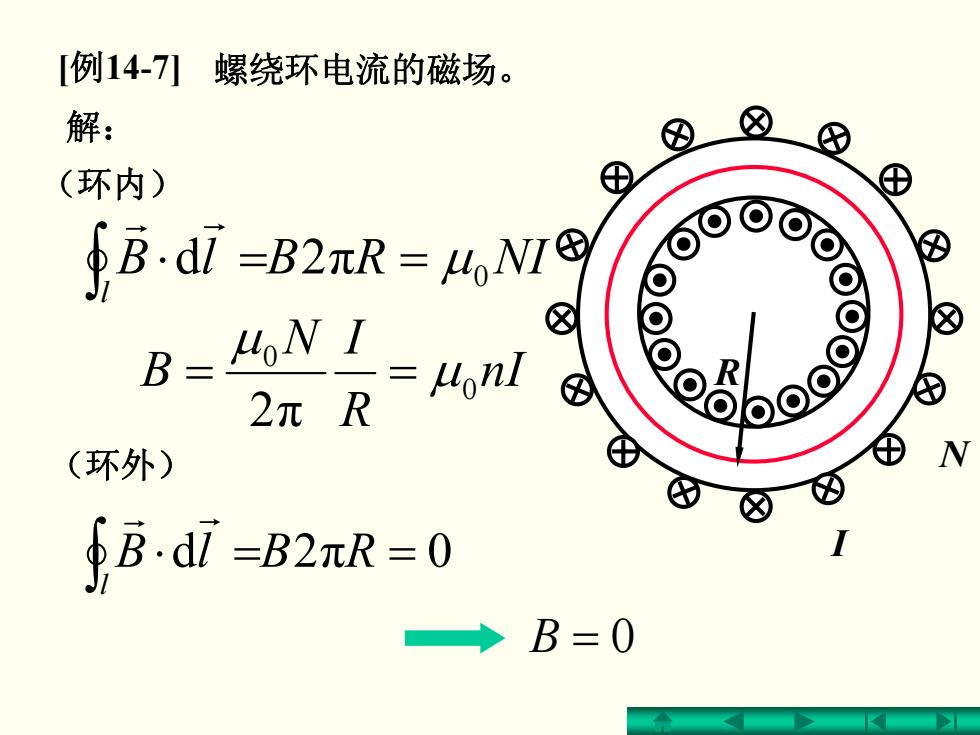
[例14-7] 螺绕环电流的磁场。 解: (环内) ⊕ fBd-B2xR-MoNt B=HoN I uonl 2元R (环外) fB.d=B2πR=0 ◆B=0
NIRBlB l π 0 2d ==⋅ μ ∫ r r nI R N I B 0 0 2 π μ μ == 2d π ==⋅ 0 ∫ RBlB l r r B = 0 (环外) (环内) R I N 解: [ 例14-7] 螺绕环电流的磁场