
第14拿稳恒磁场
第 14 章 稳恒磁场

第14章稳恒磁场 §14.1磁感应强度 及洛仑兹力公式 §14.2毕奥一萨伐尔定律 §14.3磁高斯定理安培环路定理 §14.4磁场对载流导线的作用 §14.5带电粒子的运动
第 14 章 稳恒磁场 §14.1 磁感应强度 及洛仑兹力公式 §14.3 磁高斯定理 安培环路定理 §14.2 毕奥—萨伐尔定律 §14.4 磁场对载流导线的作用 §14.5 带电粒子的运动
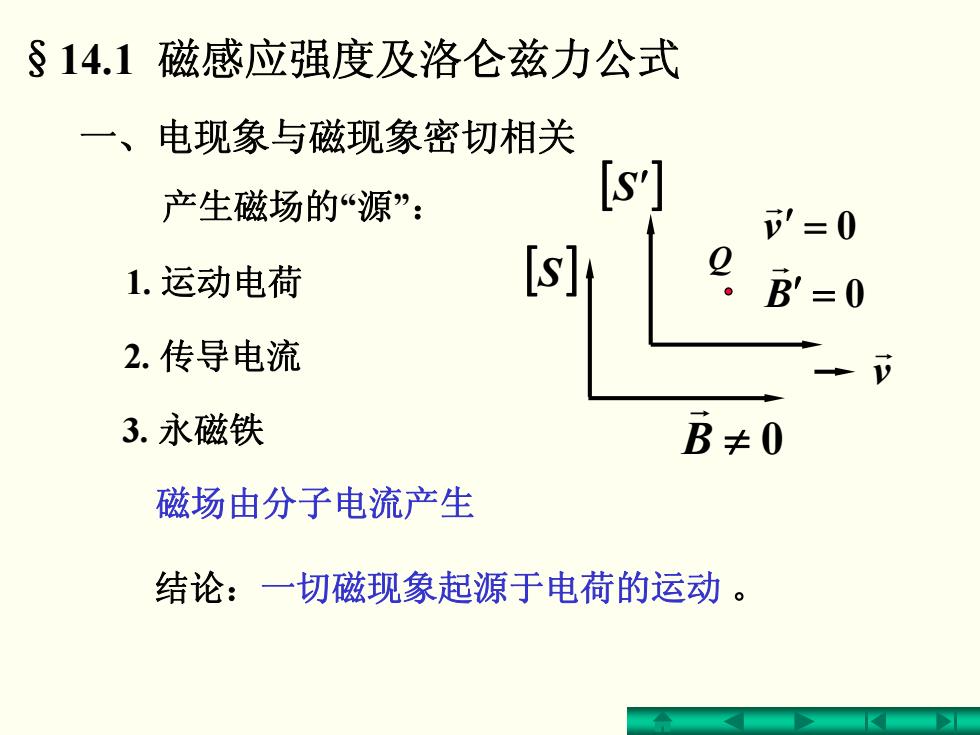
§14.1磁感应强度及洛仑兹力公式 一、电现象与磁现象密切相关 产生磁场的“源”: [s] =0 1.运动电荷 [s] 9B=0 2.传导电流 3.永磁铁 B≠0 磁场由分子电流产生 结论:一切磁现象起源于电荷的运动
§14.1 磁感应强度及洛仑兹力公式 一、电现象与磁现象密切相关 产生磁场的“源”: 1. 运动电荷 2. 传导电流 3. 永磁铁 磁场由分子电流产生 结论:一切磁现象起源于电荷的运动 。 v r Q [S′] 0 0 ′ = ′ = B v r r [S] B ≠ 0 r

二、磁场的描述 根据运动电荷或载流导线或小磁针在磁场 中受力情况来描述磁场。 实验结论: 1.=0则F=0,立≠0一般F≠0, 但(p点)沿某特定直线运动,则,F=0 规定B∥该直线(零磁力线) 2.F1立,F1B. 即F⊥下,B构成之平面。 9→-9→F→-Fx
FFqq r r −→⇒−→ F = 0 根据运动电荷或载流导线或小磁针在磁场 中受力情况来描述磁场。 r 但( p点)沿某特定直线运动,则 , r 规定 B p // 该直线(零磁力线) BvF r r r 即 ⊥ , 构成之平面。 BFvF . , r r r r 2. ⊥⊥ F ≠ 0 实验结论: 二、磁场的描述 r v = 0 r F = 0 r v ≠ 0 r 1. 则 , 一般 , x z y q p F r θ B r v r o

3.规定:F∥gD×B y 4.Fgvsine F gv sin 0 与q,y,B无关,只与位置有关。 F 规定:B= gv sin 0 SI中B之单位为T(特斯拉) 1T=1N/(A·m)
⋅ )mA/(1N=1T ∝ qvF sin θ r 4. qv sin θ F r 与 vq ,, θ 无关,只与位置有关。 qv sin θ F 规定: B = SI 中 B 之单位为 T (特斯拉) BvqF r r r 3. 规定: // × x z y q p F r θ B r v r o

F 总结:B之大小为 qvsinθ 方向沿零磁力线,且使F/∥g下×B 由于qT×月=qvBsin0=F 故F=q巾×B洛仑兹力公式
总结: 之大小为 B r qv sin θ F 方向沿零磁力线,且使 BvqF r r r // × =× qvBBvq sin θ = F r r 由于 BvqF r r r 故 ×= 洛仑兹力公式

二、带电粒子在匀强磁场中的运动 (1)V/∥B→F=0 >粒子运动状态不变! (2) ⊥B→F=qvB qvB = R mv R= gB 2元R 2元m T= >粒子沿圆周运动! V gB
R mv qvB 2 = qB mv R = qB m v R T 2π 2 π == =→⊥ qvBFBv r r (2) 二、带电粒子在匀强磁场中的运动 (1) // FBv =→ 0 ¾粒子运动状态不变! r r ¾粒子沿圆周运动!
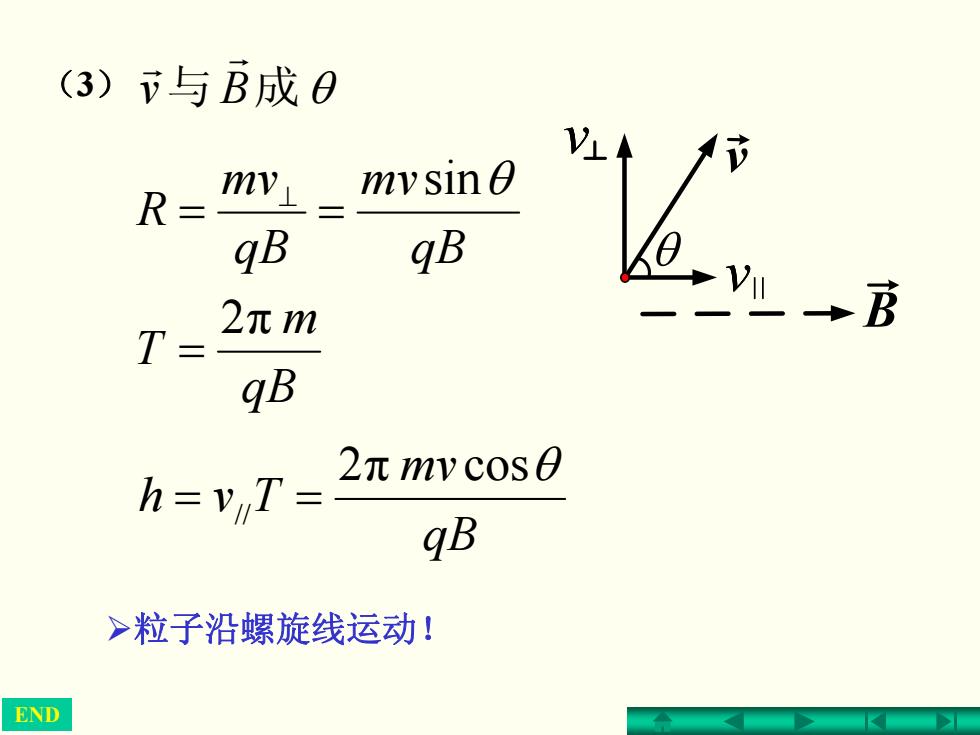
(3)与B成0 R= mv mvsin gB qB T= 2元m gB h=v T= 2πmvc0s0 gB >粒子沿螺旋线运动! END
qB mv qB mv R sinθ == ⊥ END qB m T 2π = qB mv Tvh 2π cos θ // == Bv 成与 θ r r (3) ¾粒子沿螺旋线运动!