
第22章量子力学基础 §22.1实物粒子的波动性 §22.2波函数及统计解释 §22.3不确定性关系 §22.4薛定谔方程 §22.5力学量算符的本征值问题 §22.6薛定谔方程的应用 §22.7氢原子量子理论 §22.8电子的自旋泡利不相容原理
§22.1 实物粒子的波动性 §22.2 波函数及统计解释 §22.3 不确定性关系 §22.4 薛定谔方程 §22.6 薛定谔方程的应用 §22.5 力学量算符的本征值问题 §22.7 氢原子量子理论 §22.8 电子的自旋 泡利不相容原理 第 22 章 量子力学基础

§22.7氢原子量子理论 氢原子中的电子在中心力场中运动 Ur)=- e2 4元8' 2+U 2m 采用球坐标系 h2 1 6 2 2mr20r' +U(r)
§22.7 氢原子量子理论 氢原子中的电子在中心力场中运动 U m H +∇−≡ 2 2 2 ˆ h r e rU 0 2 4π )( ε −= )( 2 ˆ 1 2 ˆ 2 2 2 2 2 rU mr L r r rrm H ⎟ ++⎠⎞ ⎜⎝⎛ ∂∂ ∂∂ −= h 采用球坐标系

其中2为电子绕核的轨道角动量平方算符 L,的为轨道角动量在方向的分量: ∂ L:=-ih 一、角动量算符的本征值问题 通过求解2和,的本征方程得到本征函数和本征 值如下(过程略):
θθ θ θθ 2 2 2 2 sin ˆ sin sin ˆ Lz L ⎟ +⎠⎞ ⎜⎝⎛ ∂∂ ∂∂ −= h ∂ϕ ∂ −= ih ˆ L z 一、角动量算符的本征值问题 其中L2为电子绕核的轨道角动量平方算符 Lz的为轨道角动量在z方向的分量: 通过求解L2和Lz 的本征方程得到本征函数和本征 值如下(过程略):
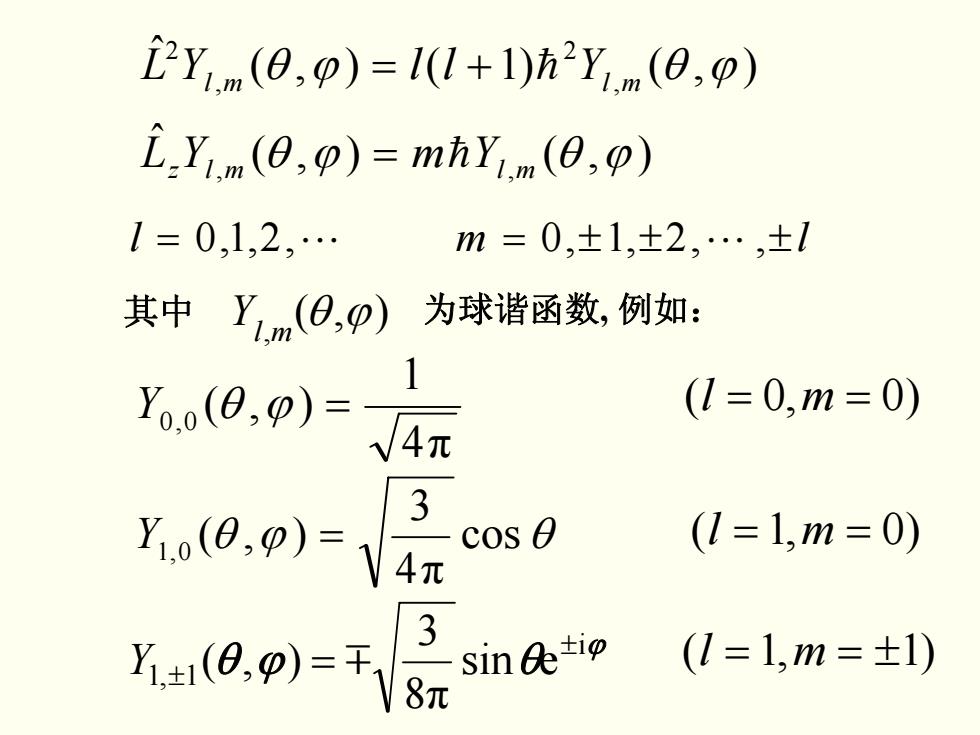
2Ym(0,p)=1(1+1)h2Y.m(0,p) i.Y,m(0,p)=mhY.m(0,p) 1=0,1,2,… m=0,±1,±2,…,±l 其中Ym(O,p)为球谐函数,例如: Yo.0(8,p)= (1=0,m=0) 3 Y(0,p)=4元 cos 0 (1=1,m=0) 3 Y±(8,p)=干 sin ti (1=1,m=±1) 8元
l = ,2,1,0 L m = ± ± L ,,2,1,0 ±l ),()1(),( ˆ , 2 , 2YL ml ϕθ += h Yll ml ϕθ ),(),( ˆ YL ,mlz ϕθ = hYm ,ml ϕθ 其中 ),( , θ ϕ ml Y 为球谐函数, 例如: 4π 1 ),( Y 0,0 ϕθ = = ml = )0,0( = ml = )0,1( = ml = ± )1,1( ϕθ cos θ 4π3 ),( Y 0,1 = ϕ ϕθ θ i 1,1 esin 8π3 ),( ± Y ± = m

1.主要结论 ·和L,有共同的本征函数Y,m(O,p) 。的本征值为 L2=1(1+1)h2 =0,1,2..称为角量子数。 角动量的大小:L=V√1(1+1)方 =0,√2h,V6h, 角动量L的取值是量子化的(量子力学很自然地给出角 动量的量子化),最小值可取零(与玻尔假设不同)
llL += )1( h 角动量L的取值是量子化的(量子力学很自然地给出角 动量的量子化),最小值可取零(与玻尔假设不同)。 1. 主要结论 • 和 有共同的本征函数 Yl, m(θ,ϕ) 2 Lˆ Lz ˆ • 的本征值为 2 Lˆ 2 2 llL += )1( h l=0,1,2… 称为角量子数。 角动量的大小: = hh ,...6,2,0

·可能的本征值取 L.=mh m=-,-l+1,.,l-1,1称为磁量子数。 L=0,±h,士2h,.,±1h 角动量在空间的取向也是量子化的。 对于一定的角量子数1,磁量子数m可取(2l+1)个值, 角动量在空间z方向的取向只有(21+1)种可能
z = mL h m=-l,-l+1,…,l-1,l 称为磁量子数。 • L ˆ z可能的本征值取 角动量在空间的取向也是量子化的。 Lz = ± ± , ,...2 , ,0 ± lhhh 对于一定的角量子数l ,磁量子数 m 可取(2 l +1)个值, 角动量在空间 z 方向的取向只有(2 l +1)种可能
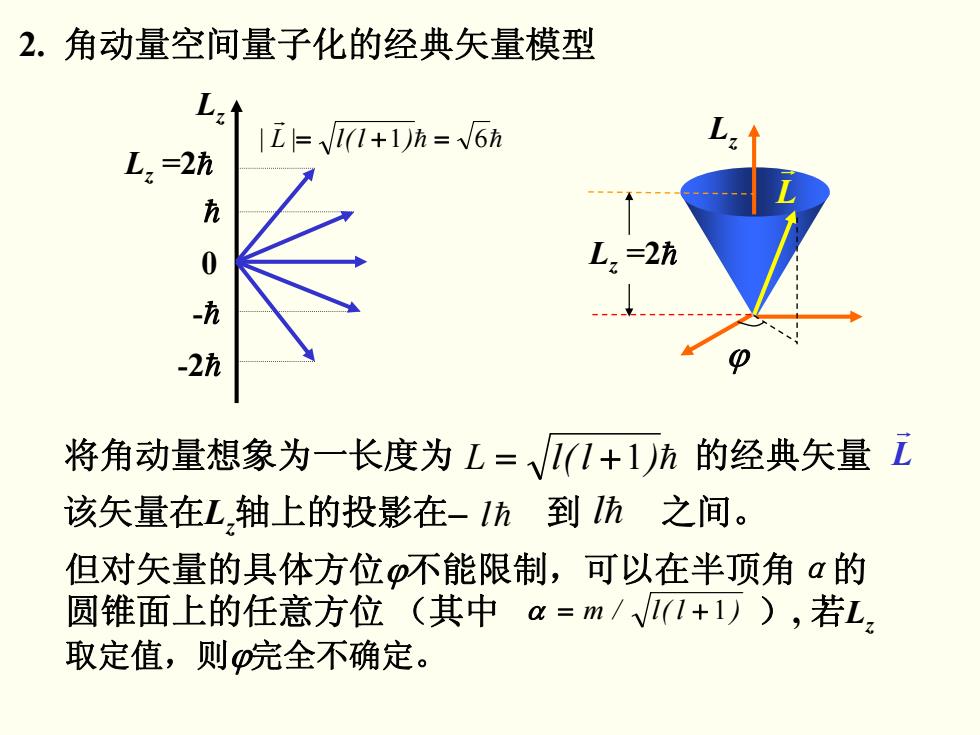
2.角动量空间量子化的经典矢量模型 L:t 1i=√11+1)h=V6方 L,=2h 0 L.=2h -2h 将角动量想象为一长度为L=V(1+1)h的经典矢量 该矢量在L,轴上的投影在-1h到h之间。 但对矢量的具体方位p不能限制,可以在半顶角α的 圆锥面上的任意方位(其中a=m/V(1+1)),若L, 取定值,则完全不确定
2. 角动量空间量子化的经典矢量模型 该矢量在Lz轴上的投影在 到 之间。 − lh lh 但对矢量的具体方位ϕ不能限制,可以在半顶角α的 圆锥面上的任意方位 (其中 ), 若Lz 取定值,则ϕ完全不确定。 α = + 1 )l(l/m hh r )l(l|L| =+= 61 0 -2h h Lz =2h -h Lz 将角动量想象为一长度为 += 1)l(lL h 的经典矢量 Lr Lz Lz =2h ϕ L r

注:以上矢量模型完全是为了使角动量空间取向量子 化的描述更形象,是一种辅助方法。 量子理论中由于测不准关系的限制,电子绕原子核 的角动量方向在任何时刻均是不确定的。 3.Zeeman效应证明角动量空间取向的量子化 氢原子从第一激发态(=1)跃迁到基态(=0)时,发 射光谱只有一条谱线。 但在外磁场中发现,该条谱线分裂为三条。 =1 对应 对应 B=O时光谱线 B0时光谱线
注:以上矢量模型完全是为了使角动量空间取向量子 化的描述更形象,是一种辅助方法。 量子理论中由于测不准关系的限制,电子绕原子核 的角动量方向在任何时刻均是不确定的。 3. Zeeman效应证明角动量空间取向的量子化 氢原子从第一激发态( l=1)跃迁到基态( l=0)时,发 射光谱只有一条谱线。 但在外磁场中发现,该条谱线分裂为三条。 B= 0时光谱线 l=1 l=0 对应 对应 B ≠0时光谱线 l=1 l=0

称光谱这种分裂现象为塞曼效应。 解释:电子的轨道角动量对应于轨道磁矩 e i1= 2mo 在外磁场中电子的轨道磁矩具有的附加磁能为: AE=-,·B=e元B ehB (m=-1) 2mo L.B=m eh B= 0 (m=0) 2mo 2m0 ehB (m=1) 2mo 由于电子轨道角动量空间取向的量子化,氢原子的能级 在外加磁场出现了分裂现象,进一步导致谱线的分裂
L m e l r r 0 2 μ −= 电子的轨道角动量对应于轨道磁矩 称光谱这种分裂现象为塞曼效应 。 在外磁场中电子的轨道磁矩具有的附加磁能为: l BE r r μ ⋅−=Δ BL m e z 0 2 = BL m e r r ⋅= 2 0 B m e m ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ = 2 0 h ⎪ ⎪ ⎩ ⎪ ⎪ ⎨ ⎧ = = − −= = )1( 2 )0( 0 )1( 2 0 0 m m Be m m m Be h h 由于电子轨道角动量空间取向的量子化,氢原子的能级 在外加磁场出现了分裂现象,进一步导致谱线的分裂。 解释:

1902诺贝尔物理学奖得主 塞曼 塞曼效应的 发现和研究
1902诺贝尔物理学奖得主 塞曼 塞曼效应的 发现和研究