
第13章电介质 §13.1静电场中的电介质 §13.2介质中的高斯定理 §13.3介质边界两侧的静电场 §13.4静电场的能量
第 13 章 电介质 §13.2 介质中的高斯定理 介质中的高斯定理 §13.1 静电场中的电介质 静电场中的电介质 §13.4 静电场的能量 §13.3 介质边界两侧的静电场 介质边界两侧的静电场
§13.3介质边界两侧的静电场 本节讨论极靠近边界两侧D或E之间的关系。 一、场强与界面垂直 设界面没自由电荷 -DAS+D,AS=fD.dS-0 D,=D, ◆E,=E,E, D线连续 E线中断
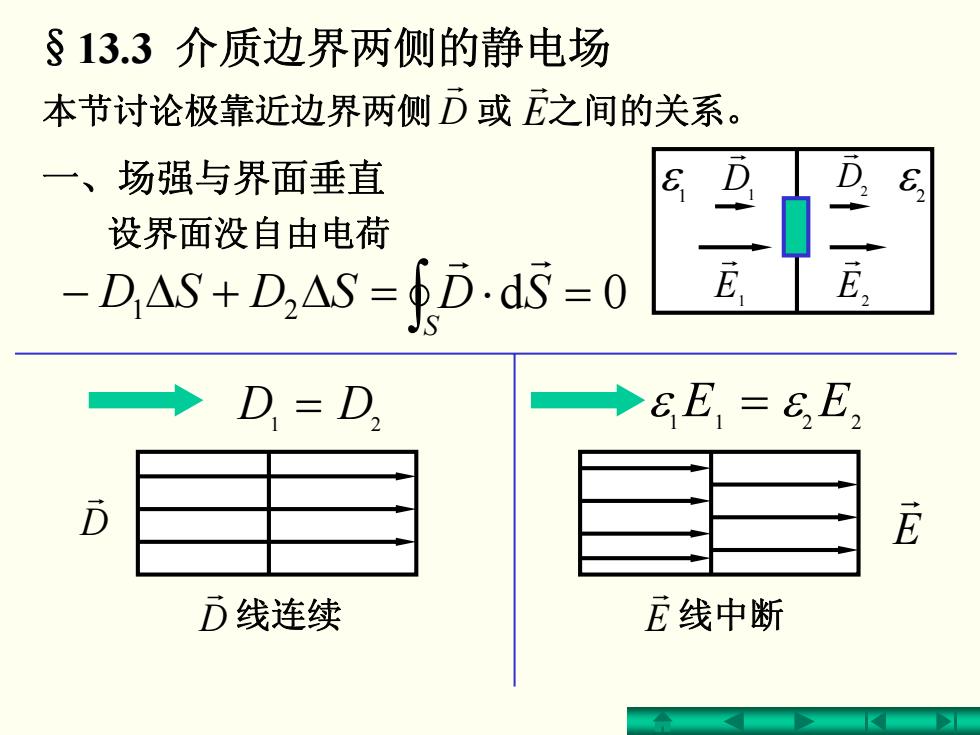
ε 1 ε 2 §13.3 介质边界两侧的静电场 本节讨论极靠近边界两侧 或 之间的关系。 r D r E 一、场强与界面垂直 rD1 rD2 r E1 r =⋅ 0d E2 ∫S SDr r 设界面没自由电荷 D D 1 2 = ε ε 11 2 2 E E = r D E r r D 线连续 rE 线中断 − 1Δ + 2ΔSDSD =
二、场强与界面斜交 利用介质中的高斯定理: -D cosAS+D,cose,AS=0 →Dn=Dn →6E1n=62E2n 利用环流定理: E, ■■■ E,sine Al+E,sine△M=0 →E1t=E2 tan O tan O, 82 一-%
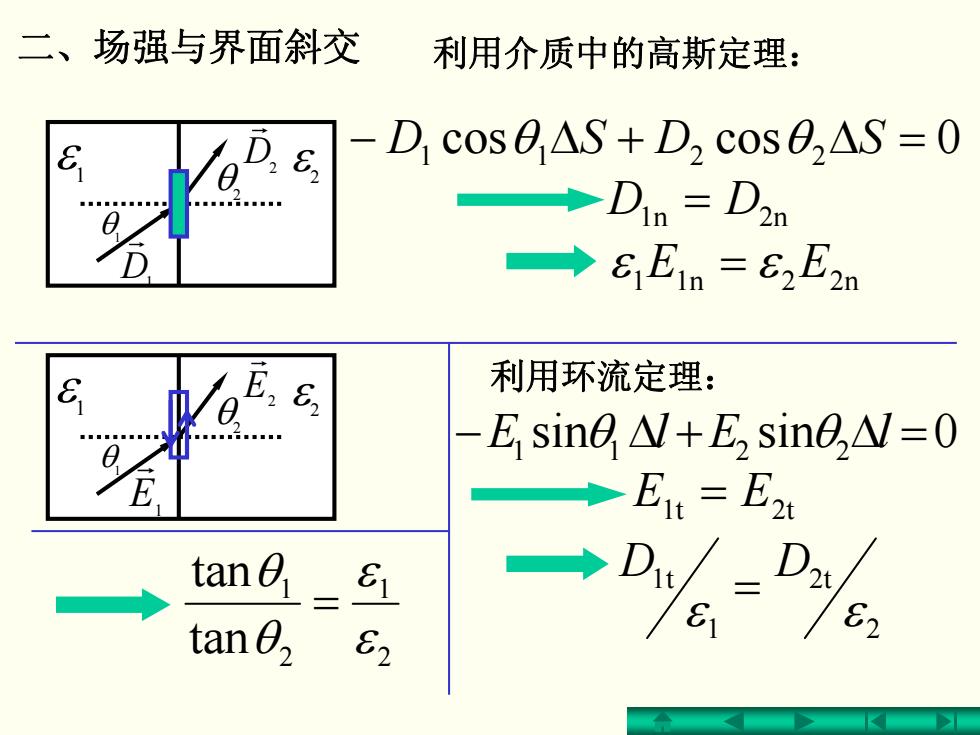
ε 1 ε 2 θ1 θ2 r E1 r E2 ε 1 ε 2 θ1 θ2 r D1 r D2 二、场强与界面斜交 − cosθ11 Δ + cosθ 22 ΔSDSD = 0 1n = DD 2n sinθ θ2211 lElE =Δ+Δ− 0sin 1t = EE 2t EE 2n21n1 ε = ε 2 2t 1 t1 εε DD = 利用环流定理: 利用介质中的高斯定理: 2 1 2 1 tan tan ε ε θ θ =
「例题13-31如图示系统,求(1)电荷分布;(2)电场分 布,(3)电容器电容。 解:定性分析 (1)由对称性,电荷上下各为均匀分布; (2)由静电平衡条件: 电场强度沿径向 (不然,电荷会继续移动); (3)由边界条件:介面两侧电场强度的切向分量相等, Et=E 而电场强度沿径向, →E1=E2=E(r)e, (两侧的电位移矢量则不相同!) (两部分的导体表面电荷密度不同!)
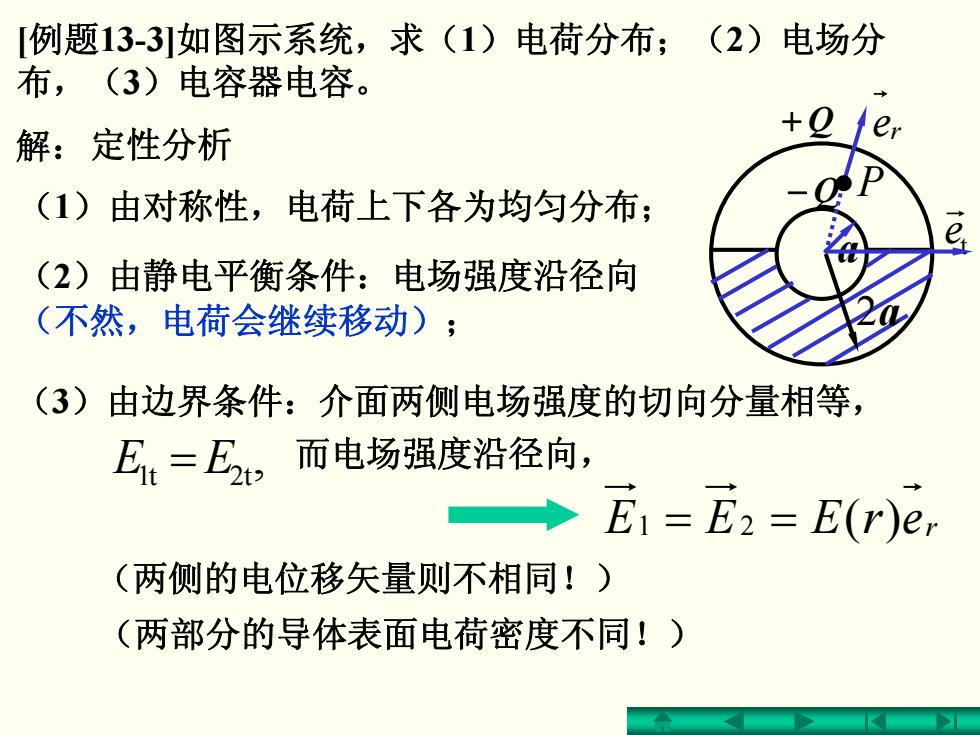
[例题13-3]如图示系统,求(1)电荷分布;(2)电场分 布,(3)电容器电容。 + Q − Q a 2a 解:定性分析 (1)由对称性,电荷上下各为均匀分布; (2)由静电平衡条件:电场强度沿径向 (不然,电荷会继续移动); (3)由边界条件:介面两侧电场强度的切向分量相等, , =EE 2tt1 21 == )( erEEE r 而电场强度沿径向, (两侧的电位移矢量则不相同!) (两部分的导体表面电荷密度不同!) t e r er •P

利用高斯定理: D,)2m-2+D,r22=fD.dS=-0+0 8网 →8E(r)2π2+6o8,E(r)2πr2=- ◆E(r)= -O 2π6(1+6)r2 极化电荷分布可由O=o&E(r)求得。 电容器电容可由电容定义求得。 END
利用高斯定理: QSDS −=⋅ ∫ d )()(1 0 = ε rErD )()(2 r0 = ε ε rErD 和: + −= QrrErrE 2 r0 2 ε 0 2)( π εε 2)( π 2 r0 2π )1( )( r Q rE + εε − = 极化电荷分布可由σ = ε ε r0 rE )( 求得。 电容器电容可由电容定义求得。 END S + =2 2 2 1 2)( π 2)( πrrDrrD + Q − Q a 2a