
第14章稳恒磁场 §14.1磁感应强度及洛仑兹力公式 §14.2毕奥一萨伐尔定律 §14.3磁高斯定理安培环路定理 §14.4磁场对载流导线的作用 §14.5带电粒子的运动
第 14 章 稳恒磁场 §14.1 磁感应强度 及洛仑兹力公式 §14.3 磁高斯定理 安培环路定理 §14.2 毕奥—萨伐尔定律 §14.4 磁场对载流导线的作用 §14.5 带电粒子的运动
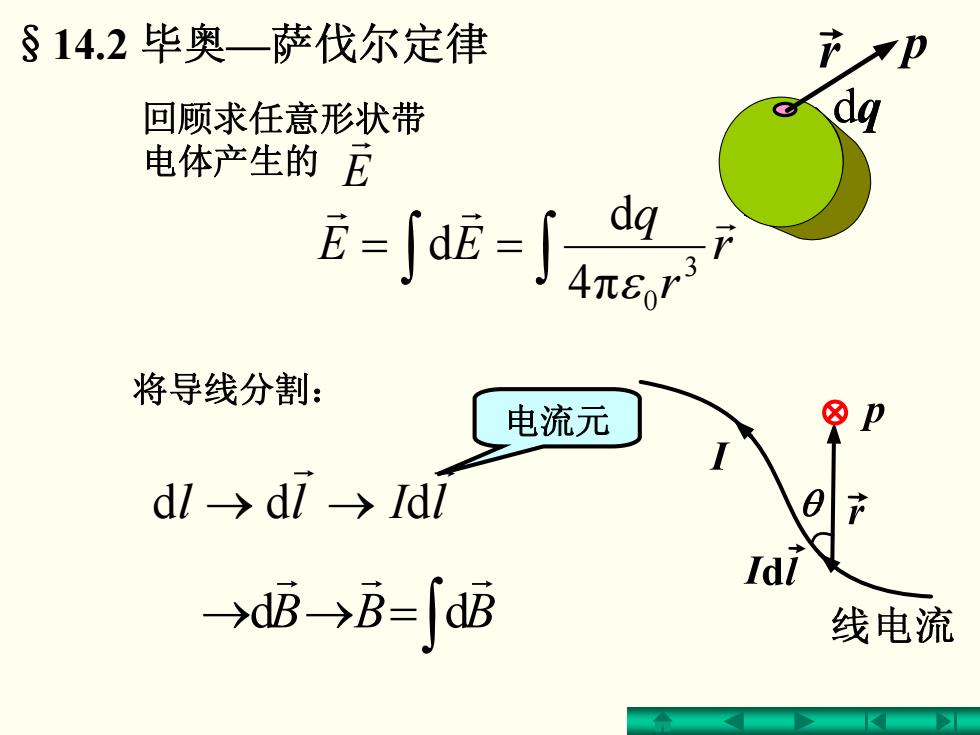
§14.2毕奥一萨伐尔定律 回顾求任意形状带 dq 电体产生的 f=a-ag 将导线分割: 电流元 dl→di>ldi Idl →B→B=∫dB 线电流
∫ ∫ == r r q EE r r r 3 π 0 4 d d ε lIll r r →→ ddd r E 回顾求任意形状带 电体产生的 §14.2 毕奥—萨伐尔定律 将导线分割: 电流元 ∫ =→→ BBBr r r dd
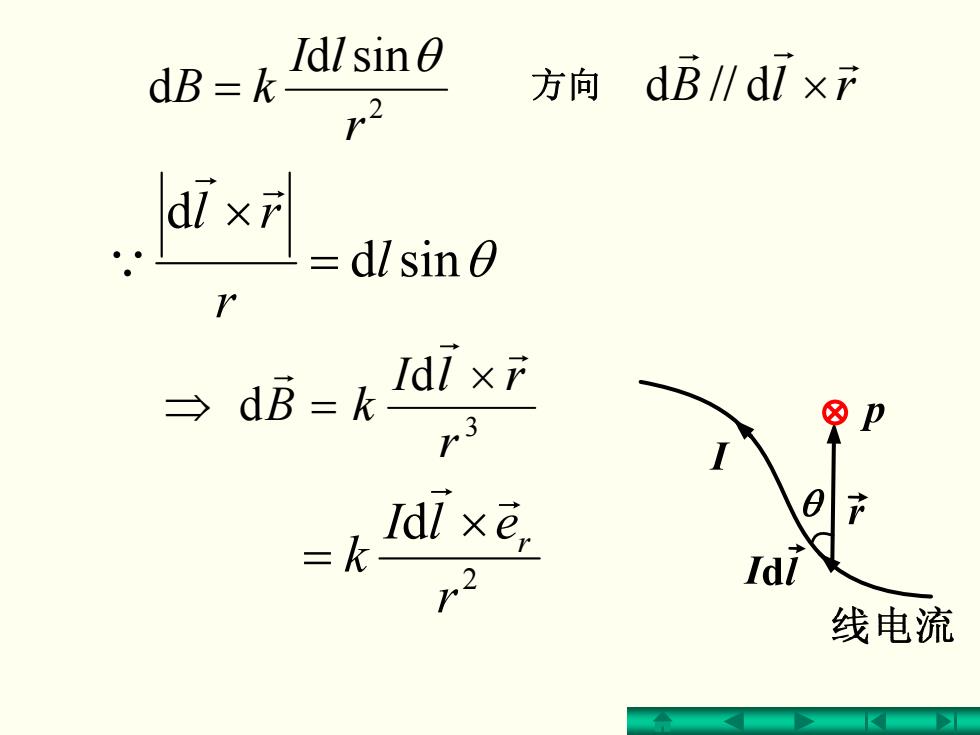
dB=k Idl sin 方向dB∥dixF 2 ldix dlsin 0 三dB=k dl×r Idi×e, Idl 线电流
2 sind d r lI kB θ = sind θ d l r rl = × r r Q 3 d d r rlI kB r r r × =⇒ rlB r r r 方向 d//d × 2 d r elI k r r r × =

dB=k 2 sI制中k=4 4=4π×10-7T.m/A 真空磁导率 Idl产生磁场之B线
2 3 d d d r rlI k r elI kB r r r r r r × = × = 4π = μ0 SI 制中 k 4π m/A T10 7 0 ⋅×= − μ lI r d Br 产生磁场之 线 真空磁导率

[例14-1刂直流电的磁场。 解: 每个电流元产生磁场同方向 =a0=,m0 2 z=-d cote Id d dz d0 sin20 d r= sin 0
[例14-1] 直流电的磁场。 2 0 sind 4π d r zI BB μ θ ∫ ∫ == = −dz cotθ θ θ d sin d 2 d z = sinθ d r = z o d z θ 1 θ 2 zI r d 1 z 2 z r r p θ 解: 每个电流元产生磁场同方向

Mo re Isine do B= 7 4元 d2 sin20 sin20 41 sin 4a月-as8)
θ θ θ μ θ θ θ 2 2 2 0 sin d sin sin 4 π 2 1 ∫ = d I B θθ μ θ θ dsin 4 π 2 1 0 ∫ = d I )cos(cos 4 π 1 2 0 θθ μ = − d I z o d z θ 1 θ 2 zI r d 1 z 2 z r r p θ

特例:无限长 B=- (cose-cose2) 0,→0 02-→元 B= 41 2πd
特例:无限长 π 0 2 1 → → θ θ d I B 2π μ0 = θ1 θ2 p )cos(cos 4π 1 2 0 θθ μ = − dI B
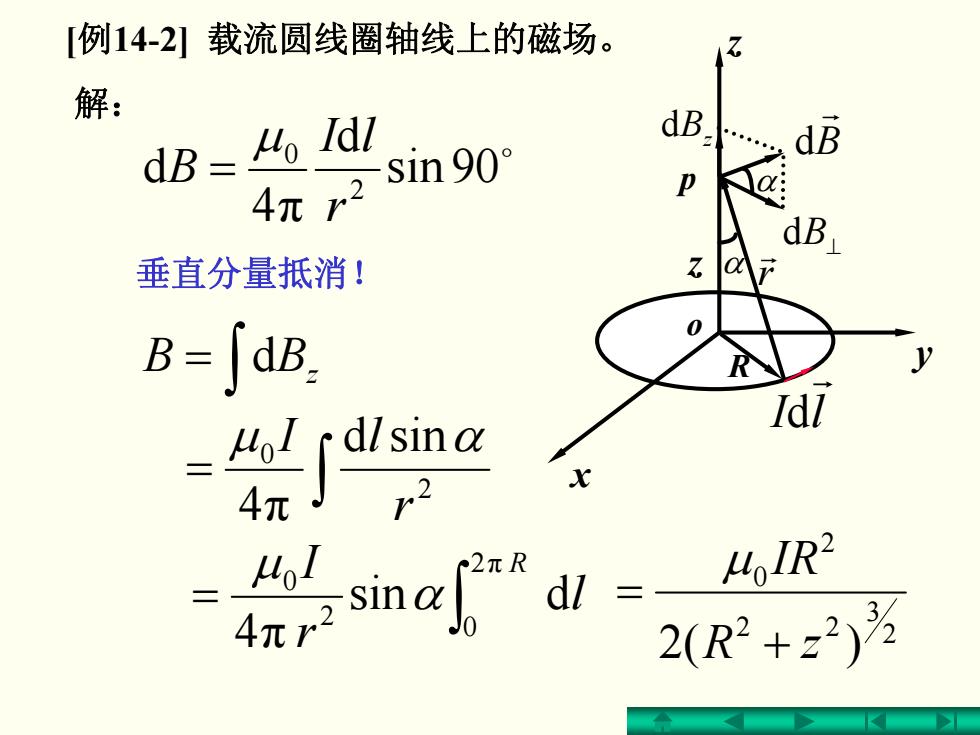
「例14-2】载流圆线圈轴线上的磁场。 解: dB=to Idl dB dB 4π2 sn909 dB 垂直分量抵消! 0 B=∫dB Idl 4,IR2 2(R2+z3)3
o 90sin d 4π d 2 0 r lI B μ= ∫ = BB z d ∫ = 2 0 sind 4π r μ I l α ∫ = R l rI 2π 0 2 0 d sin 4π α μ 23 22 2 0 zR )(2 IR+ = μ [例14-2] 载流圆线圈轴线上的磁场。 解: 垂直分量抵消! y x z R o p α α lI r d z rr dB⊥ B r z d dB
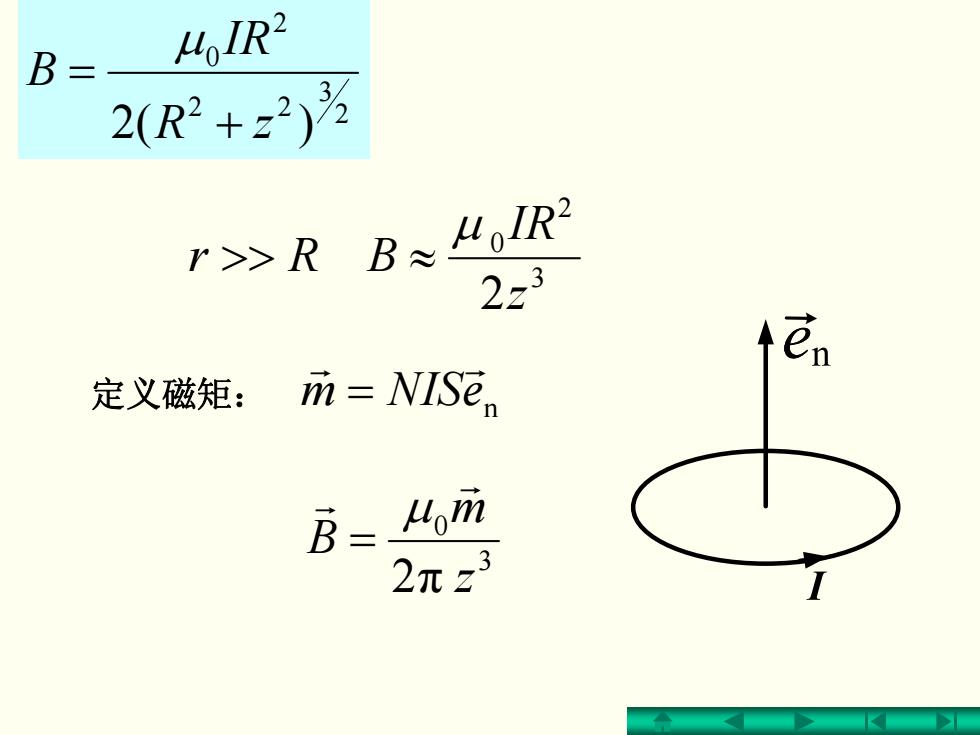
B 、 HoIR2 2(R2+232)为 r>>RB≈ oIR2 2z3 定义磁矩: m=NISe. B= om 2元z3
3 2 0 2z IR BRr μ≈>> n eNISmr r = 3 0 2π z m B r r μ = 2 3 22 2 0 zR )(2 IR B + = μ 定义磁矩:

[例14-3】螺线管产生的磁场。 B=、 HoIR2 解:一个薄片相当于一个载流圆线圈 2(R2+22)为 dB,=-Mo'nldx 2(R2+x2)3 X2 X 片-, 2(R2+x2)3 =4,(cosB,-c0s)利用x=Rcot0
2 3 22 2 0 )(2 d d xR xnIR Bp + = μ ∫ + = 2 1 2 3 22 2 0 )(2 x d x p xR xnIR B μ (cos )cos 2 2 1 0 ββ μ= − nI 2 3 22 2 0 zR )(2 IR B + = [例14-3] 螺线管产生的磁场。 μ 解: 利用 Rx cot= β 一个薄片相当于一个载流圆线圈