
第12章导体电学
第 12 章 导体电学

引 言 >静电场与物质的相互作用问题:(1)物 质在静电场中要受到电场的作用,表现出 宏观电学性质;(2)物质的电学行为也会 影响电场分布,最后达到静电平衡状态。 >理论基础为静电场的高斯定理与环流定理。 9. Ed5子9 80 Ed7=0
¾理论基础为静电场的高斯定理与环流定理。 ¾静电场与物质的相互作用问题:(1)物 质在静电场中要受到电场的作用,表现出 宏观电学性质;(2)物质的电学行为也会 影响电场分布,最后达到静电平衡状态。 0 d ε ∑ ∫ =⋅ i i S q SEr r =⋅ 0d ∫L lEr r 引 言

**物质分类** √导体 ·导体内存在大量的自由电子(在晶格离 子的正电场背景下)。 ·导体电中性与带电一与导体内部自由电 子是否多余或缺乏有直接的关系。 √绝缘体 ·与导体相对,绝缘体内没有可自由移动的 电子一电介质。 √半导体 ·半导体内有少量的可自由移动的电荷。 导体、电介质和半导体与静电场作用的物理 机制各不相同本章讨论金属导体
9导体 ***物质分类*** 9绝缘体 • 导体内存在大量的自由电子(在晶格离 子的正电场背景下)。 • 导体电中性与带电——与导体内部自由电 子是否多余或缺乏有直接的关系。 • 与导体相对,绝缘体内没有可自由移动的 电子——电介质。 导体、电介质和半导体与静电场作用的物理 机制各不相同。本章讨论金属导体。 9半导体 • 半导体内有少量的可自由移动的电荷

第12章导体电学 §12.1导体的静电平衡性质 §12.2空腔导体 §12.3电容及电容器 §12.4传导电流 §12.5电源及稳恒电流
第 12 章 导体电学 §12.1 导体的静电平衡性质 导体的静电平衡性质 §12.2 空腔导体 §12.3 电容及电容器 §12.4 传导电流 §12.5 电源及稳恒电流 电源及稳恒电流
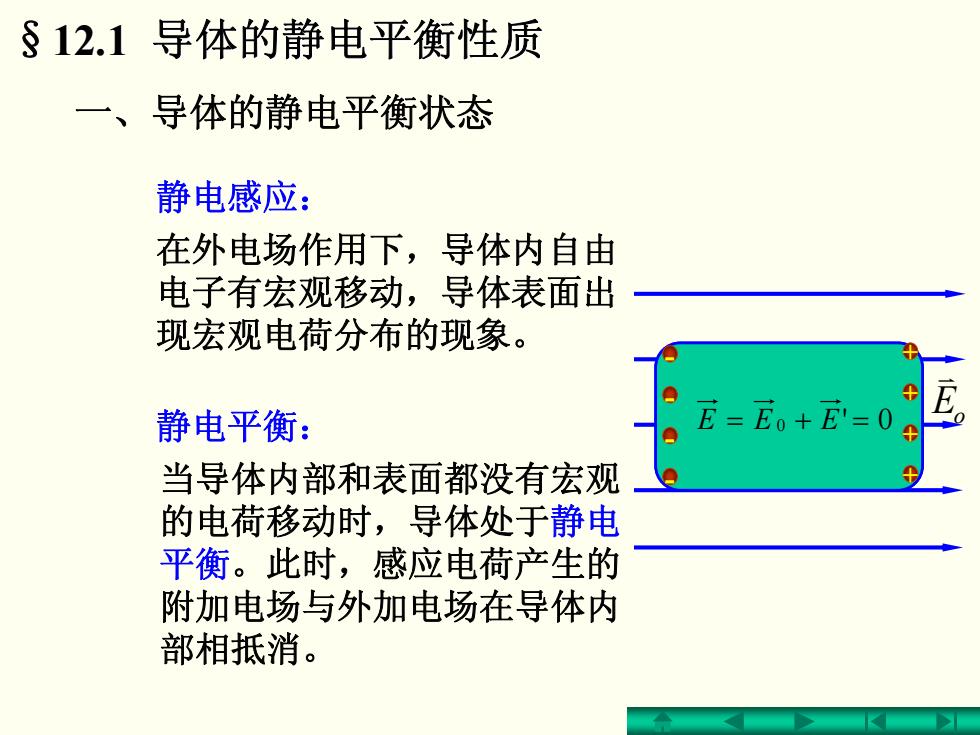
§12.1导体的静电平衡性质 一、 导体的静电平衡状态 静电感应: 在外电场作用下,导体内自由 电子有宏观移动,导体表面出 现宏观电荷分布的现象。 静电平衡: ● E=E0+E=0 当导体内部和表面都没有宏观 的电荷移动时,导体处于静电 平衡。此时,感应电荷产生的 附加电场与外加电场在导体内 部相抵消
§12.1 导体的静电平衡性质 导体的静电平衡性质 静电感应: 在外电场作用下,导体内自由 电子有宏观移动,导体表面出 现宏观电荷分布的现象。 一、导体的静电平衡状态 静电平衡: 当导体内部和表面都没有宏观 的电荷移动时,导体处于静电 平衡。此时,感应电荷产生的 附加电场与外加电场在导体内 部相抵消。 Eo v F - E′ v - + + + + + - - - - 0 EEE =+= 0
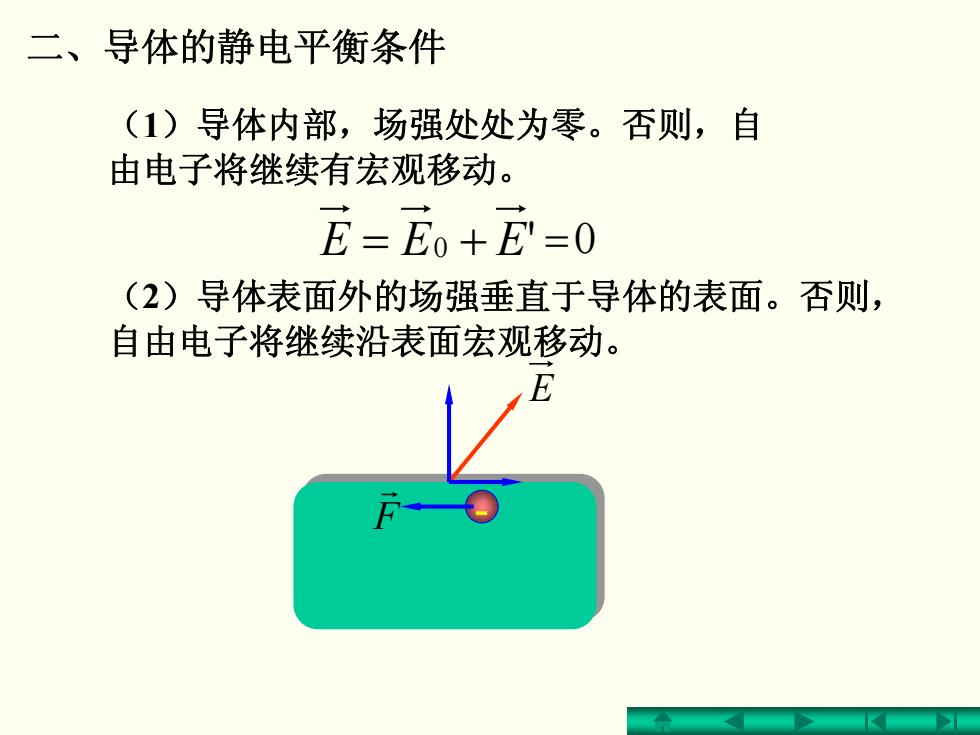
二、导体的静电平衡条件 (1)导体内部,场强处处为零。否则,自 由电子将继续有宏观移动。 E=E0+E=0 (2)导体表面外的场强垂直于导体的表面。否则, 自由电子将继续沿表面宏观移动
二、导体的静电平衡条件 ( 2)导体表面外的场强垂直于导体的表面。否则, 自由电子将继续沿表面宏观移动。 0 += EEE ' = 0 ( 1)导体内部,场强处处为零。否则,自 由电子将继续有宏观移动。 E F - r

三、导体的电势 在导体上任意两点间的电势差为: 。-k。=-%龙di =0 →U。=U。 (1)E=0, 处于静电平衡时,导体上各点 导体内部; 电势相等; (2)E.di=0, •导体成为等势体,导体表面成为 导体表面。 等势面
= UU ba ∫ ⋅−=− )( )( d ba ab lEVV r r = 0 •处于静电平衡时,导体上各点 电势相等; 在导体上任意两点间的电势差为: • a • b 三、导体的电势 •导体成为等势体,导体表面成为 等势面。 导体内部; E = ,0 )1( r 导体表面。 lE =⋅ ,0d )2( r r

四、导体上电荷的分布 1.电荷只分布在导体表面上,导体内部处处不带电。 在导体内任取一高斯面S,由高斯定理: E.ds-0 →∑g=jodW=0 .高斯面为任意 D=0(导体内部) 导体内部没有净电荷,电荷只能分布在导体表面
1. 电荷只分布在导体表面上,导体内部处处不带电。 =⋅ 0d ∫S SEr r == 0d ∑ ∫ Vq V S ρ 内 在导体内任取一高斯面 S,由高斯定理: Q高斯面为任意 E内 = 0 四、导体上电荷的分布 导体内部没有净电荷,电荷只能分布在导体表面。 S + + + + + + + + + + + + + + + + + + + + E内 = 0 ρ = (导体内部) 0

2.导体表面电荷与导体表面外侧电场的关系 设导体表面上的电荷面密度和表面外侧 电场强度如图所示 E 对如图所示高斯面,应用高斯定理: fE.ds=∫Ed5+ ∫Ed △S 导体 △S △S2+AS3) (外底面) (侧面+内底面) =E△S= o△S 0 0=6E1
σ E⊥ r 导体 2. 导体表面电荷与导体表面外侧电场的关系 ∫ ⋅ S SEr r d ( ) ∫∫ + Δ Δ+Δ ⊥ ⋅+⋅= (外底面) (侧面 内底面) 1 32 d d S SS SESE r r r r = ⊥ ΔSE 0 ε σΔS ≡ 设导体表面上的电荷面密度和表面外侧 电场强度如图所示 对如图所示高斯面,应用高斯定理: n 0 eE r r ε σ ⊥ = = 0E⊥ σ ε S1 r Δ S2 r Δ 3 S r Δ E⊥ r

3.静电平衡下的孤立导体 实验研究导体电荷的 定性分布:其表面处 面电荷密度σ与该表 面曲率有关(如图)。 (1)在导体表面曲率为正值 且较大的地方电荷面密度较 大, (2)在曲率较小部分电荷面密度较小。 >当表面凹进时,曲率为负值,电荷面密度更小
(1)在导体表面曲率为正值 且较大的地方电荷面密度较 大, 3. 静电平衡下的孤立导体 实验研究导体电荷的 定性分布:其表面处 面电荷密度σ与该表 面曲率有关(如图)。 (2)在曲率较小部分电荷面密度较小。 ¾当表面凹进时,曲率为负值,电荷面密度更小