
第22章量子力学基础 §22.1实物粒子的波动性 §22.2波函数及统计解释 §22.3不确定性关系 §22.4薛定谔方程 §22.5力学量算符的本征值问题 §22.6薛定谔方程的应用 §22.7氢原子量子理论 §22.8电子的自旋泡利不相容原理
§22.1 实物粒子的波动性 §22.2 波函数及统计解释 §22.3 不确定性关系 §22.4 薛定谔方程 §22.6 薛定谔方程的应用 §22.5 力学量算符的本征值问题 §22.7 氢原子量子理论 §22.8 电子的自旋 泡利不相容原理 第 22 章 量子力学基础

§22.3不确定性关系 一、位置一动量不确定关系 按照经典波动理论,约束在空间某区域内的波不可 能是单色的—不可能具有唯一的波长。 这一结论对物质波同样正确:被束缚在某区域的粒 子不可能具有确定的动量,即粒子的坐标和动量不 能同时取确定值,存在一个不确定关系。 海森堡(W.Heisenberg)在1927年发表了著名的位 置一动量不确定关系 △x·△px~h 以电子的单缝衍射为例说明。电子的单缝衍射“中 央亮纹”半角宽度满足:
§22.3 不确定性关系 按照经典波动理论,约束在空间某区域内的波不可 能是单色的——不可能具有唯一的波长。 这一结论对物质波同样正确:被束缚在某区域的粒 子不可能具有确定的动量,即粒子的坐标和动量不 能同时取确定值,存在一个不确定关系。 海森堡(W. Heisenberg)在1927年发表了著名的位 置—动量不确定关系 hpx Δ ⋅ Δ x ~ 以电子的单缝衍射为例说明。电子的单缝衍射“中 央亮纹”半角宽度满足: 一、位置—动量不确定关系
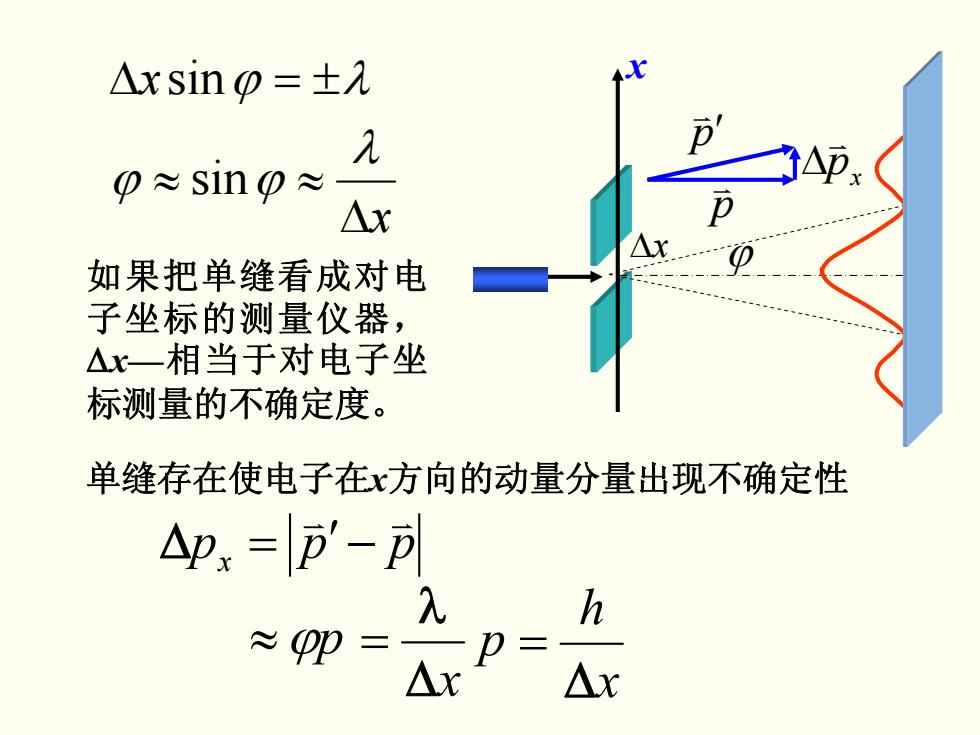
△xsin0=±入 p≈Sln0≈ △x 如果把单缝看成对电 子坐标的测量仪器, △x一相当于对电子坐 标测量的不确定度。 单缝存在使电子在x方向的动量分量出现不确定性 △p.=p'-p 入 h ≈p= △x
pppx v v Δ = ′− ≈ ϕp p Δx λ = x h Δ = 如果把单缝看成对电 子坐标的测量仪器, Δx—相当于对电子坐 标测量的不确定度。 Δx ϕ x p ′ v p v px v Δ 单缝存在使电子在x方向的动量分量出现不确定性 Δx sinϕ = ±λ Δx ≈≈ λ sinϕϕ

△x·△px=h 对坐标x测量得越精确(△越小),动量不确定性 △p就越大(衍射越厉害)。 电子的坐标和动量不能同时确定。 不限制电子坐标时,动量可以取确定值。 严格的不确定性关系应该是: △x·△px≥h/2 Ay·△py≥h/2 Az·△p.≥h/2
hpx ⋅ΔΔ x = 对坐标 x 测量得越精确(Δx 越小),动量不确定性 Δpx就越大(衍射越厉害)。 不限制电子坐标时,动量可以取确定值。 电子的坐标和动量不能同时确定。 严格的不确定性关系应该是: ⎪⎩ ⎪⎨⎧ ≥Δ⋅Δ ≥Δ⋅Δ ≥Δ⋅Δ 2 2 2 h h h z y x pz py px

[例22-21氢氖激光器发光波长入=632.8nm, 谱线宽度△入=10-9nm,求即相干长度, 解:当这种光子沿x方向传播时,它的x坐标的不确 定就是即相干长度,也就是波列长度 谱线展宽导致光子动量的不确定 h h △px= △入 2 .p 杭 2 2 ∴.△x = 2 △X≈ =400km △兄
[例22-2] 氦氖激光器发光波长 λ = 632 8nm . , 谱线宽度 Δλ = 10 nm −9 , 求即相干长度, λ h λ Q p = λ Δ=Δ 2h px λ λ λ λ Δ ≈ Δ = Δ ∴ =Δ 2 2 px 42 π x h 谱线展宽导致光子动量的不确定 解:当这种光子沿 x 方向传播时,它的 x坐标的不确 定就是即相干长度,也就是波列长度 km400 2 = Δ ≈Δ λ λ x

二、能量和时间的不确定关系 将上例激光光子位置一动量不确定性关系 △Ax·Apx≥h/2 变为 同样可得粒子处于某状态的能量和时间的不确定性 关系 △E·△t≥h/2
将上例激光光子位置 —动量不确定性关系 Δ ⋅ ΔtE ≥ h 2 二、能量和时间的不确定关系 Δ ⋅ Δ ≥ h 2 x px 同样可得粒子处于某状态的能量和时间的不确定性 关系 变为 ⎟ ≥ h 2 ⎠ ⎞ ⎜ ⎝ ⎛ Δ⋅Δ c h tc ν
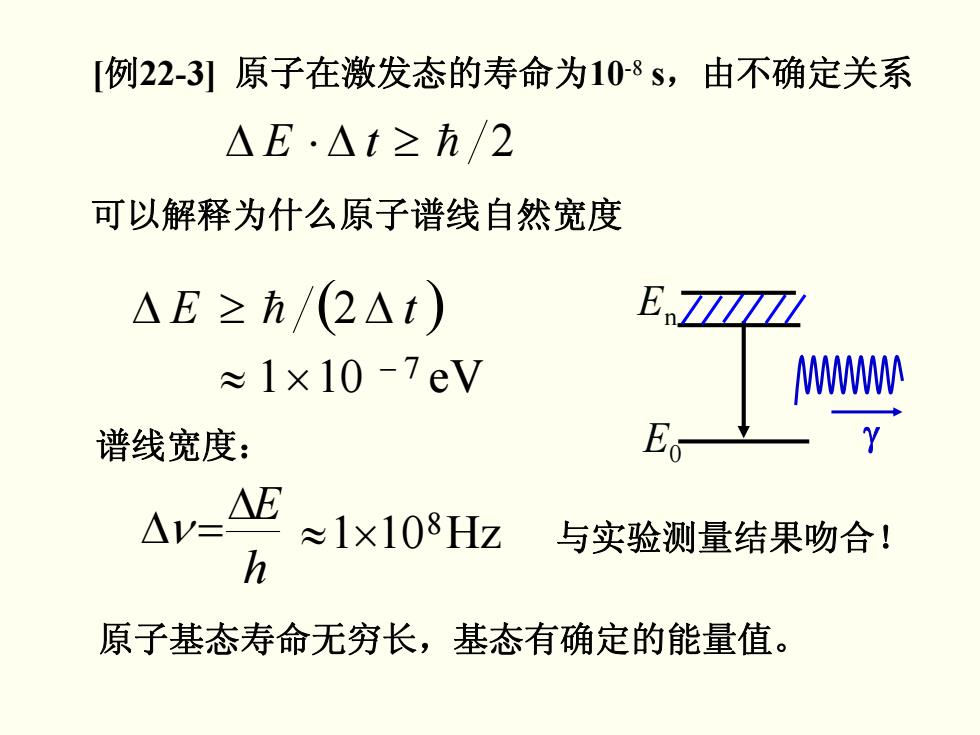
例22-3引原子在激发态的寿命为10-8s,由不确定关系 △E·△t≥h/2 可以解释为什么原子谱线自然宽度 △E≥五/(2△t) ETLA ≈1×10-7eV MM 谱线宽度: Eo AV-AB ≈1×108Hz 与实验测量结果吻合! h 原子基态寿命无穷长,基态有确定的能量值
可以解释为什么原子谱线自然宽度 Δ E ⋅Δ t ≥ h 2 Δ E ≥ h (2 Δ t ) eV101 − 7 ≈ × γ E 0 En 谱线宽度: h ΔE ν =Δ Hz101 8 ≈ × 与实验测量结果吻合! 原子基态寿命无穷长,基态有确定的能量值。 [ 例22-3] 原子在激发态的寿命为10-8 s,由不确定关系

说明:·不确定性与测量没有关系,是微观粒子 波一粒二象性的体现。 •不确定性的物理根源是粒子的波动性。 ·不确定性关系限定了使用经典语言的范围和度 「例22-41氢原子中的电子的轨道运动速度为10m/s, 速度的不确定度: △p △v= 之方1≈10m/s,△wy m 2m△x 可见波动性十分明显,不能用轨道概念描述! 但威尔逊云室可看到一条白亮的粒子径迹~104 cm,由此可得: △p~10-28kgm/s但p~10-23kgm/s P>>△p,波动性不是很明显,轨道概念仍适用。 END
•不确定性关系限定了使用经典语言的范围和度 [例22-4] 氢原子中的电子的轨道运动速度为106m/s, 速度的不确定度: •不确定性的物理根源是粒子的波动性。 说明:• 不确定性与测量没有关系,是微观粒子 波—粒二象性的体现。 m p v Δ Δ = Δxm 1 2 h ≥ ,Δv~v 但威尔逊云室可看到一条白亮的粒子径迹~10-4 cm ,由此可得: p>>Δp,波动性不是很明显,轨道概念仍适用。 m/skg10~ 28 ⋅ − Δp m/skg10~ 23 ⋅ − 但 p m/s106 ≈ 可见波动性十分明显,不能用轨道概念描述! END