
第4章动量和角动量 §4.1动量定理动量守恒定律 §4.2质心质心运动定理 §4.3碰撞问题 §4.4火箭飞行基本原理 §4.5质点的角动量角动量守恒定律 §4.6质点系的角动量
第 4 章 动量和角动量 §4.1 动量定理 动量守恒定律 §4.2 质心 质心运动定理 §4.3 碰撞问题 §4.5 质点的角动量 角动量守恒定律 §4.4 火箭飞行基本原理 §4.6 质点系的角动量

§4.6质点系的角动量 一、作用于质点系的力矩 M-∑a,=∑×月 -mg k J 1.重力矩 m,方 Mg=∑氵×(-mgk)=-m i ×gk m Mg=-元×mgk (m=∑m,)
∑ ∑ ×== i ii i i FrMM r r r r 一、作用于质点系的力矩 1. 重力矩 §4.6 质点系的角动量 kg m rm mkgmrM i ii i g ii r r r r r × ⎟⎟⎟⎠⎞ ⎜⎜⎜⎝⎛ −=−×= ∑ ∑ )( = ∑ )( i mm i g kmgrM r r r c ×−= x y O z cr r kmg r − c

2.内力矩 应,=f×方+月×fn =(匠-)×∫=×f,≡0 >质点系内力矩的矢量和为零
2. 内力矩 O ir r j r r ij f r ji f r ij r i r j jijijiij frfrM r r r r r ×+×= fij ≡ 0 ¾ 质点系内力矩的矢量和为零。 ji rr r r r )( ×−= ijij fr r r ×=
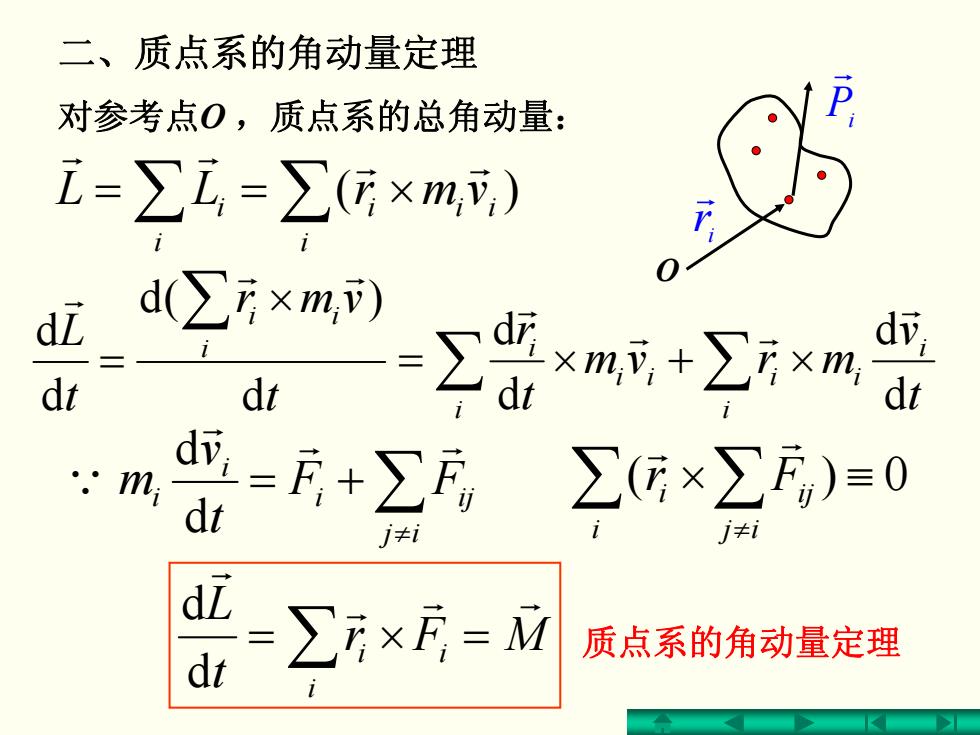
二、质点系的角动量定理 对参考点O,质点系的总角动量: i=∑,=∑(×m,) dL d∑×m) dr dt ∑普m呢+×m号 =F+∑月, mi di ∑(G×∑f)≡0 j≠i d 出一∑万×厅- 质点系的角动量定理
∑ ∑ ×== )( i iii i i vmrLL r r rr 对参考点 O ,质点系的总角动量: O Pi r ir r 二、质点系的角动量定理 t vmr t L i ii d )(d d d ∑ × = r r r ∑≠ += ij i ij i i FF t v m r r r Q d d ∑ ∑ ≡× 0)( ≠ij ij i i Fr r r MFr t L i ii rr r r ∑ =×= d d 质点系的角动量定理 ∑∑ ×+×= i i ii i ii i t v mrvm t r d d d d r rr r

若 M=∑M, =∑F×万=0, 则 i=∑i=工— 质点系角动量守恒定律 d正 ∑F×F=M 质点系的角动量定理
= ∑ i MM i r r LLL 0 i i r r r ∑ == ——质点系角动量守恒定律 若 则 MFr t L i ii rr r r ∑ =×= dd 质点系的角动量定理 ∑ =×= ,0 i Fr ii r r

解释天体系统的旋转盘状结构: 引力 惯性离心力 美国宇航局在地面拍摄的银河系 的侧面,中央是银核
美国宇航局在地面拍摄的银河系 的侧面,中央是银核。 引力 惯性离心力 解释天体系统的旋转盘状结构:

这是银河系外的M83星系,它的形状与 大小和我们的银河系非常相似。 EnD
这是银河系外的M83星系,它的形状与 大小和我们的银河系非常相似。 END