
第5章刚体力学基础 §5.1刚体运动的描述 §5.2刚体的定轴转动定理 §5.3刚体的转动惯量 §5.4刚体定轴转动的角动量守恒定律 §5.5刚体定轴转动的功能原理 §5.6回转仪进动 §5.7刚体的平面运动
第 5 章 刚体力学基础 §5.1 刚体运动的描述 §5.2 刚体的定轴转动定理 §5.3 刚体的转动惯量 §5.4 刚体定轴转动的角动量守恒定律 §5.5 刚体定轴转动的功能原理 §5.6 回转仪 进动 §5.7 刚体的平面运动

§5.4刚体定轴转动的角动量守恒定律 定轴转动角动量定理:M= d(Jo) dt 当M=0时,有 d(Jo) 0 即J0=J00(常量) 定轴转动角动量守恒定律:刚体在定轴转动中,当 对转轴的合外力矩为零时,刚体对转轴的角动量保 持不变。 适用于刚体,非刚体和物体系
定轴转动角动量定理: ( ) t J M d d ω = 定轴转动角动量守恒定律:刚体在定轴转动中,当 对转轴的合外力矩为零时,刚体对转轴的角动量保 持不变。 适用于刚体,非刚体和物体系。 §5.4 刚体定轴转动的角动量守恒定律 M 0= ( ) 0 。 d d = t Jω 当 时, 有 ω ω00 即 = JJ (常量 )
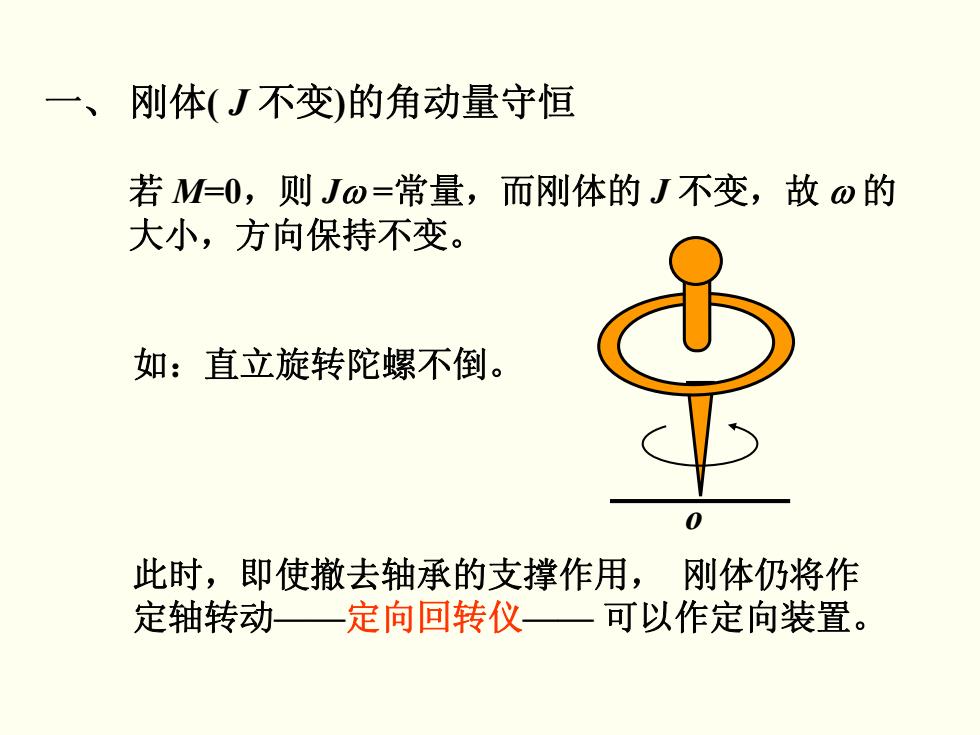
一、 刚体(J不变)的角动量守恒 若M=O,则Jo=常量,而刚体的J不变,故o的 大小,方向保持不变。 如:直立旋转陀螺不倒。 此时,即使撤去轴承的支撑作用,刚体仍将作 定轴转动一定向回转仪一可以作定向装置
一、 刚体( J 不变)的角动量守恒 若 M=0,则 Jω =常量,而刚体的 J 不变,故 ω 的 大小,方向保持不变。 如:直立旋转陀螺不倒。 此时,即使撤去轴承的支撑作用, 刚体仍将作 定轴转动——定向回转仪—— 可以作定向装置。 o

二、非刚体(J可变)的角动量守恒 J0=J0。=常量 当J增大,o就减小,当J减小,o就增大。 如:芭蕾舞,花样滑冰中的转动, 恒星塌缩(R,)→(R,@)中子星 的形成等
二、非刚体( J 可变)的角动量守恒 当 J 增大,ω 就减小,当 J 减小,ω 就增大。 ω = JJ ω00 = 常量 如:芭蕾舞,花样滑冰中的转动, 恒星塌缩 (R0,ω0) → (R,ω) 中子星 的形成等
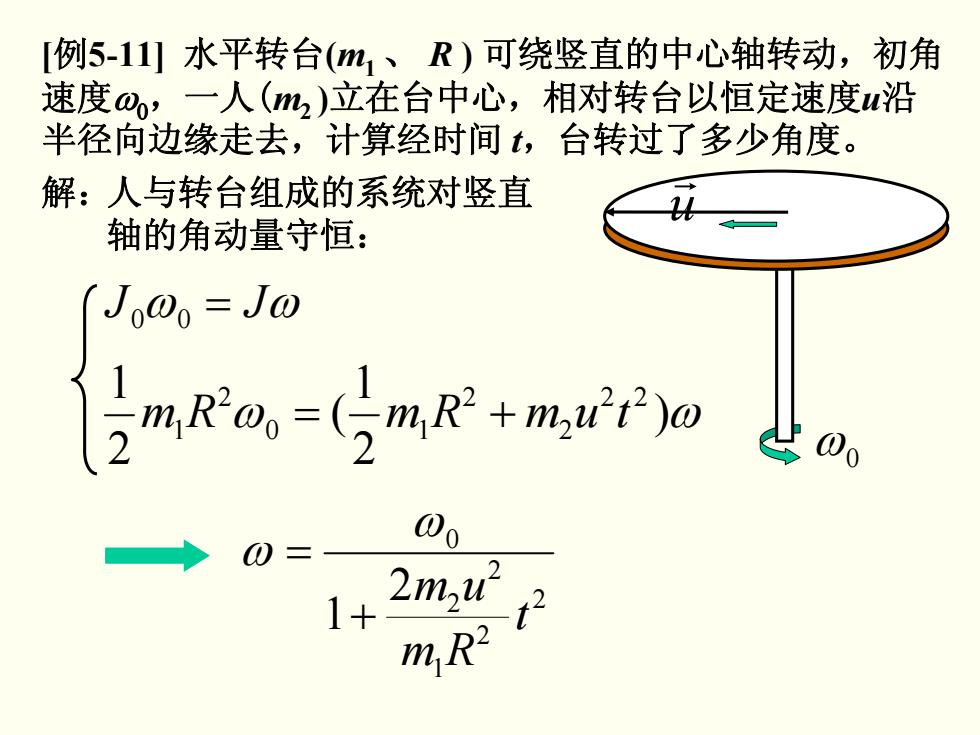
[例5-11]水平转台(m1、R)可绕竖直的中心轴转动,初角 速度@,一人(m2)立在台中心,相对转台以恒定速度u沿 半径向边缘走去,计算经时间,台转过了多少角度。 解:人与转台组成的系统对竖直 轴的角动量守恒: J00=J0 jmR@o=(-mR+mawt)@ 0=- 2mu 1+ 3 mR2
r u ω0 人与转台组成的系统对竖直 轴的角动量守恒: ω00 = JJ ω ω ) ω 2 1 ( 2 1 22 2 2 0 1 2 1 += tumRmRm 2 2 1 2 2 0 2 1 t Rm um + = ω ω [ 例5-11] 水平转台 ( m1 、 R ) 可绕竖直的中心轴转动,初角 速度 ω0,一人( m2 )立在台中心,相对转台以恒定速度 u 沿 半径向边缘走去,计算经时间 t,台转过了多少角度。 解:

台转过的角度: p=∫do=o m 2m22 arctan 22)2 R
∫∫ == t t 0ωϕϕ dd 台转过的角度: ⎥⎥⎥⎥⎦⎤ ⎢⎢⎢⎢⎣⎡ = Rmm ut mm u R 2/1 12 2/1 120 ) 2( arctan ) 2( ω

三、物体系的角动量守恒 若系统由几个物体组成,当系统受到的外力对轴的 力矩的矢量和为零,则系统的总角动量守恒: ∑J,@,=常量 如:直升机机尾加侧向旋叶,是为防止机身的反转
三、物体系的角动量守恒 若系统由几个物体组成,当系统受到的外力对轴的 力矩的矢量和为零,则系统的总角动量守恒: ∑ = 常量 i ii J ω 如:直升机机尾加侧向旋叶,是为防止机身的反转

[例5-12]】摩擦离合器飞轮1:J1、o摩擦轮2:J2静 止,两轮沿轴向结合,结合后两轮达到的共同角速度。 解:两轮对共同转轴的角动量守恒 J10,=(J1+J2)0 ]片 J1@1 (J1+J2) 试与下例的齿轮啮合过程比较
[例5-12] 摩擦离合器 飞轮1:J1、 ω1 摩擦轮2: J2 静 止,两轮沿轴向结合,结合后两轮达到的共同角速度。 两轮对共同转轴的角动量守恒 ω = ( + JJJ 2111 )ω ( ) 21 11 JJ J + = ω ω 解: 试与下例的齿轮啮合过程比较。 2 1 ω1 2 1 ω
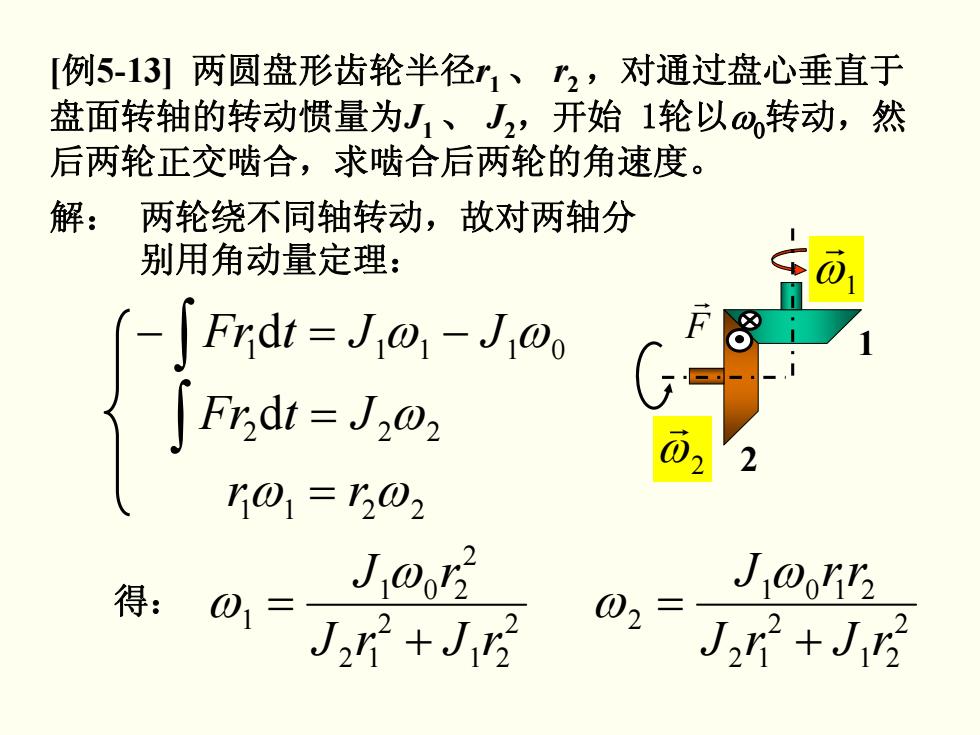
[例5-13]两圆盘形齿轮半径r1、了2,对通过盘心垂直于 盘面转轴的转动惯量为J1、J2,开始1轮以0,转动,然 后两轮正交啮合,求啮合后两轮的角速度。 解:两轮绕不同轴转动,故对两轴分 别用角动量定理: (-JFrdt=J@,-J@o Fndt=J2@ 01=1302 得: J103 J03 0=J+J5 0,=J,+J5
[例5-13] 两圆盘形齿轮半径r1 、 r2 ,对通过盘心垂直于 盘面转轴的转动惯量为J1 、 J2,开始 1轮以ω0转动,然 后两轮正交啮合,求啮合后两轮的角速度。 两轮绕不同轴转动,故对两轴分 别用角动量定理: ∫ 1 −=− 0111 d JJtFr ωω ∫ 2 = 22 d JtFr ω ω ω2211 = rr 得: 2 21 2 12 2 201 1 rJrJ rJ + = ω ω 2 21 2 12 2101 2 rJrJ rrJ + = ω ω 解: ω0 r 1 ω2 2 r F r ω1 r

[例5-14均质细棒:m、1,水平轴O,小球:m,与棒 相碰,碰前V碰后如图,设碰撞时间很短,棒保 持竖直,求碰后棒的角速度。 解:系统对O轴角动量守恒 mly =ml-@-m,lv' 3,(y+v) ml 注意:系统总动量一般不守恒,因为轴承处的外力不能忽略。 只当碰撞在打击中心时,N=0,系统的水平动量守恒: m2v =mve-mv=mla-mv (m2号w=3m,l20-m2号1w') END
[例5-14] 均质细棒:m1、 l ,水平轴O,小球:m2与棒 相碰,碰前 碰后 如图,设碰撞时间很短,棒保 持竖直,求碰后棒的角速度。 v r v ′ r 系统对O轴角动量守恒 2 2 3 1 1 2 ω −= vlmlmlvm ′ ( ) lm vvm 1 2 3 + ′ ω = 注意:系统总动量一般不守恒,因为轴承处的外力不能忽略。 只当碰撞在打击中心时,Nx=0,系统的水平动量守恒: 解: −= ′ −= vmlmvmvmvm ′ 2 1 2 1 2c12 ω 3 2 2 2 3 1 1 3 2 2 ( ω −= vlmlmlvm ′) r v v ′ r O ω END